Halvcirkel hvordan man beregner omkrets, areal, sentroid, øvelser

De halvsirkel er en plan figur avgrenset av en diameter på omkretsen og en av de to flate sirkelbuer bestemt av nevnte diameter.

På denne måten grenser en halvcirkel av en halvkrets, som består av en flat sirkelbue og et rett segment som forbinder endene av den flate sirkelbuen. Halvsirkelen omfatter halvsirkelen og alle punkter i den..

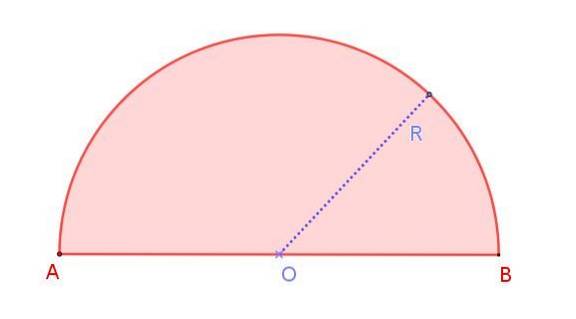
Vi kan se dette i figur 1, som viser en halvsirkel med radius R, hvis mål er halvparten av diameteren AB. Merk at i motsetning til en sirkel der det er uendelige diametre, er det bare en diameter i halvkretsen.

Halvsirkelen er en geometrisk figur med mange bruksområder innen arkitektur og design, som vi ser på følgende bilde:

Artikkelindeks

• 1 Elementer og mål på en halvcirkel
  • 1.1 Omkrets av en halvcirkel
  • 1.2 Område av en halvcirkel
  • 1.3 Midroid av en halvcirkel
  • 1.4 Treghetsmoment for en halvcirkel
  • 1.5 Innskrevet vinkel
• 2 Løst øvelser
  • 2.1 Øvelse 1 
  • 2.2 Øvelse 2
  • 2.3 Øvelse 3
  • 2.4 Øvelse 4
  • 2.5 Øvelse 5
• 3 Referanser

Elementer og mål på en halvcirkel

Elementene i en halvcirkel er:

1.- Flyet sirkelbue A⌒B

2.- Segmentet [AB] 

3.- Punktene i halvsirkelen sammensatt av buen A⌒B og segmentet [AB].

Omkrets av en halvcirkel

Omkretsen er summen av buens kontur pluss den for det rette segmentet, derfor:

Perimeter = buelengde A⌒B + segmentlengde [AB]

Når det gjelder en halvsirkel med radius R, vil omkretsen P bli gitt av formelen:

P = π⋅R + 2⋅R = (π + 2) ⋅R

Den første termen er halv omkretsen av en sirkel med radius R, mens den andre er lengden på diameteren, som er dobbelt så stor som radiusen..

Område av en halvcirkel

Siden en halvcirkel er en av de plane vinkelsektorene som gjenstår når en tegner en diameter gjennom omkretsen, vil arealet A være halvparten av arealet av sirkelen som inneholder halvsirkelen med radius R:

A = (π⋅R^to) / 2 = ½ π⋅R^to

Midroid av en halvcirkel

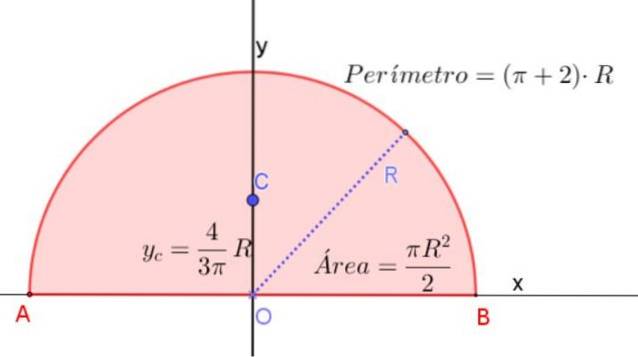
Midroiden til en halvcirkel er på symmetriaksen i en høyde målt fra diameteren 4 / (3π) ganger radien R.

Dette tilsvarer omtrent 0,424⋅R, målt fra midten av halvcirkelen og på symmetriaksen, som vist i figur 3.

Treghetsmoment av en halvcirkel

Treghetsmomentet til en plan figur i forhold til en akse, for eksempel x-aksen, er definert som:

Integralet av kvadratet til avstanden til punktene som tilhører figuren til aksen, og integrasjonsdifferensialet er et uendelig minimum av element, tatt ved posisjonen til hvert punkt. 

Figur 4 viser definisjonen av treghetsmomentet I_x av halvsirkelen med radius R, med hensyn til X-aksen som passerer gjennom sin diagonale:

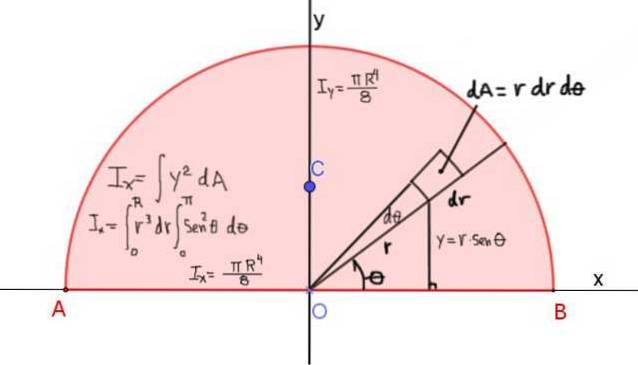
Treghetsmomentet rundt x-aksen er gitt av:

Jeg_x = (π⋅R⁴) / 8

Og treghetsmomentet i forhold til symmetriaksen y er:

Iy = (π⋅R⁴) / 8

Det bemerkes at begge treghetsmomentene faller sammen i formelen, men det er viktig å merke seg at de refererer til forskjellige akser.

Innskrevet vinkel

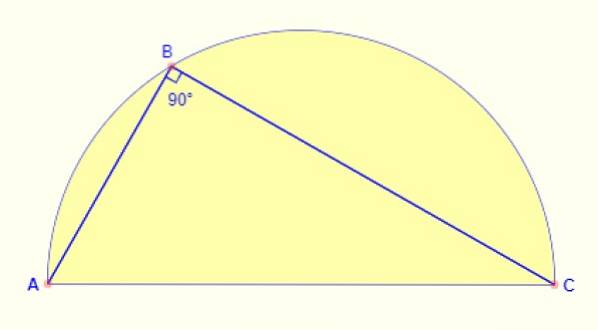
Vinkelen påskrevet i halvcirkelen er alltid 90º. Uansett hvor punktet blir tatt på buen, er vinkelen som er dannet mellom sidene AB og BC på figuren alltid riktig..

Løst øvelser

Øvelse 1 

Bestem omkretsen til en halvsirkel med en radius på 10 cm.

Løsning

Husk at omkretsen som en funksjon av radius er gitt av formelen vi så tidligere:

P = (2 + π) ⋅R

P = (2 + 3,14) ⋅ 10 cm = 5,14 ⋅ 10 cm = 51,4 cm.

Øvelse 2

Finn området til en halvcirkel med en radius på 10 cm.

Løsning

Formelen for området til en halvcirkel er:

A = ½ π⋅R^to = ½ π⋅ (10cm)^to = 50π cm^to = 50 x 3,14 cm^to = 157 cm^to.

Øvelse 3

Bestem høyden h på midtsiden av en halvsirkel med radius R = 10 cm målt fra basen, og halvcirkelens diameter er den samme. 

Løsning

Centroid er likevektspunktet til halvcirkelen og dens posisjon er på symmetriaksen i en høyde h fra basen (halvcirkelens diameter):

h = (4⋅R) / (3π) = (410 cm) / (3 x 3,14) = 4,246 cm

Øvelse 4

Finn treghetsmomentet til en halvcirkel i forhold til aksen som sammenfaller med diameteren, vel vitende om at halvsirkelen er laget av et tynt ark. Radien er 10 cm og massen er 100 gram.

Løsning

Formelen som gir treghetsmomentet til halvcirkelen er:

Jeg_x = (π⋅R⁴) / 8

Men siden problemet forteller oss at det er en materiell halvcirkel, må den forrige relasjonen multipliseres med overflatetettheten av massen til halvcirkelen, som vil bli betegnet med σ.

Jeg_x = σ (π⋅R⁴) / 8

Vi fortsetter deretter med å bestemme σ, som ikke er noe annet enn halvcirkelens masse delt på arealet.

Området ble bestemt i øvelse 2 og resultatet var 157 cm^to. Da vil overflatetettheten til denne halvsirkelen være:

σ = 100 gram / 157 cm^to = 0,637 g / cm^to

Da beregnes treghetsmomentet med hensyn til diameteren slik:

Jeg_x = (0,637 g / cm^to) [3,1416 ⋅ (10 cm)⁴] / 8

Resultat:

Jeg_x = 2502 g⋅cm^to

Øvelse 5

Bestem treghetsmomentet til en halvsirkel med en radius på 10 cm laget av et materialark med en overflatetetthet på 0,637 g / cm^to langs en akse som passerer gjennom dens midroid og er parallell med diameteren.

Løsning

For å løse denne øvelsen er det nødvendig å huske Steiners teorem om treghetsmomenter av parallelle akser, som sier:

Treghetsmomentet I med hensyn til en akse som er i en avstand h fra sentroid er lik summen av treghetsmomentet I_c med hensyn til en akse som passerer gjennom sentroid og er parallell med det første pluss produktet av massen ganger kvadratet for skillet mellom de to aksene.

Jeg = jeg_c + M h^to

I vårt tilfelle er jeg kjent som er treghetsmomentet med hensyn til diameteren, som allerede var beregnet i øvelse 4. Skillet h mellom diameteren og sentroid er også kjent, som ble beregnet i øvelse 3.

Vi trenger bare å fjerne Ic:

Jeg_c = I - M h^to

Jeg_c = 2502 g⋅cm^to - 100g 4.2 (4,246 cm)^to gir som et resultat at treghetsmomentet gjennom en akse parallell med diameteren og passerer gjennom sentroid er: 

Jeg_c = 699,15 g⋅cm^to

Referanser

1. Alexander, D. 2013. Geometri. 5. Utgave. Cengage læring.
2. Math Open Reference. Halvsirkel. Gjenopprettet fra: mathopenref.com.
3. Universe Formler Halvsirkel. Gjenopprettet fra: universoformulas.com.
4. Universumsformler. Område av en halvcirkel. Gjenopprettet fra: universoformulas.com.
5. Wikipedia. Halvsirkel. Gjenopprettet fra: en.wikipedia.com.