
Sentrale symmetriegenskaper, eksempler og øvelser
To punkter A og A har sentral symmetri med hensyn til et punkt O når segmentet AA 'passerer gjennom det og også er midtpunktet til AA'. Punkt O kalles sentrum for symmetri.
Den sentrale symmetriske delen av en trekant ABC i forhold til et punkt O, er en annen trekant A'B'C 'som har følgende egenskaper:
-Homologe segmenter er like lange
-De tilsvarende vinklene deres har samme mål.
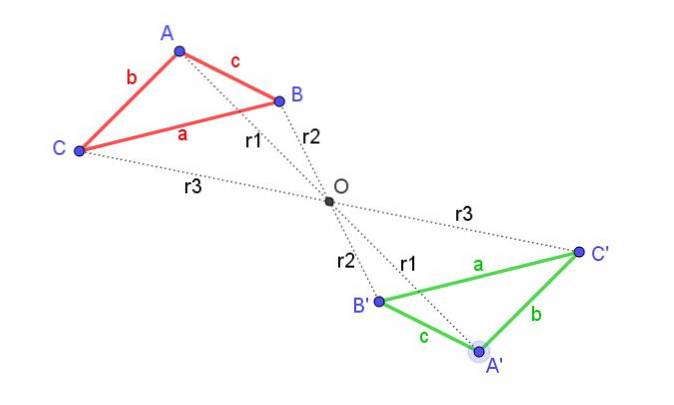
I figur 1 kan du se en trekant ABC (rød) og dens sentrale symmetri A'B'C '(grønn), i forhold til sentrum av symmetri O.
I samme figur vil en oppmerksom observatør innse at det samme resultatet oppnås ved å bruke en rotasjon av den opprinnelige trekanten, så lenge den er 180 ° og er sentrert i O.
Derfor tilsvarer en sentral symmetri en 180 ° sving i forhold til sentrum av symmetri.
Artikkelindeks
- 1 Egenskaper for sentral symmetri
- 2 Eksempler
- 2.1 Eksempel 1
- 2.2 Eksempel 2
- 3 Løst øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 4 Referanser
Egenskaper for sentral symmetri
En sentral symmetri har følgende egenskaper:
-Sentrum av symmetri er midtpunktet i segmentet som forbinder et punkt med sin symmetri.
-Et symmetrisk punkt av et annet som ligger i sentrum av symmetri, sammenfaller med sentrum for symmetri.
-Den sentrale symmetriske delen av en trekant er en trekant kongruent (lik) med originalen.
-Bildet ved en sentral symmetri av en sirkel er en annen sirkel med lik radius.
-En sirkel har sentral symmetri om sitt eget sentrum.

-Ellipsen har sentral symmetri om sentrum.
-Et segment har sentral symmetri om midtpunktet.
-Den ligesidige trekanten har ikke sentral symmetri i forhold til sentrum, fordi symmetrien, selv om den er kongruent til den første, gir en rotert liksidig trekant.
-Kvadrater har sentral symmetri om sentrum.
-En femkant mangler sentral symmetri om sentrum.
-Vanlige polygoner har sentral symmetri når de har et jevnt antall sider.
Eksempler
Symmetri-kriterier har mange anvendelser innen naturvitenskap og ingeniørfag. Sentral symmetri er til stede i naturen, for eksempel har iskrystaller og spindelvev denne typen symmetri.
Videre blir mange problemer lett løst når eksistensen av sentral symmetri og andre typer symmetri blir utnyttet. Derfor er det praktisk å raskt identifisere når det oppstår.

Eksempel 1
Gitt et punkt P med koordinater (a, b), må vi finne koordinatene til dets symmetriske P 'med hensyn til opprinnelsen O til koordinatene (0, 0).
Det første er å konstruere punktet P ', for hvilket en linje tegnes som går gjennom opprinnelsen O og gjennom punktet P. Ligningen til linjen er y = (b / a) x.
La oss kalle (a ', b') koordinatene til det symmetriske punktet P '. Punktet P 'må ligge på linjen som går gjennom O og derfor er det sant: b' = (b / a) a '. Videre må avstanden OP være lik OP ', som i analytisk form skrives slik:
√ (tilto + bto) = √ (a 'to + b 'to )
Følgende er å erstatte b '= [(b / a) .a'] i ovennevnte uttrykk og kvadratere begge sider av likheten for å eliminere kvadratroten: (ato + bto) = [a 'to + (bto/tilto).til'to]
Ved å trekke ut felles faktor og forenkle, får vi det en 'to = ato. Denne ligningen har to virkelige løsninger: a '= + a eller a' = -a.
For å få b ', bruker vi igjen b' = (b / a) a '. Hvis den positive løsningen på a 'er erstattet, kommer vi til at b' = b. Og når den negative løsningen er erstattet, så er b '= -b.
Den positive løsningen gir for P 'samme punkt P, så det kastes. Den negative løsningen gir definitivt koordinatene til det symmetriske punktet:
P ': (-a, -b)
Eksempel 2
Det kreves å vise at et segment AB og dets sentrale symmetriske A'B 'har samme lengde.
Starter med koordinatene til punkt A, som er (Ax, Ay) og de for punkt B: (Bx, By), blir lengden på segment AB gitt av:
d (AB) = √ ((Bx - Ax)to + (Av - Ay)to )
Analogisk vil det symmetriske segmentet A'B 'ha lengden gitt av:
d (A'B ') = √ ((Bx' - Ax ')to + (Av '- Ay')to )
Koordinatene til det symmetriske punktet A 'er Ax' = -Ax og Ay '= -Ay. Tilsvarende er de av B 'Bx' = -Bx og By '= -By. Hvis disse koordinatene er substituert i ligningen til avstanden d (A'B ') har vi:
d (A'B ') = √ ((-Bx + Ax)to + (-By + Ay)to) som tilsvarer:
√ ((Bx - Ax)to + (Av - Ay)to) = d (AB)
Dermed blir vist at begge segmentene har samme lengde.
Løst øvelser
- Øvelse 1
Vis analytisk at den sentrale symmetriske O i en sirkel med radius R og sentrum O er den samme originale sirkelen.
Løsning
Ligningen til en sirkel med radius R og sentrum O (0,0) er:
xto + Yto = Rto (Likning av omkrets C)
Hvis det ved hvert punkt P av omkretsen y av koordinatene (x, y) er funnet den symmetriske P 'av koordinatene (x', y '), er ligningen for den symmetriske omkretsen:
x 'to + Y 'to = Rto (Ligning av den symmetriske sirkelen C ')
Nå refererer vi til resultatet av eksempel 1, der det konkluderes med at koordinatene til et punkt P ', symmetrisk til P og med koordinatene (a, b), er (-a, -b).
Men i denne øvelsen har punkt P koordinater (x, y), så dets symmetriske P 'vil ha koordinater x' = -x og y '= -y. Ved å erstatte dette i ligningen til den symmetriske sirkelen har vi:
(-x)to + (-Y)to = Rto
Som tilsvarer: xto+ Yto = Rto, konkluderer med at den sentrale symmetriske av en sirkel med hensyn til sentrum er omkretsen i seg selv.
- Øvelse 2
Vis geometrisk at sentral symmetri bevarer vinkler.
Løsning
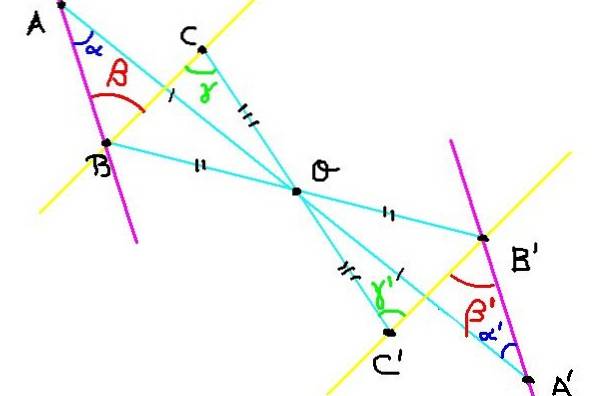
Det er tre punkter A, B og C på flyet. Dens symmetri A ', B' og C 'er konstruert i forhold til sentrum av symmetri O, som vist i figur 4.
Nå må vi vise at vinkelen ∡ABC = β har samme mål som vinkelen ∡A'B'C '= β'.
Siden C og C 'er symmetriske, så er OC = OC'. Tilsvarende OB = OB 'og OA = OA'. På den annen side er vinkelen ∡BOC = ∡B'OC 'fordi de står i motsetning til toppunktet.
Deretter er trekantene BOC og B'OC 'kongruente fordi de har lik vinkel mellom to like sider.
Siden BOC er kongruent til B'OC 'så er vinklene γ Y γ ' De er like. Men disse vinklene, i tillegg til å oppfylle γ = γ ' er interne vekslinger mellom linjene BC og B'C 'som antyder at linjen BC er parallell med B'C'.
På samme måte er BOA kongruent til B'OA 'som det følger at α = α ' . Men α Y α ' er alternative innvendige vinkler mellom linjene BA og B'A ', hvorfra det konkluderes med at linjen BA er parallell med B'A'.
Siden vinkelen ∡ABC = β har sidene parallelle med vinkelen ∡A'B'C '= β' og begge er akutte, konkluderes det med at:
∡ABC = ∡A'B'C '= β = β'
Beviser på denne måten at den sentrale symmetrien bevarer målene for vinklene.
Referanser
- Baldor, J. A. 1973. Plane and Space Geometry. Mellomamerikansk kultur.
- Matematiske lover og formler. Vinkelmålesystemer. Gjenopprettet fra: ingemecanica.com.
- Wentworth, G. Plane Geometry. Gjenopprettet fra: gutenberg.org.
- Wikipedia. Sentral symmetri. Gjenopprettet fra: es.wikipedia.com
- Wikipedia. Transportør. Gjenopprettet fra: es.wikipedia.com
- Zapata F. Konjugere indre og ytre vinkler. Gjenopprettet fra: lifeder.com



Ingen har kommentert denne artikkelen ennå.