
Oktal systemhistorikk, nummereringssystem, konverteringer
De oktalt system er et base-åtte (8) posisjoneringsnummereringssystem; det vil si at den består av åtte sifre, som er: 0, 1, 2, 3, 4, 5, 6 og 7. Derfor kan hvert siffer i et oktaltall ha en hvilken som helst verdi fra 0 til 7. De oktale tallene dannes fra binære tall.
Dette skyldes at basen har en nøyaktig styrke på to (2). Det vil si at tallene som tilhører det oktale systemet dannes når de grupperes i tre påfølgende sifre, ordnet fra høyre til venstre, og dermed oppnår desimalverdien..

Artikkelindeks
- 1 Historie
- 2 Oktalt nummereringssystem
- 3 Konvertering fra oktalt til desimalt system
- 3.1 Eksempel 1
- 3.2 Eksempel 2
- 4 Konvertering fra desimal til oktalt system
- 4.1 Eksempel
- 5 Konvertering fra oktalt til binært system
- 6 Konvertering fra binært til oktalt system
- 7 Konvertering fra oktal til heksadesimal og omvendt
- 7.1 Eksempel
- 8 Referanser
Historie
Det oktale systemet har sin opprinnelse i eldgamle tider, da folk brukte hendene sine til å telle dyr fra åtte til åtte.
For eksempel, for å telle antall kyr i en stall, begynte man å telle med høyre hånd og ble med tommelen med lillefingeren; for å telle det andre dyret ble tommelen satt sammen med pekefingeren, og så videre med de resterende fingrene på hver hånd, til den fullførte 8.
Det er muligheten for at i det gamle ble det oktale nummereringssystemet brukt før desimal for å kunne telle interdigital mellomrom; dvs. telle alle fingrene unntatt tommelen.
Senere ble det oktale nummereringssystemet etablert, som stammer fra det binære systemet, fordi det trenger mange sifre for å representere bare ett tall; fra da av ble det oktale og sekskantede system opprettet, som ikke krever så mange sifre og lett kan konverteres til det binære systemet.
Oktalt nummereringssystem
Det oktale systemet består av åtte sifre som går fra 0 til 7. Disse har samme verdi som i tilfellet med desimalsystemet, men deres relative verdi endres avhengig av posisjonen de inntar. Verdien av hver posisjon er gitt av kreftene til base 8.
Sifretes posisjon i et oktalt tall har følgende vekter:
84, 83, 8to, 81, 80, oktalt punkt, 8-1, 8-to, 8-3, 8-4, 8-5.
Det største oktale tallet er 7; på denne måten, når man teller i dette systemet, økes posisjonen til et siffer fra 0 til 7. Når 7 er nådd, resirkuleres det til 0 for neste telling; på denne måten økes neste sifferposisjon. For å telle sekvenser vil det i det oktale systemet være:
- 0, 1, 2, 3, 4, 5, 6, 7, 10.
- 53, 54, 55, 56, 57, 60.
- 375, 376, 377, 400.
Det er en grunnleggende setning som brukes på det oktale systemet, og det uttrykkes som følger:
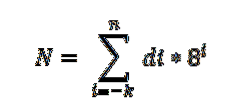
I dette uttrykket representerer di sifferet multiplisert med kraften til base 8, som indikerer stedverdien til hvert siffer, på samme måte som det er ordnet i desimalsystemet.
For eksempel har du tallet 543.2. For å ta det til det oktale systemet, brytes det ned som følger:
N = ∑ [(5 * 8to) + (4 * 81) + (3 *80) + (2 *8-1)] = (5 * 64) + (4 * 8) + (2 * 1) + (2 * 0,125)
N = 320 +32 + 2 + 0,25 = 354 + 0,25d
På den måten må du 543,2hva = 354,25d. Subskriptet q indikerer at det er et oktaltall som også kan representeres av tallet 8; og tegnet d refererer til desimaltallet, som også kan representeres av tallet 10.
Konvertering fra oktalt til desimalt system
For å konvertere et tall fra det oktale systemet til dets ekvivalente i desimalsystemet, trenger du bare å multiplisere hvert oktale siffer med dets stedverdi, fra høyre.
Eksempel 1
7328 = (7* 8to) + (3* 81) + (2* 80) = (7 * 64) + (3 * 8) + (2 * 1)
7328= 448 +24 +2
7328= 47410
Eksempel 2
26.98 = (2 *81) + (6* 80) + (9* 8-1) = (2 * 8) + (6 * 1) + (9 * 0,125)
26.98 = 16 + 6 + 1,125
26.98= 23,12510
Konvertering fra desimal til oktalt system
Et desimaltall kan konverteres til et oktaltall ved å bruke den gjentatte delingsmetoden, der desimaltallet divideres med 8 til kvotienten er lik 0, og resten av hver divisjon vil representere det oktale tallet..
Restene bestilles fra siste til første; det vil si at den første resten vil være det minst signifikante tallet i det oktale tallet. På den måten vil det viktigste tallet være den siste resten..
Eksempel
Oktal av desimalnummer 26610
- Del desimaltallet 266 med 8 = 266/8 = 33 + resten av 2.
- Del deretter 33 med 8 = 33/8 = 4 + resten av 1.
- Del 4 med 8 = 4/8 = 0 + resten av 4.
Siden det med den siste delingen oppnås en kvotient mindre enn 1, betyr det at resultatet er funnet; Du trenger bare å bestille resten omvendt, på en slik måte at det oktale tallet på desimal 266 er 412, som du kan se på følgende bilde:
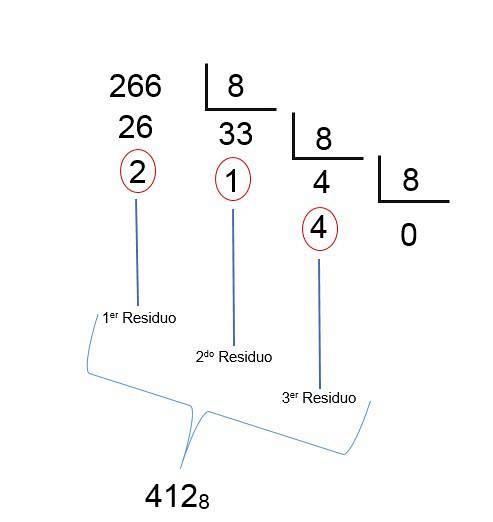
Konvertering fra oktalt til binært system
Konvertering fra oktalt til binært gjøres ved å konvertere det oktale tallet til det tilsvarende binære tallet, bestående av tre sifre. Det er en tabell som viser hvordan de åtte mulige sifrene konverteres:
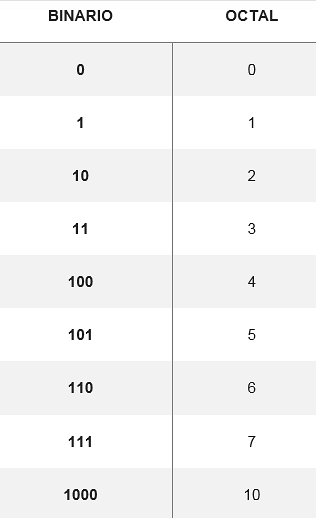
Fra disse konverteringene kan du endre hvilket som helst tall fra det oktale systemet til binært, for eksempel for å konvertere tallet 5728 deres ekvivalenter blir søkt i tabellen. Dermed må den:
58 = 101
78= 111
to8 = 10
Derfor 5728 tilsvarer 10111110 i det binære systemet.
Konvertering fra binær til oktal
Prosessen med å konvertere binære heltall til oktale heltall er den omvendte driften av den forrige prosessen.
Det vil si at biter av det binære tallet er gruppert i to grupper på tre biter, fra høyre til venstre. Deretter gjøres konverteringen fra binær til oktal med forrige tabell.
I noen tilfeller vil det binære tallet ikke ha grupper på 3 biter; for å fullføre den, legges en eller to nuller til venstre for den første gruppen.
Hvis du for eksempel vil endre det binære tallet 11010110 til oktalt, gjør du følgende:
- Grupper på 3 biter dannes fra høyre (siste bit):
11010110
- Siden den første gruppen er ufullstendig, blir et ledende null lagt til:
011010110
- Konverteringen gjøres fra tabellen:
011 = 3
010 = 2
110 = 6
Dermed tilsvarer det binære tallet 011010110 3268.
Konvertering fra oktal til heksadesimal og omvendt
For å endre fra et oktalt tall til det heksadesimale systemet eller fra heksadesimalt til det oktale, er det nødvendig å konvertere tallet til binært først, og deretter til ønsket system.
For dette er det en tabell der hvert heksadesimale siffer er representert med tilsvarende i binærsystemet, sammensatt av fire sifre.
I noen tilfeller vil det binære tallet ikke ha grupper på 4 biter; for å fullføre den, legges en eller to nuller til venstre for den første gruppen
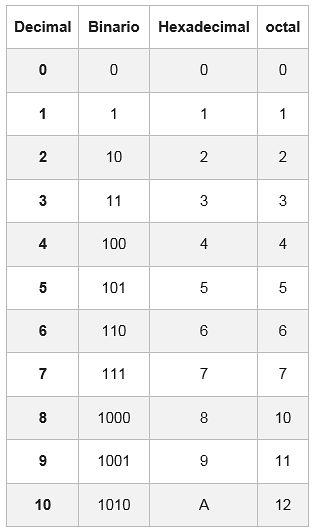
Eksempel
Konverter oktaltall 1646 til heksadesimaltall:
- Konverter tallet fra oktalt til binært
18 = 1
68 = 110
48 = 100
68 = 110
- Dermed 16468 = 1110100110.
- For å konvertere fra binær til heksadesimal, ordnes de først i en gruppe på 4 biter, fra høyre til venstre:
11 1010 0110
- Den første gruppen er fullført med nuller, slik at den kan ha 4 biter:
0011 1010 0110
- Konverteringen er laget fra det binære til heksadesimale systemet. Likhetene erstattes ved hjelp av tabellen:
0011 = 3
1010 = A.
0110 = 6
Dermed tilsvarer oktaltallet 1646 3A6 i det heksadesimale systemet..
Referanser
- Bressan, A. E. (1995). Introduksjon til nummereringssystemer. Argentinsk handelshøyskole.
- Harris, J. N. (1957). Introduksjon til binære og oktale nummereringssystemer: Lexington, Mass. Armed Services Technical Information Agency.
- Kumar, A. A. (2016). Grunnleggende om digitale kretser. Learning Pvt.
- Peris, X. C. (2009). Enkeltoperative systemer.
- Ronald J. Tocci, N. S. (2003). Digitale systemer: prinsipper og applikasjoner. Pearson Education.
Ingen har kommentert denne artikkelen ennå.