
Summen av polynomer, hvordan du gjør det, eksempler, øvelser
De summen av polynomer er operasjonen som består i å legge til to eller flere polynomer, noe som resulterer i et annet polynom. For å utføre det er det nødvendig å legge til vilkårene i samme rekkefølge for hvert av polynomene og indikere den resulterende summen.
La oss først gjennomgå betydningen av "vilkår i samme rekkefølge." Ethvert polynom består av tillegg og / eller subtraksjoner av termer.

Begrepene kan være produkter med reelle tall og en eller flere variabler, representert med bokstaver, for eksempel: 3xto og -√5.atobc3 er vilkår.
Betingelsene for den samme ordren er de som har samme eksponent eller kraft, selv om de kan ha en annen koeffisient.
-Like ordrevilkår er: 5x3, √2 x3 og -1 / 2x3
-Ulike ordrevilkår: -2x-to, 2xy-1 og √6xtoY
Det er viktig å huske på at bare vilkår av samme rekkefølge kan legges til eller trekkes fra, en operasjon kjent som reduksjon. Ellers blir summen bare indikert.
Når begrepet vilkår i samme rekkefølge er avklart, blir polynomene lagt til ved å følge disse trinnene:
-Rekkefølge Først polynomene som skal legges til, alt på samme måte, enten på en økende eller avtagende måte, det vil si med kreftene fra lavere til høyere eller omvendt.
-Å fullføre, i tilfelle strøm mangler i sekvensen.
-Redusere som vilkår.
-Indikerer den resulterende summen.
Artikkelindeks
- 1 Eksempler på tilsetning av polynomer
- 1.1 Legg til to eller flere polynomer med mer enn én variabel
- 2 Øvelser for å legge til polynomer
- 2.1 - Øvelse 1
- 2.2 - Øvelse 2
- 3 Referanser
Eksempler på tilsetning av polynomer
Vi begynner med å legge til to polynomer med en enkelt variabel kalt x, for eksempel polynomene P (x) og Q (x) gitt av:
P (x) = 2xto - 5x4 + 2x -x5 - 3x3 +12
Q (x) = x5- 25 x + xto
Ved å følge trinnene som er beskrevet, begynner du med å bestille dem i synkende rekkefølge, som er den vanligste måten:
P (x) = -x5- 5x4 - 3x3 + 2xto + 2x +12
Q (x) = x5+ xto - 25x
Polynomet Q (x) er ikke komplett, man ser at det mangler krefter med eksponenter 4, 3 og 0. Sistnevnte er ganske enkelt det uavhengige begrepet, det som ikke har noen bokstav.
Q (x) = x5+ 0x4 + 0x3 + xto - 25x + 0
Når dette trinnet er gjort, er de klare til å legge til. Du kan legge til lignende vilkår og deretter indikere summen, eller plassere de bestilte polynomene hverandre og redusere med kolonner på denne måten:
- x5 - 5x4 - 3x3 + 2xto + 2x +12
+ x5 + 0x4 + 0x3 + xto - 25x + 0 +
--
0x5-5x4 - 3x3 +3xto - 23x + 12 = P (x) + Q (x)
Det er viktig å merke seg at når det legges til, gjøres det algebraisk med respekt for tegnregelen, på denne måten 2x + (-25 x) = -23x. Det vil si at hvis koeffisientene har et annet tegn, blir de trukket og resultatet bærer tegnet på det større.
Legg til to eller flere polynomer med mer enn én variabel
Når det gjelder polynomer med mer enn én variabel, blir en av dem valgt for å bestille den. Anta for eksempel at du ber om å legge til:
R (x, y) = 5xto - 4yto + 8xy - 6y3
Y:
T (x, y) = ½ xto- 6yto - 11xy + x3Y
En av variablene er valgt, for eksempel x for å bestille:
R (x, y) = 5xto + 8xy - 6y3 - 4yto
T (x, y) = + x3y + ½ xto - 11xy - 6 årto
Umiddelbart er de manglende begrepene fullført, ifølge hvilke hvert polynom har:
R (x, y) = 0x3y + 5xto + 8xy - 6y3 - 4yto
T (x, y) = + x3y + ½ xto - 11xy + 0y3 - 6yto
Og dere er begge klare til å redusere like vilkår:
0x3y + 5xto + 8xy - 6y3 - 4yto
+ x3y + ½ xto - 11xy + 0y3 - 6yto +
-
+ x3og + 11 / 2xto - 3xy - 6y3 - 10 årto = R (x, y) + T (x, y)
Polynomiske tilleggsøvelser
- Øvelse 1
I den følgende summen av polynomer angir du begrepet som må gå tomt for å oppnå polynomsummen:
-5x4 + 0x3 + 2xto + 1
x5 + 2x4 - 21xto + 8x - 3
2x5 +9x3 -14x
-
-6x5+10x4 -0x3 + 5xto - 11x + 21
Løsning
For å få -6x5 det kreves et uttrykk for skjemaøksen5, slik at:
a + 1+ 2 = -6
Derfor:
a = -6-1-2 = -9
Og søkeordet er:
-9x5
-Fortsett på en lignende måte for å finne resten av vilkårene. Her er den for eksponent 4:
-5 + 2 + a = 10 → a = 10 + 5-2 = 13
Den manglende betegnelsen er: 13x4.
-For kreftene til x3 det er øyeblikkelig at begrepet må være -9x3, dermed er koeffisienten til det kubiske begrepet 0.
-Når det gjelder kvadratkrefter: a + 8 - 14 = -11 → a = -11 - 8 + 14 = -5 og begrepet er -5 xto.
-Den lineære termen er oppnådd ved hjelp av +8-14 = -11 → a = -11 + 14 - 8 = -5, den manglende termen er -5x.
-Til slutt er det uavhengige begrepet: 1 -3 + a = -21 → a = -19.
- Øvelse 2
Et flatt terreng er inngjerdet som vist på figuren. Finn et uttrykk for:
a) Omkretsen og
b) Dens område, i form av de angitte lengdene:
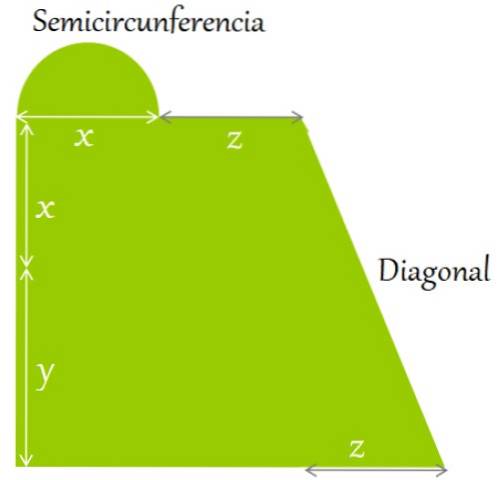
Løsning til
Omkretsen er definert som summen av sidene og konturene av figuren. Fra og med nederst til venstre, med urviseren, har vi:
Omkrets = y + x + halvcirkel lengde + z + diagonal lengde + z + z + x
Halvsirkelen har en diameter lik x. Siden radiusen er halvparten av diameteren, må vi:
Radius = x / 2.
Formelen for lengden på en komplett omkrets er:
L = 2π x Radius
Deretter:
Lengde på halvcirkel = ½. 2π (x / 2) = πx / 2
For sin del blir diagonalen beregnet med den pythagoreiske setningen som er brukt på sidene: (x + y) som er den vertikale siden og z, som er den horisontale:
Diagonal = [(x + y)to + zto]1/2
Disse uttrykkene er erstattet i en med omkretsen for å oppnå:
Omkrets = y + x + πx / 2 + z + [(x + y)to + zto]1/2+ z + x + z
Like vilkår reduseres, siden tillegget krever at resultatet forenkles så mye som mulig:
Omkrets = y + [x + π (x / 2) + x] + z + z + z + [(x + y)to + zto]1/2 = y + (2 + π / 2) x + 3z
Løsning b
Det resulterende området er summen av arealet til rektangelet, halvsirkelen og høyre trekant. Formlene for disse områdene er:
-Rektangel: base x høyde
-Halvsirkel: ½ π (Radius)to
-Triangel: base x høyde / 2
Rektangelområde
(x + y). (x + z) = xto + xz + yx + yz
Halvsirkelområde
½ π (x / 2)to = π xto / 8
Trekantområde
½ z (x + y) = ½ zx + ½ zy
Totalt areal
For å finne det totale arealet blir uttrykkene som er funnet for hvert delområde lagt til:
Totalt areal = xto + xz + yx + yz + (π xto / 8) + ½ zx + ½ zy
Og til slutt reduseres alle begrepene som er like:
Totalt areal = (1 + π / 8) xto + 3/2 xy + 3 / 2yz + yx
Referanser
- Baldor, A. 1991. Algebra. Redaksjonell Cultural Venezolana S.A.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Matematikk er gøy. Legge til og trekke fra polynomer. Gjenopprettet fra: mathsisfun.com.
- Monterey Institute. Legge til og trekke fra polynomer. Gjenopprettet fra: montereyinstitute.org.
- UC Berkeley. Algebra av polynomer. Gjenopprettet fra: math.berkeley.edu.



Ingen har kommentert denne artikkelen ennå.