De Bernoullis teorem, som beskriver oppførselen til en væske i bevegelse, ble bekjentgjort av matematikeren og fysikeren Daniel Bernoulli i sitt arbeid Hydrodynamikk. I følge prinsippet vil en ideell væske (uten friksjon eller viskositet) som sirkulerer gjennom en lukket ledning, ha en konstant energi i sin vei.
Teoremet kan utledes fra prinsippet om bevaring av energi og til og med fra Newtons andre bevegelseslov. I tillegg fastslår Bernoullis prinsipp også at en økning i hastigheten til en væske innebærer en reduksjon i trykket den utsettes for, en reduksjon i dens potensielle energi, eller begge deler samtidig..
Teoremet har mange forskjellige bruksområder, både i vitenskapens verden og i folks hverdag..
Konsekvensene er tilstede i flystyrken, i skorsteiner i hjem og industri, i vannrør, blant andre områder..
Artikkelindeks
Selv om Bernoulli var den som utledet at trykket synker når strømningshastigheten øker, er sannheten at det var Leonhard Euler som faktisk utviklet Bernoulli-ligningen i den formen den er kjent i dag..
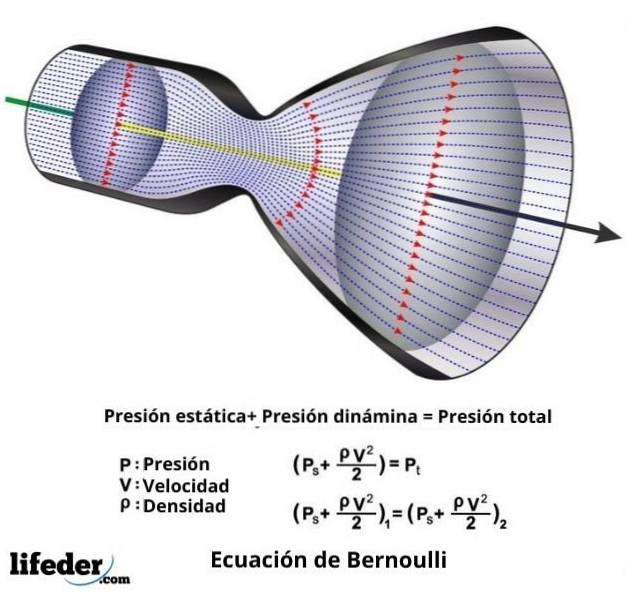
I alle fall er ligningen til Bernoulli, som ikke er noe annet enn det matematiske uttrykket for hans teorem, følgende:
vto ∙ ƿ / 2 + P + ƿ ∙ g ∙ z = konstant
I dette uttrykket er v væskens hastighet gjennom seksjonen som er vurdert, ƿ er væskens tetthet, P er væsketrykket, g er verdien av tyngdekraftsakselerasjonen, og z er høyden målt i retning av tyngdekraften.
Det er implisitt i Bernoullis ligning at energien til en væske består av tre komponenter:
- En kinetisk komponent, som er den som kommer fra hastigheten med hvilken væske beveger seg.
- En potensiell eller gravitasjonskomponent, som skyldes høyden der væsken er.
- En trykkenergi, som er den som væsken har som en konsekvens av trykket den utsettes for.
På den annen side kan Bernoullis ligning også uttrykkes slik:
v1 to ∙ ƿ / 2 + P1 + ƿ ∙ g ∙ z1 = vtoto ∙ ƿ / 2 + Pto + ƿ ∙ g ∙ zto
Dette siste uttrykket er veldig praktisk for å analysere endringene som en væske opplever når noen av elementene som utgjør ligningen endres.
Ved visse anledninger er endringen i ρgz-begrepet i Bernoullis ligning minimal sammenlignet med den som de andre begrepene opplever, så den kan neglisjeres. For eksempel skjer dette i strømmer som et fly opplever under flyturen..
Ved disse anledninger uttrykkes Bernoullis ligning som følger:
P + q = P0
I dette uttrykket er q dynamisk trykk og tilsvarer v to ∙ ƿ / 2, og P0 er det som kalles totaltrykk og er summen av det statiske trykket P og det dynamiske trykket q.
Bernoullis teorem har mange og mangfoldige anvendelser innen så mangfoldige felt som vitenskap, ingeniørfag, sport, etc..
En interessant applikasjon finnes i utformingen av peiser. Skorstene er bygget høyt for å oppnå større trykkforskjell mellom bunnen og skorsteinens utløp, takket være det er lettere å trekke ut forbrenningsgassene.
Bernoullis ligning gjelder selvfølgelig også studiet av bevegelse av væskestrømmer i rør. Fra ligningen følger det at en reduksjon i rørets tverrsnittsareal, for å øke hastigheten til væsken som passerer gjennom det, også innebærer en reduksjon i trykket.
Bernoulli-ligningen brukes også i luftfart og i kjøretøyer i Formel 1. Når det gjelder luftfart, er Bernoulli-effekten opphavet til heisen av fly.
Flyvinger er designet med det mål å oppnå større luftstrøm øverst på vingen.
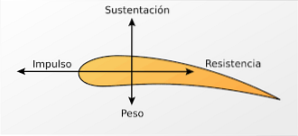
Dermed er lufthastigheten i den øvre delen av vingen høy, og derfor er trykket lavere. Denne trykkforskjellen produserer en vertikalt oppadrettet kraft (løftekraft) som gjør at flyet kan sveve i luften. En lignende effekt er oppnådd i rulleskinnene til Formel 1-biler.
Gjennom et rør med et tverrsnitt på 4,2 cmto det strømmer en vannstrøm ved 5,18 m / s. Vannet kommer ned fra en høyde på 9,66 m til et lavere nivå med en høyde på null, mens tverrsnittsarealet på røret øker til 7,6 cmto.
a) Beregn hastigheten på vannstrømmen på lavere nivå.
b) Bestem trykket på det nedre nivået, vel vitende om at trykket på det øvre nivået er 152000 Pa.
a) Gitt at strømmen må bevares, er det sant at:
SpørsmålØvre nivå = Qlavere nivå
v1 . S1 = vto . Sto
5,18 m / s. 4,2 cmto = vto . 7,6 cm ^to
Løsning for oppnås at:
vto = 2,86 m / s
b) Bruke Bernoullis teorem mellom de to nivåene, og ta i betraktning at tettheten av vann er 1000 kg / m3 , det oppnås at:
v1 to ∙ ƿ / 2 + P1 + ƿ ∙ g ∙ z1 = vtoto ∙ ƿ / 2 + Pto + ƿ ∙ g ∙ zto
(1/2). 1000 kg / m3 . (5,18 m / s)to + 152000 + 1000 kg / m3 . 10 m / sto . 9,66 m =
= (1/2). 1000 kg / m3 . (2,86 m / s)to + Pto + 1000 kg / m3 . 10 m / sto . 0 m
Løsning for Pto du kommer til:
Pto = 257926,4 Pa
Ingen har kommentert denne artikkelen ennå.