
Superposition teorem forklaring, applikasjoner, løste øvelser
De setning om superposisjon, I elektriske kretser fastslår det at spenningen mellom to punkter, eller strømmen gjennom dem, er den algebraiske summen av spenningene (eller strømmen hvis det er tilfelle), på grunn av hver kilde, som om hver og en handlet på en annen måte Uavhengig.
Denne teoremet lar oss analysere lineære kretser som inneholder mer enn en uavhengig kilde, siden det bare er nødvendig å beregne bidraget til hver enkelt separat..

Lineær avhengighet er avgjørende for at teoremet skal gjelde. En lineær krets er en hvis respons er direkte proporsjonal med inngangen.
For eksempel sier Ohms lov som gjelder en elektrisk motstand at V = i.R, hvor V er spenningen, R er motstanden e Jeg er gjeldende. Det er da en lineær avhengighet av spenning og strøm i en motstand.
I lineære kretser brukes superposisjonsprinsippet under hensyntagen til følgende:
-Hver uavhengige spenningskilde må vurderes separat, og for dette er det nødvendig å slå av alle de andre. Det er nok å sette til 0 V alle de som ikke er under analyse, eller å erstatte dem i skjemaet med kortslutning.
-Hvis kilden er aktuell, må du åpne kretsen.
-Når vi vurderer den interne motstanden til både strøm- og spenningskilder, må de forbli på plass og utgjøre en del av resten av kretsen..
-Hvis det er avhengige kilder, må de forbli slik de vises i kretsen.
Artikkelindeks
- 1 Søknader
- 2 trinn for å anvende superposisjonssetningen
- 3 Løst øvelser
- 3.1 - Eksempel 1
- 3.2 - Øvelse 2
- 4 Referanser
applikasjoner
Superposisjonssetningen brukes til å oppnå enklere og lettere å håndtere kretser. Men det bør alltid huskes at det bare gjelder de med lineære responser, som sagt i begynnelsen.
Så det kan for eksempel ikke brukes direkte til å beregne effekt, siden kraft er relatert til strøm av:
P = ito R
Siden strømmen er kvadrat, er ikke responsen lineær. Det er heller ikke aktuelt for magnetiske kretser som involverer transformatorer..
På den annen side gir superposisjonssatsen muligheten til å vite hvilken effekt hver kilde har på kretsen. Og selvfølgelig er det gjennom applikasjonen mulig å løse det fullstendig, det vil si å kjenne strøm og spenning gjennom hver motstand.
Superposisjonssetningen kan også brukes sammen med andre kretssetninger, for eksempel Thévenins, for å løse mer komplekse konfigurasjoner..
I vekselstrømkretser er setningen også nyttig. I dette tilfellet jobber vi med impedanser i stedet for motstander, så lenge den totale responsen til hver frekvens kan beregnes uavhengig..
Til slutt gjelder teoremet i elektroniske systemer både for likestrøm og vekselstrømsanalyse, separat.
Fremgangsmåte for å anvende superposisjonssatsen
-Deaktiver alle uavhengige kilder ved å følge instruksjonene i begynnelsen, bortsett fra den som skal analyseres.
-Bestem utgangen, enten spenning eller strøm, som den enkelte kilden produserer.
-Gjenta de to trinnene som er beskrevet for alle andre kilder.
-Beregn den algebraiske summen av alle bidragene som ble funnet i de foregående trinnene.
Løst øvelser
De utførte eksemplene nedenfor klargjør bruken av teoremet i noen enkle kretsløp.
- Eksempel 1
I kretsen vist i følgende figur, finn strømmen gjennom hver motstand ved hjelp av superposisjonssatsen.
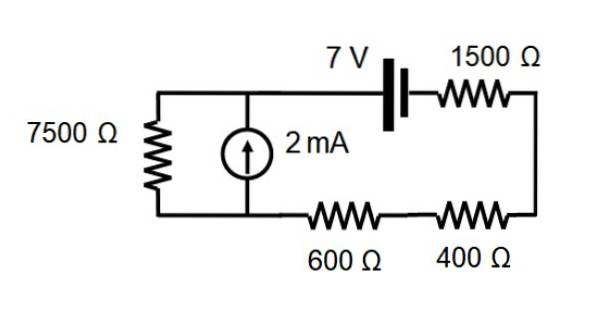
Løsning
Spenningskildebidrag
Til å begynne med er den aktuelle kilden eliminert, noe som får kretsen til å se slik ut:

Den ekvivalente motstanden blir funnet ved å legge til verdien av hver motstand, siden de alle er i serie:
7500 +600 +400 + 1500 Ω = 10.000 Ω
Bruk av Ohms lov V = I.R og tømme strømmen:
I = V / R = 7 / 10.000 A = 0.0007 A = 0,7 mA
Denne strømmen er den samme for alle motstander.
Bidrag fra den nåværende kilden
Spenningskilden elimineres umiddelbart, for å kun fungere med strømkilden. Den resulterende kretsen er vist nedenfor:
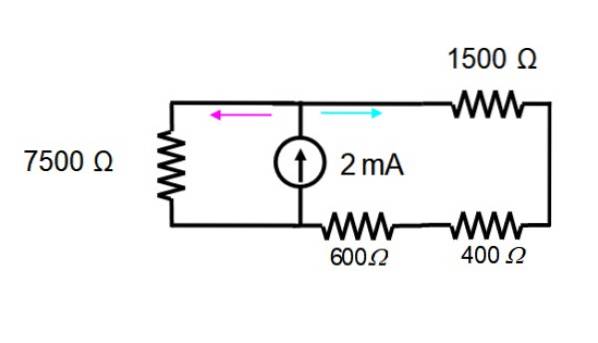
Motstandene på skjermen til høyre er i serie og kan erstattes av en enkelt:
600 +400 + 1500 Ω = 2500 Ω
Den resulterende kretsen ser slik ut:
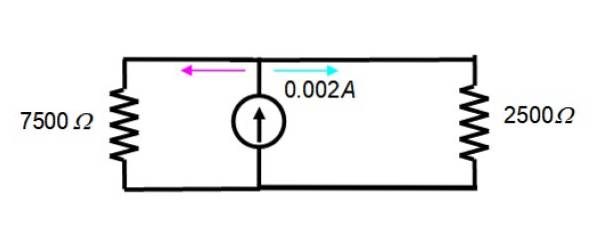
Strømmen på 2 mA = 0,002 A er delt mellom de to motstandene i figuren, derfor er ligningen til strømdeleren gyldig:
Jegx = (Rekv/ Rx) JEGT
Hvor Jegx er strømmen i motstanden Rx, Rekv symboliserer tilsvarende motstand e JegT er totalstrømmen. Det er nødvendig å finne tilsvarende motstand mellom begge, vel vitende om at:
1 / Rekv = (1 / R.1) + (1 / Rto)
Derfor:
1 / Rekv = (1/7500) + (1/2500) = 1/1875 → Rekv = 1875 Ω
For denne andre kretsen blir strømmen gjennom 7500 Ω motstanden funnet ved å erstatte verdier i den nåværende skillelinjen:
Jeg7500 Ω = (1875/7500). 0,002 A = 0,0005 A = 0,5 mA
Mens den som passerer gjennom 2500 Ω motstanden er:
Jeg2500 Ω = 2 mA - 0,5 mA = 1,5 mA
Anvendelse av superposisjonssatsen
Nå brukes superposisjonssatsen for hver motstand, og starter med 400 Ω:
Jeg400 Ω = 1,5 mA - 0,7 mA = 0,8 mA
Viktig: for denne motstanden, strømmen blir trukket, når de sirkulerer i motsatt retning, i henhold til en nøye observasjon av figurene, der strømningsretningene har forskjellige farger.
Den samme strømmen går likt gjennom 1500 Ω og 600 Ω motstandene, siden de alle er i serie.
Teoremet blir deretter brukt for å finne strømmen gjennom 7500 Ω motstanden:
Jeg7500 Ω = 0,7 mA + 0,5 mA = 1,2 mA
Viktig: i tilfelle 7500 Ω motstand, merk deg at strømmen legger opp, fordi i begge kretsløp sirkulerer de i samme retning når de går gjennom denne motstanden. Igjen er det nødvendig å nøye observere retningene i strømmen.
- Øvelse 2
Finne strøm og spenning over 12 Ω motstanden ved hjelp av superposisjonssatsen.
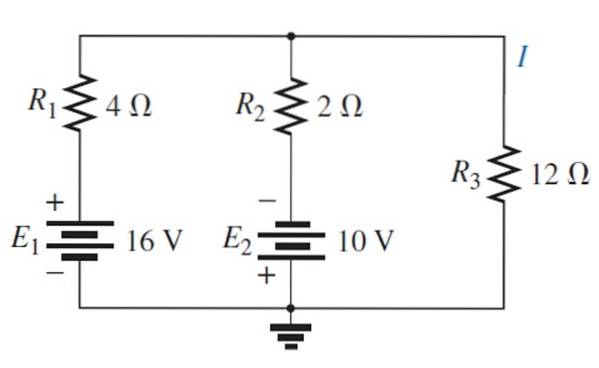
Løsning
Skrift E erstattes1 med kortslutning:
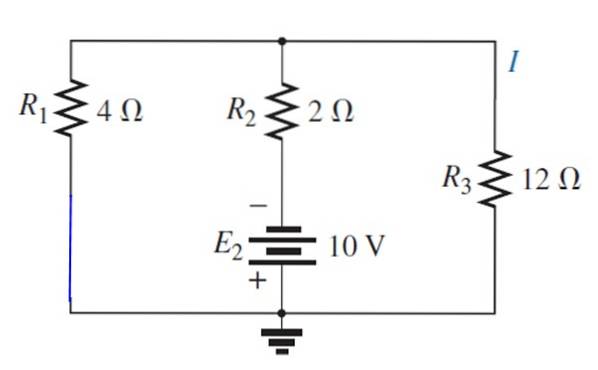
Den resulterende kretsen tegnes som følger for å enkelt visualisere motstandene som forblir parallelle:
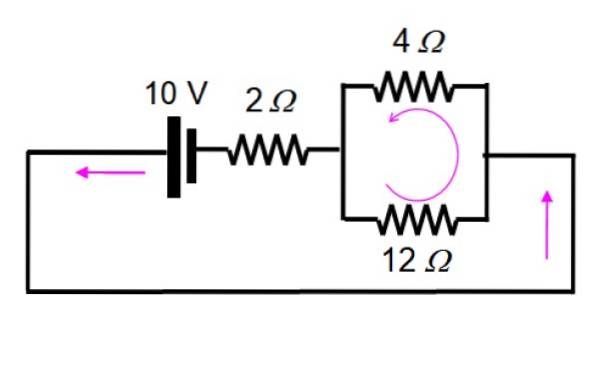
Og nå løses det ved å bruke serier og parallelle:
1 / Rekv = (1/12) + (1/4) = 1/3 → Rekv = 3 Ω
Denne motstanden er igjen i serie med den 2 Ω, derfor er den totale motstanden 5 Ω. Den totale strømmen er:
I = V / R = 10 V / 5 Ω = 2 A.
Denne strømmen er delt inn som:
Jeg12Ω = (3/12) 2 A = 0,5 A.
Derfor er spenningen:
V12Ω = 0,5 A × 12 Ω = 6 V
Nå er kilde E aktivert1:
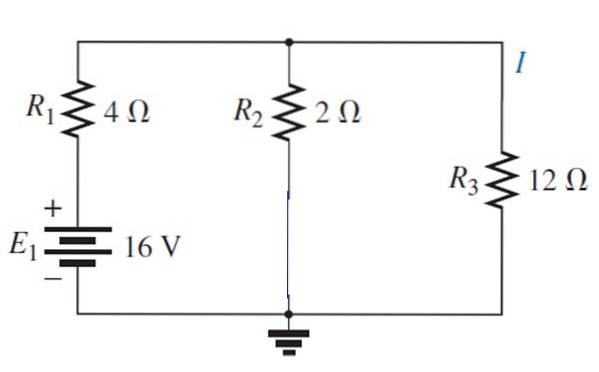
Den resulterende kretsen kan tegnes slik:

1 / Rekv = (1/12) + (1/2) = 7/12 → Rekv = 12/7 Ω
Og i serie med den av 4 Ω tilsvarende motstandsresultater 40/7 Ω. I dette tilfellet er den totale strømmen:
I = V / R = 16 V / (40/7) Ω = 14/5 A.
Spenningsdeleren påføres igjen med disse verdiene:
Jeg12Ω = ((12/7) / 12) (14/5) A = 0,4 A.
Den resulterende strømmen er: 0,5 - 0,4 A = 0,1 A.. Vær oppmerksom på at de har blitt trukket, siden strømmen fra hver kilde har en annen følelse, slik man kan se i den opprinnelige kretsen.
Spenningen over motstanden er:
V12Ω = 0,4 A × 12 Ω = 4,8 V
Til slutt er den totale spenningen: 6V-4,8V = 1,2V
Referanser
- Alexander, C. 2006. Grunnleggende om elektriske kretser. 3.. Utgave. Mc Graw Hill.
- Boylestad, R. 2011. Introduksjon til kretsanalyse. 2. plass. Utgave. Pearson.
- Dorf, R. 2006. Introduksjon til elektriske kretser. 7. Utgave. John Wiley & Sons.
- Edminister, J. 1996. Elektriske kretser. Schaum-serien. 3.. Utgave. Mc Graw Hill
- Wikipedia. Nåværende skillelinje. Gjenopprettet fra: es.wikipedia.org.



Ingen har kommentert denne artikkelen ennå.