
Thévenins setning hva den består av, applikasjoner og eksempler
De Thévenins setning sier at en krets med terminalene A og B kan erstattes av en ekvivalent en som består av en kilde og en seriemotstand, hvis verdier gir samme potensialforskjell mellom A og B og samme impedans som den opprinnelige kretsen.
Denne teoremet ble kjent i 1883 av den franske ingeniøren Léon Charles Thévenin, men det hevdes at den ble bekjentgjort tretti år tidligere av den tyske fysikeren Hermann von Helmholtz.

Dens nytte ligger i det faktum at den enkle Thévenin-ekvivalente kretsen oppfører seg på samme måte som originalen, selv når den opprinnelige kretsen er kompleks eller ukjent, for formål eller belastning som er plassert mellom terminalene A og B.
Artikkelindeks
- 1 Hvordan beregner du ekvivalent spenning trinn for trinn?
- 1.1 - Eksperimentelt
- 1.2 - Løsning av kretsen
- 2 Anvendelser av Thévenins teorem (del I)
- 2.1 Eksempel 1a (beregning av ekvivalent spenning trinn for trinn)
- 2.2 Eksempel 1b (strøm i lasten ved bruk av Thévenin-ekvivalenten)
- 3 Bevis på Thévenins teorem
- 4 Anvendelse av Thévenins teorem (del II)
- 4.1 Eksempel 2a (ekvivalent motstand mot Thévenin)
- 4.2 Eksempel 2b
- 4.3 Eksempel 2c
- 5 Anvendelse av Thévenins teorem (del III)
- 5.1 Eksempel 3
- 6 Referanser
Hvordan beregner du ekvivalent spenning trinn for trinn?
Spenningen eller potensialforskjellen til ekvivalent krets kan oppnås på følgende måter:
- Eksperimentelt
Å skaffe ekvivalent Thévenin-spenning
Hvis det er en enhet eller et utstyr som er i en “svart boks”, måles potensialforskjellen mellom terminalene A og B med et voltmeter eller et oscilloskop. Det er veldig viktig at ingen belastning eller impedans plasseres mellom terminalene A og B.
Et voltmeter eller et oscilloskop representerer ingen belastning på terminalene, siden begge enhetene har en veldig stor impedans (ideelt sett uendelig) og det ville være som om terminalene A og B var uten belastning. Spenningen eller spenningen oppnådd på denne måten er den tilsvarende Thévenin-spenningen.
Å få Thévenin tilsvarende impedans
For å oppnå ekvivalent impedans fra en eksperimentell måling, plasseres en kjent motstand mellom terminalene A og B og spenningsfallet eller spenningssignalet måles med et oscilloskop..
Fra spenningsfallet i den kjente motstanden mellom terminalene, kan strømmen som strømmer gjennom den oppnås.
Produktet av strømmen oppnådd med den ekvivalente motstanden pluss spenningsfallet målt i den kjente motstanden er lik den tidligere oppnådde Thévenin-spenningen. Fra denne likheten blir den tilsvarende Thévenin-impedansen fjernet.
- Løse kretsen
Beregning av Thévenin ekvivalent spenning
For det første kobles enhver belastning eller impedans fra terminalene A og B.
Som kretsen er kjent, brukes meshteori eller Kirchhoffs lover for å finne spenningen ved terminalene. Denne spenningen vil være ekvivalent med Thévenin.
Beregning av Thévenin ekvivalent impedans
For å oppnå tilsvarende impedans går vi videre til:
- Erstatt spenningskildene til den opprinnelige kretsen med kortslutning "nullimpedans" og strømkildene til den originale kretsen med åpne "uendelig impedans".
- Deretter beregnes ekvivalent impedans i henhold til reglene for serieimpedanser og parallelle impedanser.
Anvendelser av Thévenins teorem (del I)
Vi vil bruke Thévenins teorem for å løse noen kretsløp. I denne første delen vurderer vi en krets som bare har spenningskilder og motstand.
Eksempel 1a (beregning av ekvivalent stress trinnvis)
Figur 2 viser kretsen som er i en himmelboks som har henholdsvis to elektromotoriske kraftbatterier V1 og V2 og motstandene R1 og R2, kretsen har terminaler A og B der en belastning kan kobles til.
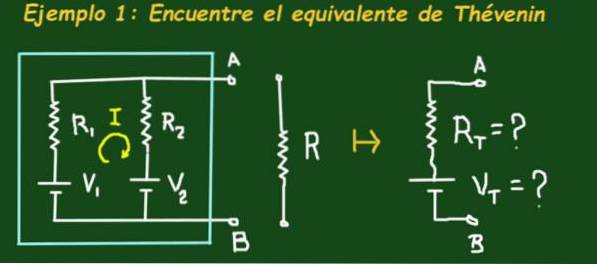
Målet er å finne Thévenin-ekvivalent krets, det vil si å bestemme Vt- og Rt-verdiene til den tilsvarende kretsen. Bruk følgende verdier: V1 = 4V, V2 = 1V, R1 = 3Ω, R2 = 6Ω, og R = 1Ω.
Trinnvis løsning
Trinn 1
Vi vil bestemme spenningen på terminalene A og B når ingen belastning legges på dem.
Steg 2
Kretsen som skal løses består av et enkelt maske gjennom hvilket en strøm I sirkulerer som vi har tatt positivt med urviseren.
Trinn 3
Vi går gjennom masken og begynner med det nedre venstre hjørnet. Stien fører til følgende ligning:
V1 - I * R1 - I * R2 - V2 = 0
Trinn 4
Vi løser for nettstrømmen I og får:
I = (V1 -V2) / (R1 + R2) = (4V - 1V) / (3Ω + 6Ω) = ⅓ A
Trinn 5
Med nettstrømmen kan vi bestemme spenningsforskjellen mellom A og B, som er:
Vab = V1 - I * R1 = 4V - ⅓ A * 3Ω = 3V
Det vil si at Thevenin-ekvivalent spenning er: Vt = 3V.
Trinn 6 (Thévenin ekvivalent motstand)
Vi fortsetter nå med å beregne Thévenin-ekvivalent motstand, for hvilken og som tidligere nevnt, blir spenningskildene erstattet av en kabel.
I så fall har vi bare to motstander parallelt, så Thévenin-ekvivalente motstand er:
Rt = (R1 * R2) / (R1 + R2) = (3Ω * 6Ω) / (3Ω + 6Ω) = 2Ω
Eksempel 1b (strøm i lasten ved bruk av Thévenin-ekvivalenten)
Koble som en belastning til terminalene A og B, en motstand R = 1Ω til ekvivalent krets og finn strømmen som strømmer gjennom belastningen.
Løsning
Når motstanden R er koblet til Thevenin-ekvivalent krets, har vi en enkel krets som består av en kilde Vt en motstand Rt i serie med motstanden R.
Vi vil kalle Ic strømmen som strømmer gjennom lasten R, slik at maske ligningen ser slik ut:
Vt - Ic * Rt - Ic * R = 0
hvorfra det følger at Ic er gitt av:
Ic = Vt / (Rt + R) = 3V / (2Ω + 1Ω) = 1 A.
Bevis på Thévenins teorem
For å verifisere at Thévenins teorem holder, koble R til den opprinnelige kretsen og finn strømmen som strømmer gjennom R ved å bruke maskeloven på den resulterende kretsen.
Den resulterende kretsen forblir og maskelinjene forblir som vist i følgende figur:
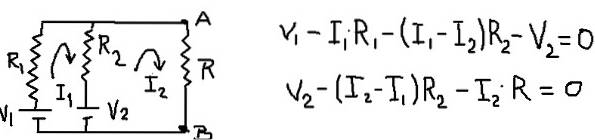
Ved å legge til nettinglikningene er det mulig å finne nettstrømmen I1 som en funksjon av den nåværende I2. Deretter blir den erstattet i den andre maske ligningen, og en ligning er igjen med I2 som den eneste ukjente. Tabellen nedenfor viser operasjonene.
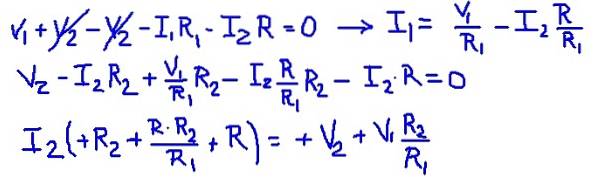
Deretter erstattes verdiene til motstanden og spenningen til kildene, og oppnår den numeriske verdien til nettstrømmen I2.

Maskestrømmen I2 er strømmen som strømmer gjennom lastmotstanden R, og verdien funnet av 1 A faller helt sammen med den som tidligere ble funnet med den tilsvarende Thévenin-kretsen..
Anvendelse av Thévenins teorem (del II)
I denne andre delen vil Thévenin-teoremet brukes i en krets som har spenningskilder, strømkilde og motstand.
Eksempel 2a (Thévenin ekvivalent motstand)
Målet er å bestemme Thévenin-ekvivalent krets som tilsvarer kretsen i følgende figur, når terminalene er uten motstand på 1 ohm, blir motstanden plassert og strømmen som sirkulerer gjennom den bestemmes.
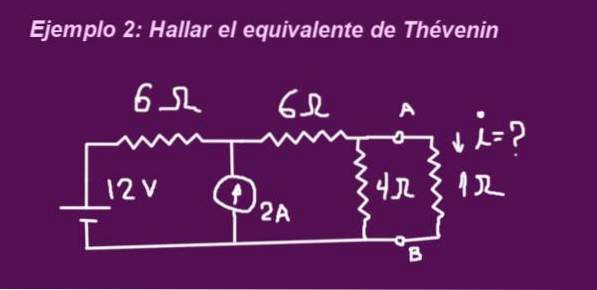
Løsning
For å finne tilsvarende motstand, fjern lastmotstanden (i dette tilfellet 1 ohm). Spenningskilder erstattes også av kortslutning og strømkilder av åpen krets..
På denne måten er kretsen som tilsvarer motstanden beregnet for den som er vist nedenfor:
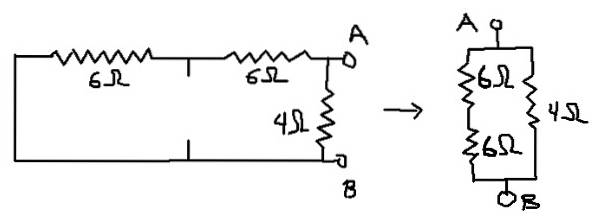
Rab = (12Ω * 4Ω) / (12Ω + 4Ω) = 3Ω som er Thevenin-ekvivalent motstand (Rth).
Eksempel 2b
Beregn Thévenin ekvivalent spenning.
Løsning
For å beregne Thévenin-ekvivalent spenning vurderer vi følgende krets, der vi vil plassere strømene i I1 og I2 i grenene som er angitt i følgende figur:
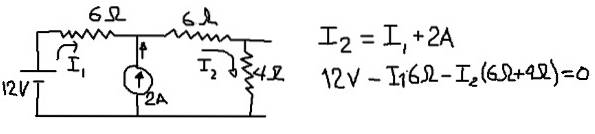
Den forrige figuren viser ligningen til strømnodene og ligningen av spenninger når det eksterne nettet krysses. Fra den andre av ligningene blir nåværende I1 ryddet:
I1 = 2 - I2 * (5/3)
Denne ligningen er substituert i ligningen til nodene:
I2 = 2 - (5/3) I2 + 2 ===> I2 (8/3) = 4 ===> I2 = 12/8 = 1,5 A
Dette betyr at spenningsfallet over 4 ohm-motstanden er 6 volt..
Kort sagt er Théveninspenningen Vth = 6 V..
Eksempel 2c
Finne Thevenin-ekvivalent krets og strøm i lastmotstanden.
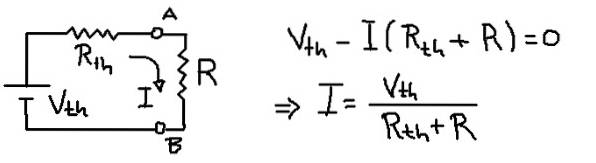
Løsning
Den forrige figuren viser Thévenin-ekvivalente kretsen med lastmotstanden R. Fra spenningsligningen i masken trekkes strømmen I som strømmer gjennom lastmotstanden R.
I = Vth / (Rth + R) = 6V / (3Ω + 1Ω) = 1,5 A
Anvendelse av Thévenins teorem (del III)
I denne tredje delen av anvendelsen av Thévenins setning vurderes en vekselstrømskrets som inneholder en vekselstrømskilde, en kondensator, en induktans og en motstand..
Eksempel 3
Målet er å finne Thévenin Circuit tilsvarende følgende krets:
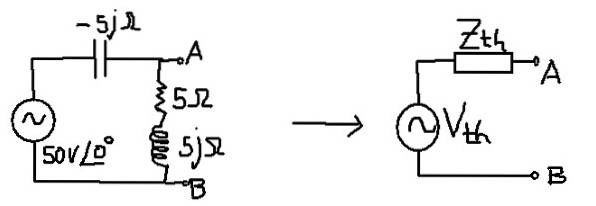
Løsning
Den ekvivalente impedansen tilsvarer kondensatorens parallell med seriekombinasjonen av motstand og induktans.
Det omvendte av den tilsvarende impedansen er gitt av:
Zeq ^ -1 = (-5j) ^ - 1 + (5 + 5j) ^ - 1 = (1/5) j + ((1/10 + (1/10) j) = (1/10 + 3 / 10 j) Mho
Og den tilsvarende impedansen vil da være:
Zeq = (1-3 j) Ohm
Den komplekse strømmen I kan avledes fra maske ligningen:
50V∠0 - I (-5 j + 5 + 5j) = 50V∠0 - I * 5 = 0 ===> I = 10A ∠0
Nå beregnes spenningsfallet i motstanden pluss induktansen, det vil si spenningen Vab som vil være ekvivalent Théveninspenning:
Vab = I * (5 + 5 j) Ω = 10A ∠0 * 5Ω∠45º = 50V∠45º
Med andre ord, ekvivalent spenning har samme toppverdi som den opprinnelige kilden, men er 45 grader utenfor fase: Vth = 50V∠45º
Referanser
- Elektronikkopplæring, Thevenins teorem. Gjenopprettet fra: electronics-tutorials.ws
- Nettverksteori spørsmål og svar. Thevenins teorem. Gjenopprettet fra: sanfoundry.com
- Thevenins teorem. Trinnvis fremgangsmåte. Gjenopprettet fra: electrictechnology.org
- Thevenins teorem. Løst eksempel trinn for trinn. Gjenopprettet fra: electricsimple.blogspot.com
- Workshop om Thevenins og Nortons teoremer. Gjenopprettet fra: web.iit.edu
- Wikipedia. Thévenins teorem. Gjenopprettet fra: wikipedia.com


Ingen har kommentert denne artikkelen ennå.