Torricellis teorem hva den består av, formler og øvelser

De Torricellis teorem Torricelli-prinsippet sier at hastigheten på væsken som kommer ut gjennom hullet i veggen til en tank eller container er identisk med hastigheten til en gjenstand som får falle fritt fra en høyde som er lik den av den frie overflaten av væsken opp til hullet.

Teoremet er illustrert i følgende figur:

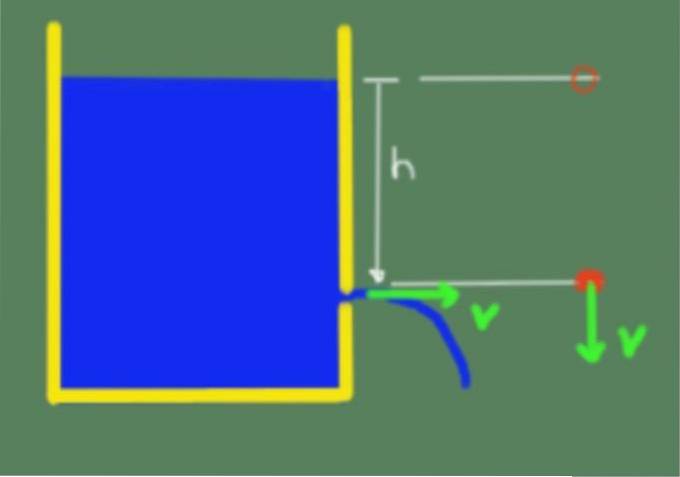
På grunn av Torricellis teorem kan vi deretter bekrefte at væskens utgangshastighet gjennom en åpning som er i høyden h under den frie overflaten av væsken, er gitt med følgende formel:

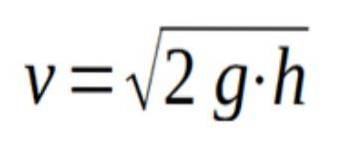
Hvor g er tyngdeakselerasjonen og h er høyden fra hullet til den frie overflaten av væsken.

Evangelista Torricelli var en fysiker og matematiker født i byen Faenza, Italia i 1608. Torricelli er kreditert oppfinnelsen av kvikksølvbarometeret og i anerkjennelse er det en trykkenhet kalt “torr”, tilsvarende en millimeter kvikksølv (mm Hg).

Artikkelindeks

• 1 Bevis for teoremet
  • 1.1 Fallende gjenstand
  • 1.2 Væske som kommer ut av hullet
• 2 Løst øvelser
  • 2.1 Øvelse 1
• 3 I) Det lille utløpsrøret til en vanntank er 3 m under vannoverflaten. Beregn utløpshastigheten til vannet.
  • 3.1 Øvelse 2
  • 3.2 Øvelse 3
• 4 Referanser

Bevis på teoremet

I Torricellis teorem og i formelen som gir hastigheten, antar det at viskositetstapene er ubetydelige, akkurat som i fritt fall antas det at friksjonen på grunn av luften rundt den fallende gjenstanden er ubetydelig..

Ovennevnte antagelse er i de fleste tilfeller rimelig og innebærer også bevaring av mekanisk energi.

For å bevise setningen vil vi først finne formelen for hastigheten til et objekt som frigjøres med null starthastighet, fra samme høyde som væskeoverflaten i tanken..

Prinsippet om bevaring av energi vil bli brukt for å oppnå hastigheten på den fallende gjenstanden akkurat når den har kommet ned i høyden h lik det fra hull til fri overflate.

Siden det ikke er friksjonstap, er det gyldig å anvende prinsippet om bevaring av mekanisk energi. Anta at den fallende gjenstanden har masse m og høyden h måles fra utløpsnivået til væsken.

Fallende gjenstand

Når objektet frigjøres fra en høyde som er lik den av den frie overflaten av væsken, er dens energi bare gravitasjonspotensial, siden hastigheten er null og derfor er den kinetiske energien null. Den potensielle energien Ep er gitt av:

Ep = m g h

Når den passerer foran hullet, er høyden null, så er den potensielle energien null, så den har bare kinetisk energi Ec gitt av:

Ec = ½ m v^to

Siden energien er bevart Ep = Ec fra det som oppnås:

½ m v^to = m g h

Løser for fart v Torricelli-formelen oppnås deretter:

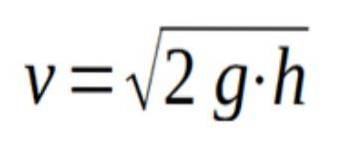
Væske kommer ut av hullet

Deretter finner vi væskens utgangshastighet gjennom hullet for å vise at den sammenfaller med det som nettopp ble beregnet for et fritt fallende objekt.

For dette vil vi basere oss på Bernoullis prinsipp, som ikke er noe annet enn bevaring av energi brukt på væsker.

Bernoullis prinsipp er formulert slik:

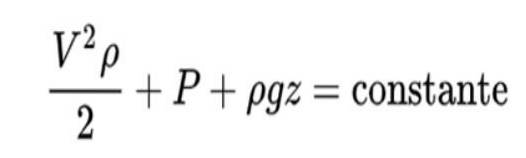
Tolkningen av denne formelen er som følger:

• Den første termen representerer væskeens kinetiske energi per volumsenhet
• Den andre representerer arbeidet utført ved trykk per tverrsnittsenhet.
• Den tredje representerer gravitasjonspotensialenergien per væskeenhet..

Når vi tar utgangspunkt i at det er en ideell væske, i ikke-turbulente forhold med relativt lave hastigheter, er det relevant å bekrefte at den mekaniske energien per volumenhet i væsken er konstant i alle regioner eller tverrsnitt av samme..

I denne formelen V er væskens hastighet, ρ væskens tetthet, P trykk og z vertikal posisjon.

Figuren nedenfor viser Torricelli-formelen med utgangspunkt i Bernoullis prinsipp.

Vi bruker Bernoullis formel på den frie overflaten av væsken betegnet med (1) og på utgangshullet betegnet med (2). Nullhodet er valgt i flukt med utløpshullet.

Under forutsetningen om at tverrsnittet i (1) er mye større enn i (2), kan vi da anta at hastigheten for nedstigning av væsken i (1) er praktisk talt ubetydelig.

Dette er grunnen til at V₁= 0, trykket som væsken utsettes for i (1) er atmosfærisk trykk og høyden målt fra åpningen er h.

For utløpsdelen (2) antar vi at utløpshastigheten er v, trykket som væsken utsettes for ved utløpet er også atmosfærisk trykk og utløpshøyden er null.

Verdiene som tilsvarer seksjonene (1) og (2) er erstattet i Bernoullis formel og sett like. Likheten holder fordi vi antar at væsken er ideell og at det ikke er viskøse friksjonstap. Når alle vilkårene er forenklet, oppnås hastigheten ved utgangshullet.

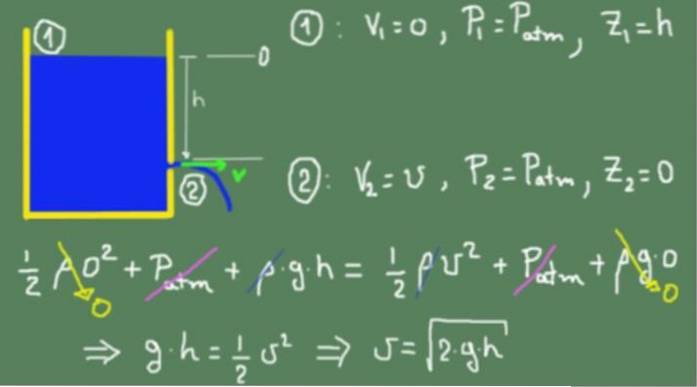
Ruten ovenfor viser at resultatet er det samme som for et fritt fallende objekt,

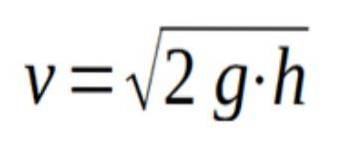
Løst øvelser

Øvelse 1

Jeg) Det lille utløpsrøret til en vanntank er 3 m under vannoverflaten. Beregn utløpshastigheten til vannet.

Løsning:

Følgende figur viser hvordan Torricellis formel blir brukt i denne saken.

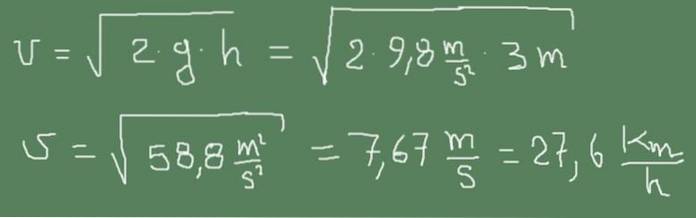
Øvelse 2

II) Forutsatt at utløpsrøret til tanken fra forrige øvelse har en diameter på 1 cm, beregne vannutløpsstrømmen.

Løsning:

Strømningshastigheten er volumet av væske som går ut per tidsenhet, og beregnes ganske enkelt ved å multiplisere området til utgangsåpningen med utgangshastigheten.

Følgende figur viser detaljene i beregningen.

Øvelse 3

III) Bestem hvor høy den frie overflaten av vannet er i en beholder hvis du vet

at i et hull i bunnen av beholderen kommer vannet ut ved 10 m / s.

Løsning:

Selv når hullet er i bunnen av beholderen, kan Torricelli-formelen fortsatt brukes.

Følgende figur viser detaljene i beregningene.

Referanser

1. Wikipedia. Torricellis teorem.
2. Hewitt, P. Konseptuell fysikk. Femte utgave.119.
3. Young, Hugh. 2016. Sears-Zemanskys universitetsfysikk med moderne fysikk. 14. utg. Pearson. 384.