
Forklaringsfaktorsetning, eksempler, øvelser
De faktorsetning sier at et polynom P (x) er delbart med et binomium av formen (x - a) hvis x = a er en rot av P (x), det vil si P (a) = 0. Det sies at et polynom kan deles mellom en annen når dens rest eller resten er null.
Et polynom er et uttrykk for formen:
P (x) = an xn + tiln-1 xn-1 +… + A1 x + a0

Hvor:
-n er graden av polynomet, der n er det største heltallet som den uavhengige variabelen x heves til,
-Verdiene tiln, tiln-1 ,… + A1 , til0 er koeffisientene til polynomet, som vanligvis er reelle tall, men kan også være komplekse tall.
Et polynom av grad n kan spaltes som produktet av n binomaler av formen:
(x - rJeg)
Hvor rJeg er den første roten til P (x):
P (x) = an (x - r1) (x - rto) ... (X - rn)
Siden antallet røtter til et polynom er lik graden.
Artikkelindeks
- 1 Eksempler
- 1.1 - Eksempel 1
- 1.2 - Eksempel 2
- 2 Øvelser
- 2.1 - Øvelse 1
- 2.2 - Øvelse 2
- 3 Referanser
Eksempler
- Eksempel 1
La oss i tilfelle vurdere polynomet:
P (x) = 3⋅xto - 7⋅x + 2
Du vil vite om dette polynomet kan deles med binomialet (x - 2). Hvis faktorsetningen brukes, må vi evaluere P (x = 2) for å vite om verdien 2 er en rot eller ikke. Vi fortsetter deretter med å evaluere uttrykket:
P (2) = 3⋅22 - 7⋅2 + 2 = 3⋅4 - 7⋅2 + 2 = 12 - 14 + 2 = 12 - 12 = 0.
Det viser seg at x = 2 er roten til P (x), så i følge faktorsetningen er binomialet (x - 2) effektivt en faktor på P (x).
La oss gå videre til direkte bekreftelse ved å dele. Detaljene om hvordan delingen utføres er vist i følgende figur:
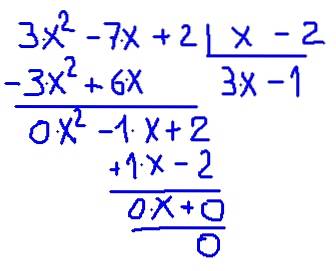
Det er bekreftet at kvotienten mellom P (x) og (x-2) gir et polynom av lavere grad kalt kvotienten C (x) = 3⋅x - 1 med resten 0.
Vi kan oppsummere resultatet som følger:
(3⋅xto - 7⋅x + 2) ÷ (x -2) = (3⋅x - 1) + 0
Det forrige uttrykket kan skrives på en annen måte, bare husk at utbyttet P (x) er lik produktet av deleren (x -2) med kvotienten (3⋅x - 1) pluss resten (null i dette tilfellet ):
(3⋅xto - 7⋅x + 2) = (x -2) (3⋅x - 1) + 0
På denne måten var det mulig å faktorisere polynomet P (x), det vil si å skrive som et produkt av polynomer, det opprinnelige polynomet:
(3⋅xto - 7⋅x + 2) = (x -2) (3⋅x - 1)
- Eksempel 2
La polynomet Q (x) = x3 - x + 2. Vi vil vite om det er delbart med binomialet (x + 1).
Den mest direkte måten er å bare anvende faktorsetningen. I dette tilfellet må vi bare sjekke om x = -1 avbryter eller ikke polynomet Q (x).
Vi fortsetter ved å erstatte:
Q (-1) = (-1)3 - (-1) + 2 = -1 + 1 + 2 = 2
Resultatet er forskjellig fra null, derfor forsikrer faktorsetningen oss om at polynomet Q (x) ikke er delbart med (x + 1), siden Q (-1) ≠ 0.
Nå skal vi fortsette å utføre delingen av Q (x) med binomialet (x + 1) som en metode for verifisering av konklusjonen vår.
Ved denne anledningen vil inndelingen utføres ved hjelp av den syntetiske inndelingsmetoden, som består i å plassere i første rad bestilt fra høyeste grad til null grad alle koeffisientene til polynomet, inkludert de manglende, siden de har null koeffisient.
Så i den første kolonnen er den uavhengige termen til deleren plassert, men med tegnet endret, i vårt tilfelle er deleren (x + 1). Den uavhengige betegnelsen er 1, men som i den første kolonnen er den plassert endret tegn, det vil si -1.
Følgende figur illustrerer hvordan den syntetiske inndelingen gjøres:

Med dette resultatet blir det bekreftet at (x + 1) ikke er en faktor for polynomet Q (x) = x3 - x + 2 siden resten ikke er null.
Denne konklusjonen er ikke overraskende, fordi den allerede var spådd med faktorsetningen. Vær også oppmerksom på at når du erstatter x = -1 i Q (x), er det som er oppnådd nøyaktig resten eller resten av divisjonen av polynomer, siden Q (-1) = resten = 2.
Selvfølgelig gir inndelingen tilleggsinformasjonen til kvotienten C (x) = xto - x.
Husk at utbyttet Q (x) er lik divisoren (x + 1) med kvotienten C (x) pluss resten r = 2, har vi utvidelsen av polynomet Q (x) som følger:
Q (x) = (x + 1) (xto - x) + 2 = x (x + 1) (x - 1) + 2
Det skal bemerkes at dette uttrykket ikke er faktoriseringen av nevnte polynom, siden det er en ikke-nullbetegnelse, som er nøyaktig resten av verdi 2..
Opplæring
- Øvelse 1
Finn faktorene til polynomet
P (x) = x3 - 5 xto + 2 x + 8
Og skriv også din faktorisering.
Løsning
Faktorsetningen forteller oss at vi må se etter røttene til for deretter å finne faktorene (x - til), i dette tilfellet da det er et polynom av grad tre, må det være tre røtter.
Ettersom det er et polynom med heltallskoeffisienter, må røttene være mellom divisorene til det uavhengige begrepet, som i dette tilfellet er 8. Disse divisorene er:
± 1, ± 2, ± 4, ± 8.
Vi starter med å utforske +1: P (+1) = 13 - 5⋅ 1to + 2⋅1 + 8 = 1-5 + 2 + 8 = 6 som er forskjellig fra 0, derfor er +1 ikke en rot.
Vi utforsker -1:
P (-1) = (-1)3 - 5⋅ (-1)to + 2⋅ (-1) + 8 = -1 - 5 - 2 + 8 = 0
Fra resultatet konkluderes det at -1 er roten til P (x) og (x - (-1)) = (x + 1) er en faktor for polynomet.
To faktorer gjenstår å finne:
Vi beviser følgende som er +2:
P (+2) = (+2)3 - 5⋅ (+2)to + 2⋅ (+2) + 8 = 8 + (-20) + 4 + 8 = 0
Igjen får vi null. Så den andre faktoren er (x - 2).
Siden det er et polynom av grad tre, trenger vi bare å finne en faktor. Nå tester vi verdien +4 for å finne ut om den avbryter polynomet:
P (+4) = (+4)3 - 5⋅ (+4)to + 2⋅ (+4) + 8 = 64 - 80 + 8 + 8 = 0.
Det vil si at +4 er roten til P (x), og derfor er binomialet (x - 4) en annen av faktorene.
Ikke mer søk, fordi det er et polynom av grad 3 som har høyst tre røtter. I denne øvelsen viste alle røttene seg å være ekte og heltall.
Derfor blir polynomet P (x) fakturert slik:
P (x) = x3 - 5 xto + 2 x + 8 = (x + 1) (x - 2) (x - 4).
- Øvelse 2
La polynomet være p⋅x3 - x + 2p. Bestem verdien av p slik at polynomet kan deles med (x + 2).
Løsning
Vi bruker faktorteoremet, som sier at hvis x = -2 avbryter polynomet, så er (x - (-2)) en faktor for nevnte polynom..
Deretter erstatter vi x for (-2) i det opprinnelige polynomet, forenkler det og setter det lik null:
p⋅ (-2)3 - (-2) + 2p = 8p + 2 + 2p = 10p + 2 = 0
Nå er verdien på p ryddet slik at likheten til null er oppfylt:
p = -2 / 10 = -⅕
Dette betyr at polynomet:
-⅕⋅x3 - x - ⅖
Det er delbart med (x + 2), eller hva som tilsvarer: (x + 2) er en av faktorene.
Referanser
- Baldor Aurelio. Algebra. Grupo Redaksjonell Patria.
- Demana, W. Precalculus: Grafisk, numerisk, algebraisk 7. utg. Pearson Education.
- Jiménez, R. 2008. Algebra. Prentice hall.
- Stewart, J. 2006. Precalculus: Mathematics for Calculus. 5. Utgave. Cengage læring.
- Zill, D. 1984. Algebra og trigonometri. Mcgraw hill.



Ingen har kommentert denne artikkelen ennå.