De Den grunnleggende teoremet for regning sier at ethvert naturlig tall større enn 1 kan spaltes som et produkt av primtall - noen kan gjentas - og denne formen er unik for det tallet, selv om rekkefølgen på faktorene kan være forskjellig.
Husk at et primtall s Det er den som bare innrømmer seg selv og 1 som positive delere. Følgende tall er primtall: 2, 3, 5, 7, 11, 13 og så videre, siden det er uendelig. Nummer 1 regnes ikke som primtall, fordi det har en enkelt skiller.
For deres del blir tallene som ikke overholder ovennevnte ringt sammensatte tall, som 4, 6, 8, 9, 10, 12, 14 ... La oss ta tallet 10 for eksempel, og umiddelbart ser vi at det kan spaltes som et produkt av 2 og 5:
10 = 2 × 5
Både 2 og 5 er effektivt primtall. Teoremet sier at dette er mulig for hvilket som helst tall n:
Hvor s1, sto, s3... sr er primtall og k1, kto, k3,... kr de er naturlige tall. Så primtallene fungerer som mursteinene der, ved multiplikasjon, de naturlige tallene er bygget.
Artikkelindeks
Vi begynner med å vise at hvert tall kan spaltes til hovedfaktorer. La være et naturlig tall n> 1, prim eller kompositt.
For eksempel hvis n = 2, kan det uttrykkes som: 2 = 1 × 2, som er prim. På samme måte fortsett med følgende tall:
3 = 1 × 3
4 = 2 × 2
5 = 1 × 5
6 = 2 × 3
7 = 1 × 7
8 = 2 × 2 × 2
Vi fortsetter slik og dekomponerer alle naturlige tall til vi når tallet n -1. La oss se om vi kan gjøre det med følgende nummer: n.
Hvis n er prim, kan vi spalte den som n = 1 × n, men anta at n er sammensatt og har en divisor d, logisk mindre enn n:
1< d < n.
Hvis n / d = p1, med P1 et primtall, så skrives n som:
n = s1.d
Hvis d er primær, er det ikke noe mer å gjøre, men hvis det ikke er det, er det et tall nto som er en divisor av d og mindre enn dette: nto < d, por lo que d podrá escribirse como el producto de nto med et annet primtall sto:
d = sto nto
At når du bytter ut i det opprinnelige nummeret, ville n gi:
n = s1 .sto .nto
Anta nå at nto enten er et primtall, og vi skriver det som produktet av et primtall p3, av en divisor av deg n3, slik at n3 < nto < n1 < n:
nto = s3.n3 → n = s1 sto s3.n3
Vi gjentar denne prosedyren et begrenset antall ganger til vi oppnår:
n = s1.sto.s3 ... sr
Dette betyr at det er mulig å spalte alle sammen hele tall fra 2 til n, som et produkt av primtall.
La oss nå bekrefte at bortsett fra rekkefølgen til faktorene, er denne nedbrytningen unik. Anta at n kan skrives på to måter:
n = s1.sto.s3 ... sr = q1.hvato.hva3... hvas (med r ≤ s)
Selvfølgelig det1, hvato, hva3... er også primtall. Som s1 del a (q1.hvato.hva3... hvas) Så s1 er lik noen av "q", betyr det ikke noe til hvilken, så vi kan si at s1 = q1. Vi deler n med s1 og vi får:
sto.s3 ... sr =.hvato.hva3... hvas
Vi gjentar fremgangsmåten til vi deler alt med sr, så får vi:
1 = qr + 1... hvas
Men det er ikke mulig å komme til hvar + 1... hvas = 1 når r < s, solo si r = s. Aunque al admitir que r = s, también se admite que los “p” y los “q” son los mismos. Por lo tanto la descomposición es única.
Som vi har sagt tidligere, representerer primtallene, hvis du vil, atomene til tallene, deres grunnleggende komponenter. Så den grunnleggende teoremet for regning har mange bruksområder, den mest åpenbare: vi kan jobbe lettere med store tall hvis vi uttrykker dem som et produkt av mindre tall..
På samme måte kan vi finne den største felles multiple (LCM) og den største felles divisor (GCF), en prosedyre som hjelper oss å lage summer av brøk lettere, finne røtter av store tall, eller operere med radikaler, rasjonalisere og løse applikasjonsproblemer av svært mangfoldig karakter.
Videre er primtall ekstremt gåtefulle. Et mønster er ennå ikke gjenkjent i dem, og det er ikke mulig å vite hvilken som kommer neste. Den største hittil ble funnet av datamaskiner og har 24.862.048 sifre, selv om de nye primtallene vises sjeldnere hver gang.
Cicadas, cicádidos eller cicadas som bor nordøst i USA dukker opp i sykluser på 13 eller 17 år. De er begge primtall.
På denne måten unngår sikadene å falle sammen med rovdyr eller konkurrenter som har andre fødselsperioder, og heller ikke de forskjellige variantene av kikader konkurrerer med hverandre, siden de ikke sammenfaller i løpet av samme år..
Primtall brukes i kryptografi for å holde kredittkortinformasjonen hemmelig når du kjøper over Internett. På denne måten kommer dataene som kjøperen kommer nøyaktig til butikken uten å gå seg vill eller falle i hendene på skruppelløse mennesker..
Hvordan? Dataene på kortene er kodet i et tall N som kan uttrykkes som produktet av primtall. Disse primtallene er nøkkelen som dataene avslører, men de er ukjente for publikum, de kan bare dekodes på nettet de er rettet til.
Å dekomponere et tall i faktorer er en enkel oppgave hvis tallene er små (se de løste øvelsene), men i dette tilfellet brukes primtall på 100 sifre som en nøkkel, som når du multipliserer dem gir mye større tall, hvis detaljerte nedbrytning innebærer en stor oppgave.
Nedbryt 1029 til hovedfaktorer.
1029 kan deles med 3. Det er kjent fordi summen er et multiplum av 3: 1 + 0 + 2 + 9 = 12 når du legger til sifrene. 12. Da faktorenes rekkefølge ikke endrer produktet, kan vi starte der:
1029 3
343
1029 = 3 × 343
På den annen side 343 = 73, deretter:
1029 = 3 × 73 = 3 × 7 × 7 × 7
Og siden både 3 og 7 er primtall, er dette nedbrytningen av 1029.
Faktor trinomial xto + 42x + 432.
Trinomialet blir omskrevet i form (x + a). (x + b) og vi må finne verdiene til a og b, slik at:
a + b = 42; a.b = 432
Tallet 432 blir spaltet i hovedfaktorer, og derfra velges den riktige kombinasjonen ved prøving og feiling slik at de tilførte faktorene gir 42.
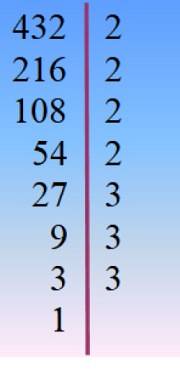
432 = 24 × 33 = 2 × 33× 23 = 24× 3to × 3 =…
Herfra er det flere muligheter for å skrive 432:
432 = 16 × 27 = 24 × 18 = 54 × 8 = 6 × 72 ... .
Og alle kan bli funnet ved å kombinere produkter mellom hovedfaktorene, men for å løse den foreslåtte øvelsen er den eneste egnede kombinasjonen: 432 = 24 × 18 siden 24 + 18 = 42, deretter:
xto + 42x + 432 = (x + 24). (x +18)
Ingen har kommentert denne artikkelen ennå.