
Trapesformede scaleneegenskaper, formler og ligninger, eksempler
EN trapes scalene er en polygon med fire sider, hvorav to er parallelle med hverandre, og med sine fire indre vinkler av forskjellige mål.
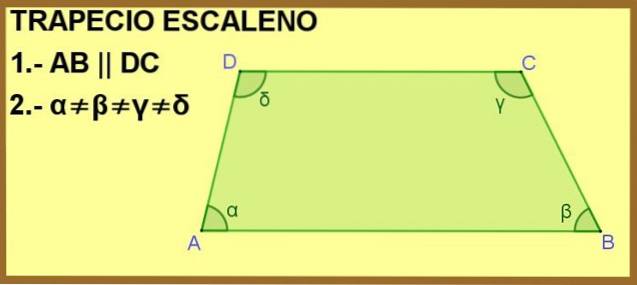
Den firsidede ABCD er vist nedenfor, der sidene AB og DC er parallelle med hverandre. Dette er nok til å gjøre det til en trapes, men i tillegg er de indre vinklene α, β, γ og δ forskjellige, derfor er trapesen scalene.
Artikkelindeks
- 1 Elementer av scalene trapes
- 1.1 Andre trapeser
- 2 eiendommer
- 3 Formler og ligninger
- 3.1 Høyde
- 3.2 Median
- 3.3 Diagonaler
- 3.4 Omkrets
- 3.5 Område
- 3.6 Andre forhold for scalene trapes
- 4 Konstruksjon av scalene trapes med linjal og kompass
- 5 Eksempel
- 5.1 - Løsning a
- 5.2 - Løsning b
- 6 Øvelse løst
- 6.1 Løsning
- 7 Referanser
Elementer av scalene trapes
Her er de mest karakteristiske elementene:
-Baser og sider: de parallelle sidene av trapesformet er dens baser, og de to ikke-parallelle sidene er sidene.
I en scalene trapes er basene av forskjellige lengder og de laterale også. Imidlertid kan en scalene trapesform ha en lateral like lang lengde som en base..
-Median: er segmentet som slutter seg til midtpunktene til sidene.
-Diagonaler: diagonalen til en trapes er segmentet som forbinder to motsatte hjørner. En trapes har, som hver firkant, to diagonaler. I den scalene trapesformen har de forskjellige lengder.
Andre trapeser
I tillegg til scalene trapes, er det andre spesielle trapeser: høyre trapes og den likebenede trapes..
En trapes er et rektangel når en av vinklene er riktig, mens en likbenet trapes har sidene av samme lengde.
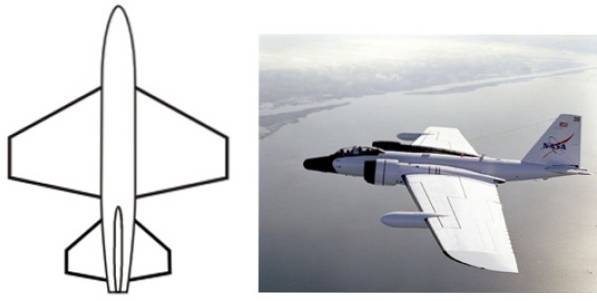
Den trapesformede formen har mange bruksområder på design- og industrinivå, for eksempel i konfigurasjonen av flyvinger, formen på hverdagsgjenstander som bord, stolrygg, emballasje, vesker, tekstilutskrifter og mer..
Eiendommer
Oppført nedenfor er egenskapene til den scalene trapesen, hvorav mange strekker seg til de andre typene trapes. I det følgende, når vi snakker om "trapes", vil eiendommen være anvendelig for alle typer, inkludert scalene..
1. Medianen til trapesformet, det vil si segmentet som forbinder midtpunktene til de ikke-parallelle sidene, er parallelt med noen av basene.
2. - Medianen til en trapes har en lengde som er halvsummen av basene og kutter diagonalene i midtpunktet.
3.- Diagonalene til en trapes skjæres på et punkt som deler dem i to seksjoner som er proporsjonale med kvotientene til basene.
4.- Summen av kvadratene til diagonalene til en trapes er lik summen av kvadratene på sidene pluss det doble produktet av basene..
5.- Segmentet som knytter seg til midtpunktene til diagonalene har en lengde som er lik halvformasjonen til basene.
6. - Vinklene ved siden av sidene er supplerende.
7.- I en scalene trapes er lengden på diagonalene forskjellige.
8. - En trapes har bare en innskrevet omkrets hvis summen av basene er lik summen av sidene.
9.- Hvis en trapes har en innskrevet omkrets, er vinkelen med toppunktet i midten av omkretsen og sidene som passerer gjennom endene på siden av trapesen rett.
10.- En scalene trapes har ikke en begrenset omkrets, den eneste typen trapes som har en er likebenne.
Formler og ligninger
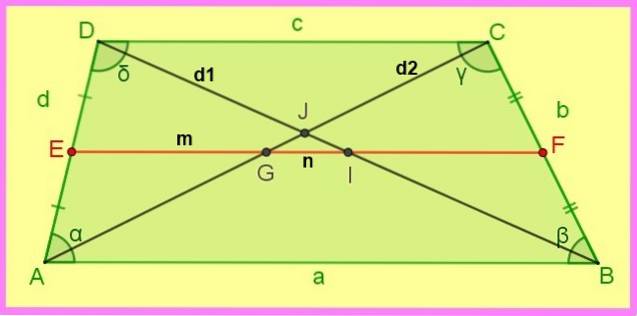
Følgende forhold til den scalene trapes er referert til følgende figur.
1.- Hvis AE = ED og BF = FC → EF || AB og EF || DC.
2.- EF = (AB + DC) / 2 det vil si: m = (a + c) / 2.
3.- DI = IB = d1 / 2 og AG = GC = dto /to.
4.- DJ / JB = (c / a) på samme måte CJ / JA = (c / a).
5.- DBto + ACto = ADto + F.Kr.to + 2 AB ∙ DC
Tilsvarende:
d1to + dtoto = dto + bto + 2 a ∙ c
6.- GI = (AB - DC) / 2
Nemlig:
n = (a - c) / 2
7.- α + δ = 180⁰ og β + γ = 180⁰
8.- Hvis α ≠ β ≠ γ ≠ δ så er d1 ≠ d2.
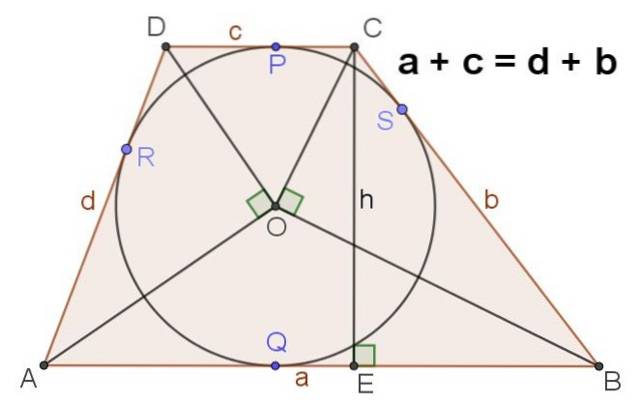
9.- Figur 4 viser en scalene trapesform som har en påskrevet omkrets, i dette tilfellet er det sant at:
a + c = d + b
10.- I en scalene trapesformet ABCD med en innskrevet omkrets av sentrum O, gjelder også følgende:
∡AOD = ∡BOC = 90⁰
Høyde
Høyden på en trapes er definert som segmentet som går fra et punkt av basen vinkelrett på den motsatte basen (eller til forlengelsen).
Alle trapesens høyder har samme måling h, så det meste av tiden refererer ordet høyde til målingen. I syntese er høyden avstanden eller skillet mellom basene.
Høyden h kan bestemmes ved å kjenne lengden på den ene siden og den ene vinkelen ved siden av siden:
h = d Sen (α) = d Sen (γ) = b Sen (β) = b Sen (δ)
Median
Tiltaket m til trapesens median er halvsummen av basene:
m = (a + b) / 2
Diagonaler
d1 = √ [ato + dto - 2 ∙ a ∙ d ∙ Cos (α)]
dto= √ [ato + bto - 2 ∙ a ∙ b ∙ Cos (β)]
Det kan også beregnes hvis bare lengden på trapesen er kjent:
d1 = √ [bto + a ∙ c - a (bto - dto) / (a - c)]
dto = √ [dto + a ∙ c - a (dto - bto) / (a - c)]
Omkrets
Omkretsen er den totale lengden på konturen, det vil si summen av alle sidene:
P = a + b + c + d
Område
Området til en trapes er semisummen av basene multiplisert med høyden:
A = h ∙ (a + b) / 2
Det kan også beregnes hvis medianen m og høyde h er kjent:
A = m ∙ h
Hvis bare lengden på sidene av trapesformen er kjent, kan området bestemmes ved hjelp av Herons formel for trapesformet:
A = [(a + c) / | a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]
Hvor s er semiperimeter: s = (a + b + c + d) / 2.
Andre forhold for scalene trapes
Krysset mellom medianen og diagonalene og parallellen som går gjennom skjæringen mellom diagonalene gir opphav til andre forhold.
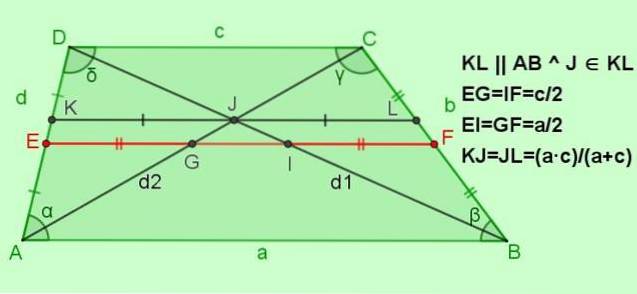
-Forhold for median EF
EF = (a + c) / 2; EG = IF = c / 2; EI = GF = a / 2
-Forhold for segmentet parallelt med basene KL, og passerer gjennom punktet J krysset mellom diagonalene
Hvis KL || AB || DC med J ∈ KL, deretter KJ = JL = (a ∙ c) / (a + c)
Konstruksjon av scalene trapes med linjal og kompass
Gitt lengdebunnene til Y c, hvor a> c og med sider av lengdene b og d, å være b> d, fortsett med å følge disse trinnene (se figur 6):
1.- Med regelen tegnes segmentet av major AB.
2.- Fra A se og på AB er punktet P merket slik at AP = c.
3.- Med kompasset med sentrum ved P og radius d tegnes en bue.
4. - Sentrer ved B med radius b og tegner en bue som avlyser buen som ble tegnet i forrige trinn. Vi kaller Q skjæringspunktet.
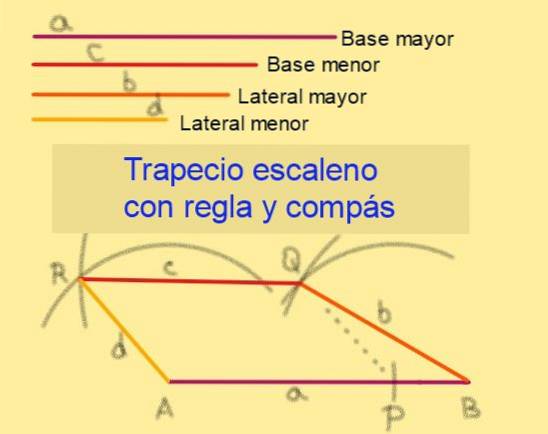
5.- Med sentrum på A, tegne en bue med radius d.
6. - Med sentrum ved Q, tegner du en bue med radius c som avskjærer buen tegnet i forrige trinn. Avskjæringspunktet vil bli kalt R.
7.- Segmentene BQ, QR og RA spores med linjalen.
8.- Kvadrilateralt ABQR er en scalene trapes, siden APQR er et parallellogram som garanterer at AB || Qr.
Eksempel
Følgende lengder er gitt i cm: 7, 3, 4 og 6.
a) Bestem om det med dem er mulig å konstruere en scalene trapesform som kan omskrive en sirkel.
b) Finn omkretsen, arealet, lengden på diagonalene og høyden på trapesformet, samt radiusen til den innskrevne sirkelen.
- Løsning til
Ved å bruke segmentene med lengde 7 og 3 som baser og de med lengde 4 og 6 som lateraler, kan en scalene trapesform konstrueres ved å bruke fremgangsmåten beskrevet i forrige avsnitt.
Det gjenstår å sjekke om den har en innskrevet omkrets, men husk eiendommen (9):
En trapes har bare en innskrevet omkrets hvis summen av basene er lik summen av sidene.
Vi ser det effektivt:
7 + 3 = 4 + 6 = 10
Da er vilkåret for eksistens av innskrevet omkrets oppfylt.
- Løsning b
Omkrets
Omkretsen P oppnås ved å legge til sidene. Siden basene legger opp til 10 og sidene også, er omkretsen:
P = 20 cm
Område
For å bestemme området, bare kjent på sidene, brukes forholdet:
A = [(a + c) / | a-c |] ∙ √ [(s-a) (s-c) (s-a-d) (s-a-b)]
Hvor s er semiperimeter:
s = (a + b + c + d) / 2.
I vårt tilfelle er semiperimeter verdt s = 10 cm. Etter å ha erstattet de respektive verdiene:
a = 7 cm; b = 6 cm; c = 3 cm; d = 4 cm
Rester:
A = [10/4] √ [(3) (7) (- 1) (- 3)] = (5/2) √63 = 19,84 cm².
Høyde
Høyden h er relatert til området A ved følgende uttrykk:
A = (a + c) ∙ h / 2, hvorfra høyden kan oppnås ved å fjerne:
h = 2A / (a + c) = 2 * 19,84 / 10 = 3,988 cm.
Radius av den innskrevne sirkelen
Radien til den innskrevne sirkelen er lik halvparten av høyden:
r = h / 2 = 1,984 cm
Diagonaler
Til slutt er lengden på diagonalene funnet:
d1 = √ [bto + a ∙ c - a (bto - dto) / (a - c)]
dto = √ [dto + a ∙ c - a (dto - bto) / (a - c)]
Ved å erstatte verdiene riktig har vi:
d1 = √ [6to + 7 ∙ 3 - 7 (6to - 4to) / (7 - 3)] = √ (36 + 21-7 (20) / 4) = √ (22)
dto = √ [4to + 7 ∙ 3 - 7 (4to - 6to) / (7 - 3)] = √ (16 + 21-7 (-20) / 4) = √ (72)
Det vil si: d1 = 4,69 cm og dto = 8,49 cm
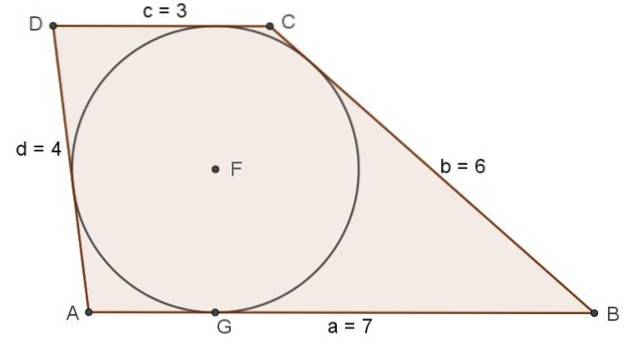
Treningen løst
Bestem de indre vinklene til trapesformet med baser AB = a = 7, CD = c = 3 og sidevinkler BC = b = 6, DA = d = 4.
Løsning
Kosinosetningen kan brukes for å bestemme vinklene. For eksempel blir vinkelen ∠A = α bestemt fra trekanten ABD med AB = a = 7, BD = d2 = 8,49 og DA = d = 4.
Kosinosetningen brukt på denne trekanten ser slik ut:
dtoto = ato + dto - 2 ∙ a ∙ d ∙ Cos (α), det vil si:
72 = 49 + 16-56 ∙ Cos (α).
Løsningen for er cosinus for vinkel α oppnådd:
Cos (α) = -1/8
Det vil si, α = ArcCos (-1/8) = 97,18⁰.
På samme måte oppnås de andre vinklene, deres verdier er:
β = 41,41⁰; γ = 138,59⁰ og til slutt δ = 82,82⁰.
Referanser
- C. E. A. (2003). Element av geometri: med øvelser og geometri av kompasset. University of Medellin.
- Campos, F., Cerecedo, F. J. (2014). Matematikk 2. Grupo Editorial Patria.
- Freed, K. (2007). Oppdag polygoner. Referanseutdanningsfirma.
- Hendrik, V. (2013). Generelle polygoner. Birkhäuser.
- IGER. (s.f.). Matematikk Første semester Tacaná. IGER.
- Jr. geometri. (2014). Polygoner. Lulu Press, Inc..
- Miller, Heeren & Hornsby. (2006). Mathematics: Reasoning And Applications (Tiende utgave). Pearson Education.
- Patiño, M. (2006). Matematikk 5. Redaksjonell Progreso.
- Wikipedia. Trapes. Gjenopprettet fra: es.wikipedia.com



Ingen har kommentert denne artikkelen ennå.