Isosceles trapesformede egenskaper, forhold og formler, eksempler

EN trapes likebent er en firkant der to av sidene er parallelle med hverandre, og dessuten har de to vinklene ved siden av en av de parallelle sidene samme mål.

I figur 1 har vi den firsidede ABCD, der sidene AD og BC er parallelle. I tillegg har vinklene ∠DAB og ∠ADC ved siden av den parallelle siden AD samme mål α. 

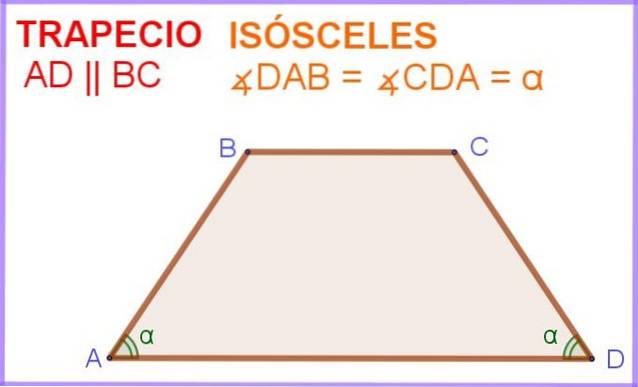
Så dette firsidige eller firesidige polygonet er i virkeligheten en likbenet trapes.

I en trapes kalles de parallelle sidene baser og ikke-parallellene kalles lateral. En annen viktig funksjon er høyde, som er avstanden som skiller de parallelle sidene.

I tillegg til den likebenede trapesen er det andre typer trapesformet:

-Tskalen havfisk, som har alle sine forskjellige vinkler og sider.

-Trektangel havfisk, der en lateral har rett tilstøtende vinkler.

Den trapesformede formen er vanlig i forskjellige felt innen design, arkitektur, elektronikk, beregning og mange flere, som det vil sees senere. Derfor er det viktig å bli kjent med egenskapene.

Artikkelindeks

• 1 eiendommer
  • 1.1 Eksklusiver av den likebenede trapesen
  • 1.2 For alle trapeser
• 2 Relasjoner og formler
  • 2.1 Unike forhold mellom den likebenede trapesen
  • 2.2 Forhold for enhver trapes
  • 2.3 Forhold for likbenet trapes med påskrevet omkrets
  • 2.4 Formler for å bestemme den ene siden, kjenne de andre og en vinkel
  • 2.5 Bestemmelse av den ene siden, å kjenne de andre og en diagonal
  • 2.6 Basen fra høyde, areal og annen base
  • 2.7 Kjente sidebaser, areal og vinkel
  • 2.8 Kjent sidemedian, areal og vinkel
  • 2.9 Kjent høyde på sidene
  • 2.10 Kjent høyde i vinkel og to sider
  • 2.11 Kjente diagonaler på alle sider, eller to sider og en vinkel
  • 2.12 Omkrets av likebenet trekant 
  • 2.13 Areal av ligebenet trapes
  • 2.14 Radius av den omskrevne sirkelen
• 3 Eksempler på bruk av den likebenede trapesen
  • 3.1 I arkitektur og konstruksjon
  • 3.2 I design
• 4 Løst øvelser
  • 4.1 - Øvelse 1
  • 4.2 - Øvelse 2
• 5 Referanser

Eiendommer

Eksklusivt for den likebenede trapesen

Hvis en trapes er likbenet, har den følgende karakteristiske egenskaper:

1.- Sidene har samme mål.

2.- Vinklene ved siden av basene er like.

3.- Motsatte vinkler er supplerende.

4.- Diagonalene har samme lengde, de to segmentene som forbinder motsatte hjørner er de samme.

5.- Vinkelen som dannes mellom basene og diagonalene er alle av samme mål.

6.- Den har en begrenset omkrets.

Omvendt, hvis en trapesform oppfyller noen av de ovennevnte egenskapene, er den en likebenet trapesform.

Hvis en av vinklene er like (lik 90 °) i en likeben trapesform, vil også alle de andre vinklene være rette og danne et rektangel. Det vil si at et rektangel er et spesielt tilfelle av ligebenet trapes.

For all trapes

Følgende sett med egenskaper er gyldig for enhver trapes:

7.- The median av trapeset, det vil si segmentet som forbinder midtpunktene til de ikke-parallelle sidene, er parallelt med noen av basene.

8.- Lengden på medianen er lik semisummen (summen delt på 2) av dens baser.

9.- Medianen til en trapes skjærer diagonalene på midtpunktet.

10. - Diagonalene til en trapes skjærer seg på et punkt som deler dem i to seksjoner proporsjonalt med kvotientene i basene.

11. - Summen av kvadratene til diagonalene til en trapes er lik summen av kvadratene på sidene pluss det doble produktet av basene.

12.- Segmentet som forbinder midtpunktene til diagonalene, har en lengde som er lik halvforskjellen til basene.

13. - Vinklene ved siden av sidene er supplerende.

14. - En trapes har en innskrevet omkrets hvis og bare hvis summen av basene er lik summen av sidene.

15.- Hvis en trapes har en innskrevet omkrets, er vinklene med toppunkt i midten av omkretsen og sidene som passerer gjennom endene på samme side rett vinkler.

Forhold og formler

Følgende sett med relasjoner og formler refererer til figur 3, der i tillegg til ligebenet trapes er det også vist viktige segmenter som allerede er nevnt, slik som diagonaler, høyde og median.

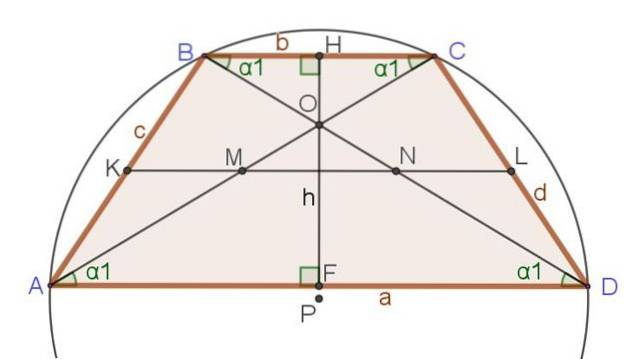
Unike forhold mellom den likebenede trapesen

1.- AB = DC = c = d

2.- ∡DAB = ∡CDA og ∡ABC = ∡BCD

3.- ∡DAB + ∡BCD = 180º og ∡CDA + ∡ABC = 180º

4.- BD = AC

5.- ∡CAD = ∡BDA = ∡CBD = ∡BCA = α₁

6.- A, B, C og D tilhører den omskrevne sirkelen.

Forhold for enhver trapes

7. Hvis AK = KB og DL = LC ⇒ KL || AD og KL || F.Kr.

8.- KL = (AD + BC) / 2

9.- AM = MC = AC / 2 og DN = NB = DB / 2

10.- AO / OC = AD / BC og DO / OB = AD / BC

11. - AC^to + DB^to = AB^to + DC^to + 2⋅AD⋅BC

12.- MN = (AD - BC) / 2

13.- ∡DAB + ∡ABC = 180º og ∡CDA + ∡BCD = 180º

14.- Hvis AD + BC = AB + DC ⇒ ∃ R enn like langt fra AD, BC, AB og DC

15.- Hvis ∃ R er like langt fra AD, BC, AB og DC, så:

∡BRA = ∡DRC = 90º

Forhold for likbenet trapes med påskrevet omkrets

Hvis summen av basene i en likebent trapesform er lik to ganger en lateral, så er den innskrevne omkretsen.

Følgende egenskaper gjelder når den likebenede trapes har en innskrevet omkrets (se figur 4 ovenfor):

16.- KL = AB = DC = (AD + BC) / 2

17. - Diagonalene krysses i rette vinkler: AC ⊥ BD

18.- Høyden måler det samme som medianen: HF = KL, det vil si h = m.

19.- Kvadratet av høyden er lik produktet av basene: h^to = BC⋅AD

20.- Under disse spesifikke forholdene er trapesformens areal lik kvadratet av høyden eller produktet av basene: Areal = h^to = BC⋅AD.

Formler for å bestemme den ene siden, kjenne de andre og en vinkel

Kjent en base, den laterale og en vinkel, den andre basen kan bestemmes av:

a = b + 2c Cos α

b = a - 2c Cos α

Hvis lengden på basene og en vinkel er gitt som kjent data, er lengden på begge sider:

c = (a - b) / (2 Cos α)

Bestemmelse av den ene siden, å kjenne de andre og en diagonal

a = (d₁^to - c^to) / b;

b = (d₁^to - c^to)/ til 

c = √ (d₁^to - a⋅b)

Hvor₁ er lengden på diagonalene.

Base fra høyde, areal og annen base

a = (2 A) / t - b

b = (2 A) / t - a

Kjente sidebunner, areal og vinkel

c = (2A) / [(a + b) sin α]

Kjent sidemedian, areal og vinkel

c = A / (m sin α)

Kjent høyde på sidene

h = √ [4 c^to - (a - b)^to]

Kjent høyde en vinkel og to sider

h = tg α⋅ (a - b) / 2 = c. sin α

Kjente diagonaler på alle sider, eller to sider og en vinkel

d₁ = √ (c^to+ a b)

d₁ = √ (a^to+ c^to - 2 a c Cos α)

d₁ = √ (b^to + c^to- 2 b c Cos β)

Omkretsen av den likebenede trekanten 

P = a + b + 2c

Isosceles trapesområde

Det er flere formler for å beregne området, avhengig av hvilke data som er kjent. Følgende er best kjent, avhengig av underlag og høyde:

A = h⋅ (a + b) / 2

Og du kan også bruke disse andre:

-Hvis sidene er kjent

A = [(a + b) / 4] √ [4c^to - (a - b)^to]

-Når du har to sider og en vinkel

A = (b + c Cos α) c Sen α = (a - c Cos α) c Sen α

-Hvis radiusen til den innskrevne sirkelen og en vinkel er kjent

A = 4 r^to / Sen α = 4 r^to / Sen β

-Når basene og en vinkel er kjent

A = a⋅b / Sen α = a⋅b / Sen β 

-Hvis trapesformet kan skrives inn en omkrets

A = c⋅√ (a⋅b) = m⋅√ (a⋅b) = r⋅ (a + b) / 2

-Kjente diagonalene og vinkelen de danner med hverandre

A = (d₁^to/ 2) Sen γ = (d₁^to / 2) Sen δ 

-Når du har lateral, median og en vinkel

A = mc.sen α = mc.sen β

Radius av den omskrevne sirkelen

Bare likebenede trapeser har en begrenset omkrets. Hvis den større basen a, er lateral c og diagonal d kjent₁, da er radiusen R av sirkelen som passerer gjennom trapesens fire hjørner:

R = a⋅c⋅d₁ / 4√ [p (p -a) (p -c) (p - d₁)]

Hvor p = (a + c + d₁) / to

Eksempler på bruk av likebenet trapes

Den likebenede trapesen vises i designfeltet, som vist i figur 2. Og her er noen flere eksempler:

I arkitektur og konstruksjon

De gamle inkaene kjente den likebenede trapesen og brukte den som et bygningselement i dette vinduet i Cuzco, Peru:

Og her vises trapesen igjen i samtalen trapesformet ark, et materiale som ofte brukes i konstruksjonen:

I design

Vi har allerede sett at den likebenede trapesen vises i hverdagsgjenstander, inkludert mat som denne sjokoladestangen:

Løst øvelser

- Øvelse 1

En likebenet trapes har en base større enn 9 cm, en base mindre enn 3 cm og diagonalene 8 cm hver. Regne ut:

a) Side

b) Høyde

c) Omkrets

d) Område

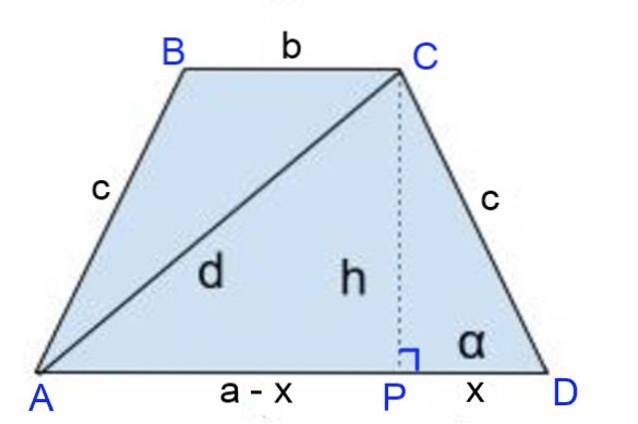
Løsning til

Høyden CP = h er tegnet, der høydefoten definerer segmentene:

PD = x = (a-b) / 2 y 

AP = a - x = a - a / 2 + b / 2 = (a + b) / 2.

Bruke Pythagoras teorem til høyre trekant DPC:

c^to = h^to + (a - b)^to / 4

Og også til høyre trekant APC:

d^to = h^to + AP^to = h^to + (a + b)^to / 4

Til slutt, medlem for medlem, blir den andre ligningen trukket fra den første og forenklet:

d^to - c^to = ¼ [(a + b)^to - (a-b)^to] = ¼ [(a + b + a-b) (a + b-a + b)]

d^to - c^to = ¼ [2a 2b] = a b

c^to= d^to - a b ⇒ c = √ (d^to - a b) = √ (8^to - 9⋅3) = √37 = 6,08 cm

Løsning b

h^to = d^to - (a + b)^to / 4 = 8^to - (12^to / to^to ) = 8^to - 6^to = 28

h = 2 √7 = 5,29 cm

Løsning c

Omkrets = a + b + 2 c = 9 + 3 + 2⋅6,083 = 24,166 cm

Løsning d

Areal = h (a + b) / 2 = 5,29 (12) / 2 = 31,74 cm

- Øvelse 2

Det er en likebenet trapesform som har den største basen to ganger den minste og den minste basen er lik høyden, som er 6 cm. Bestemme seg for:

a) Lengden på lateral

b) Omkrets

c) Område

d) Vinkler

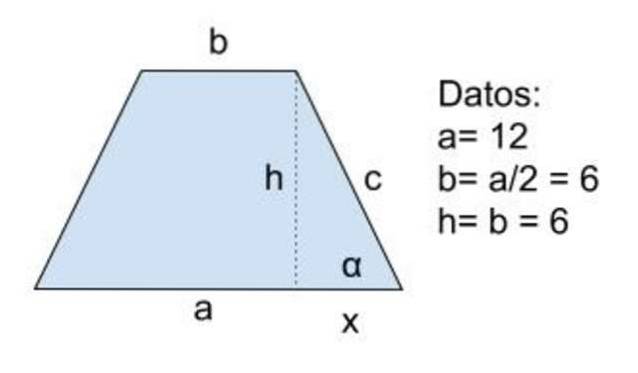
Løsning til

Data: a = 12, b = a / 2 = 6 og h = b = 6

Vi fortsetter på denne måten: høyden h er tegnet og den pythagoreiske teoremet blir brukt på hypotenus-trekanten "c" og bena h og x:

c^to = h^to+xc^to

Da må du beregne verdien av høyden ut fra dataene (h = b) og den på benet x: 

a = b + 2 x ⇒ x = (a-b) / 2

Erstatter de tidligere uttrykkene vi har:

c^to = b^to+(a-b)^to/to^to

Nå er de numeriske verdiene introdusert, og det er forenklet:

c^to = 62+ (12-6) 2/4

c^to = 62 (1 + ¼) = 62 (5/4)

Å skaffe:

c = 3√5 = 6,71 cm

Løsning b

Omkretsen P = a + b + 2 c

P = 12 + 6 + 6√5 = 6 (8 + √5) = 61,42 cm

Løsning c

Området som en funksjon av høyden og lengden på basene er:

A = h⋅ (a + b) / 2 = 6⋅ (12 + 6) / 2 = 54 cm^to

Løsning d

Vinkelen α dannet av lateral med større base oppnås ved trigonometri:

Brunbrun (α) = h / x = 6/3 = 2

α = ArcTan (2) = 63,44º

Den andre vinkelen, den som danner den laterale med den mindre basen, er β, som er supplerende til α:

β = 180º - α = 180º - 63.44º = 116.56º

Referanser

1. E. A. 2003. Elementer av geometri: med øvelser og kompassgeometri. University of Medellin.
2. Campos, F. 2014. Matematikk 2. Grupo Editorial Patria.
3. Freed, K. 2007. Oppdag polygoner. Referanseutdanningsfirma.
4. Hendrik, V. 2013. Generaliserte polygoner. Birkhäuser.
5. IGER. Matematikk Første semester Tacaná. IGER.
6. Jr. geometri. 2014. Polygoner. Lulu Press, Inc..
7. Miller, Heeren & Hornsby. 2006. Matematikk: resonnement og applikasjoner. 10. Utgave. Pearson Education.
8. Patiño, M. 2006. Matematikk 5. Redaksjonell Progreso.
9. Wikipedia. Trapes. Gjenopprettet fra: es.wikipedia.com