De akutte trekanter er de hvis tre indre vinkler er spisse vinkler; det vil si at målingen på hver av disse vinklene er mindre enn 90 ° grader. Ved ikke å ha noen rett vinkel, har vi at den pythagoreiske teorem ikke holder for denne geometriske figuren.
Derfor, hvis vi ønsker å ha noen form for informasjon om noen av sidene eller vinklene, er det nødvendig å gjøre bruk av andre teoremer som tillater oss å få tilgang til nevnte data. De vi kan bruke er sinussetningen og kosinussetningen.
Artikkelindeks
Blant egenskapene som denne geometriske figuren har, kan vi markere de som er gitt av det enkle faktum å være en trekant. Blant disse har vi:
- En trekant er en polygon som har tre sider og tre vinkler.
- Summen av de tre indre vinklene er lik 180 °.
- Summen av to av sidene er alltid større enn den tredje.
Som et eksempel, la oss se på følgende trekant ABC. På en generell måte identifiserer vi sidene med små bokstaver og vinklene med store bokstaver, på en slik måte at den ene siden og den motsatte vinkelen har samme bokstav.
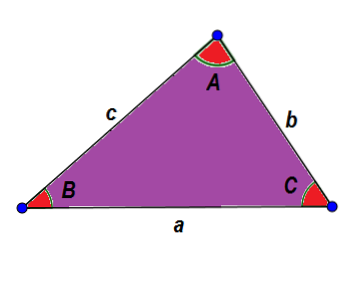
Fra egenskapene som allerede er gitt, vet vi at:
A + B + C = 180 °
a + b> c, a + c> b og b + c> a
Hovedkarakteristikken som skiller denne typen trekant fra resten er at, som vi allerede nevnte, dens indre vinkler er akutte; det vil si at målet på hver av vinklene er mindre enn 90 °.
Akutte trekanter, sammen med stumpe trekanter (de der en av deres vinkler har et mål større enn 90 °), er en del av settet med skrå trekanter. Dette settet består av trekanter som ikke er rette vinkler.
Ettersom de skrå trekantene er en del, må vi kunne løse problemer som involverer akutte trekanter, vi må benytte oss av sinesetningen og kosinussetningen.
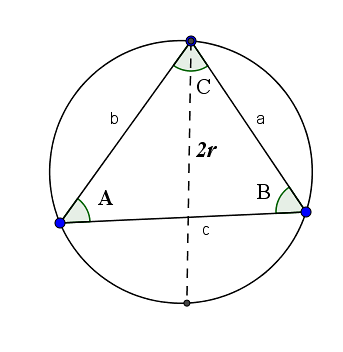
Sinussetningen forteller oss at forholdet mellom en side og sinusen til den motsatte vinkelen er lik dobbelt så stor radius av sirkelen som er dannet av de tre hjørnene i trekanten. Nemlig:
2r = a / sin (A) = b / sin (B) = c / sin (C)
På den annen side gir kosinussetningen oss disse tre likhetene for hvilken som helst trekant ABC:
tilto= bto + cto -2bc * cos (A)
bto= ato + cto -2ac * cos (B)
cto= ato + bto -2ab * cos (C)
Disse setningene er også kjent som henholdsvis sinusloven og cosinusloven..
Et annet kjennetegn vi kan gi av de akutte trekantene er at to av disse er like hvis de oppfyller et av følgende kriterier:
- Hvis de har alle tre like sider.
- Hvis de har en side og to like vinkler til hverandre.
- Hvis de har to like sider og en vinkel.
Vi kan klassifisere akutte trekanter basert på deres sider. Disse kan være:
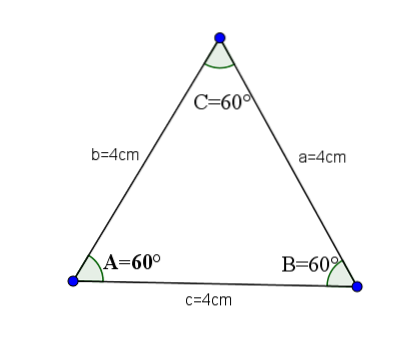
De er de akutte trekantene som har alle sidene like, og derfor har alle deres indre vinkler samme verdi, som er A = B = C = 60 ° grader.
La oss som et eksempel ta følgende trekant, hvis sider a, b og c har verdien 4.
Disse trekantene, i tillegg til å ha akutte indre vinkler, har den karakteristikken at de har to av deres like sider, og den tredje, som vanligvis blir tatt som base, er forskjellig.
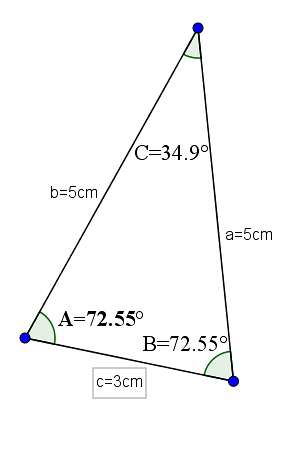
Et eksempel på denne typen trekant kan være en hvis base er 3 og de andre to sidene har verdien 5. Med disse målene vil den ha motsatte vinkler til like sider med verdien 72,55 ° og motsatt vinkel på basen ville være 34,9 °.
Dette er trekantene som alle har forskjellige sider to og to. Derfor er alle vinklene i tillegg til å være mindre enn 90 ° forskjellige fra to til to.
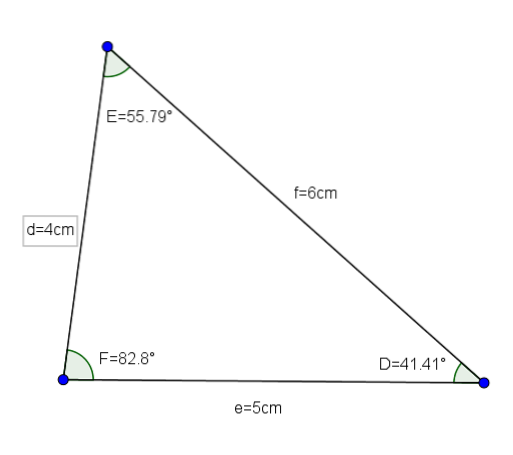
Trekanten DEF (hvis mål er d = 4, e = 5 og f = 6 og dens vinkler er D = 41,41 °, E = 55,79 ° og F = 82,8 °) er et godt eksempel på en akutt trekantskala.
Som vi sa før, for å løse problemer som involverer akutte trekanter, er det nødvendig å bruke sinus- og cosinussetningene.
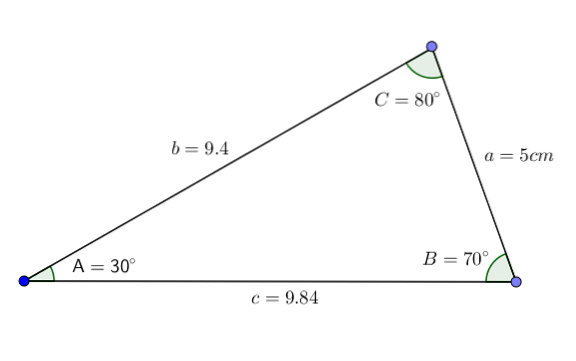
Gitt en trekant ABC med vinkler A = 30 °, B = 70 ° og side a = 5 cm, vil vi vite verdien av vinkel C og sider b og c.
Det første vi gjør er å bruke det faktum at summen av de indre vinklene til en trekant er 180 °, for å oppnå verdien av vinkelen C.
180 ° = A + B + C = 30 ° + 70 ° + C = 100 ° + C
Vi rydder C og vi sitter igjen med:
C = 180 ° - 100 ° = 80 °
Siden vi allerede kjenner til de tre vinklene og den ene siden, kan vi bruke sinesetningen til å bestemme verdien av de gjenværende sidene. Etter teoremet har vi:
a / sin (A) = b / sin (B) og a / sin (A) = c / (sin (C)
Vi isolerer b fra ligningen, og vi sitter igjen med:
b = (a * sin (B)) / sin (A) ≈ (5 * 0,940) / (0,5) ≈ 9,4
Nå trenger vi bare å beregne verdien av c. Vi går frem på samme måte som i forrige sak:
c = (a * sin (C)) / sin (A) ≈ (5 * 0,984) / (0,5) ≈ 9,84
Dermed får vi alle dataene i trekanten. Som vi kan se, faller denne trekanten i kategorien scalene akutt trekant.
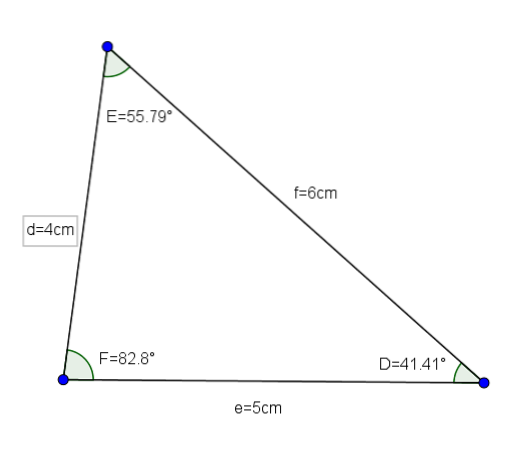
Gitt en trekant DEF med sidene d = 4 cm, e = 5 cm og f = 6 cm, vil vi vite verdien av vinklene til nevnte trekant.
For dette tilfellet vil vi bruke cosinusloven, som forteller oss at:
dto= eto + Fto - 2efcos (D)
Fra denne ligningen kan vi løse cos (D), som gir oss som et resultat:
Cos (D) = ((4)to - (5)to -(6)to) / (- 2 * 5 * 6) = 0,75
Derfor har vi D≈ 41,41 °
Nå bruker vi senomsetningen vi har følgende ligning:
d / (sin (D) = e / (sin (E)
Å løse synden (E) har vi:
sin (E) = e * sin (D) / d = (5 * 0,66) / 4 ≈ 0,827
Derfor har vi E≈55,79 °
Til slutt bruker vi at summen av de indre vinklene til en trekant er 180 °, har vi den F that82.8 °.
Ingen har kommentert denne artikkelen ennå.