
Balansering av vektorberegning, eksempler, øvelser
De balanserende vektor Det er den som er i motsetning til den resulterende vektoren og derfor er i stand til å balansere et system, siden det har samme størrelse og samme retning, men motsatt retning av dette.
Ved mange anledninger refererer balanseringsvektoren til en kraftvektor. For å beregne balanseringskraften, finn først den resulterende kraften, som vist i følgende figur:
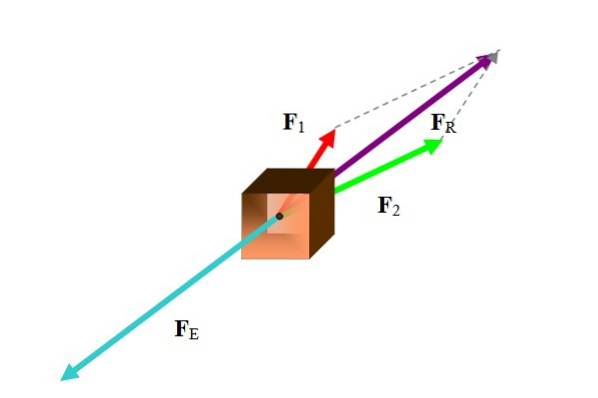
Det er forskjellige metoder for å utføre denne oppgaven, avhengig av dataene som foreligger. Siden kreftene er vektorer, er den resulterende vektorsummen av de deltakende kreftene:
FR = F1 + Fto + F3 + ... .
Blant metodene som skal brukes er grafiske metoder som polygonal, parallellogram og analytiske metoder som nedbrytning av krefter i deres kartesiske komponenter. I eksemplet brukte figuren parallellogrammetoden.
Når den resulterende kraften er funnet, er balanseringskraften akkurat den motsatte vektoren.
Ja FOG er balanseringskraften, så er den fornøyd med det FOG brukes på et visst punkt, garanterer det translasjonell likevekt i systemet. Hvis det er en enkelt partikkel, vil den ikke bevege seg (eller kanskje den gjør med konstant hastighet), men hvis det er et utvidet objekt, vil det fortsatt ha muligheten til å rotere:
FR + FOG = 0
Artikkelindeks
- 1 Eksempler
- 1.1 Tvinge bord
- 2 Løst øvelser
- 2.1-Øvelse 1
- 2.2-Øvelse 2
- 3 Referanser
Eksempler
Balanseringskrefter er til stede overalt. Vi er selv balansert av kraften som stolen utøver for å kompensere for vekten. Objektene som er i ro: bøker, møbler, taklamper og et stort antall mekanismer balanseres kontinuerlig av krefter.
For eksempel balanseres en bok i ro på et bord av den normale kraften den utøver på boka, og forhindrer at den faller. Det samme skjer med kjeden eller kabelen som holder lampen hengende fra taket i et rom. Kablene som holder en last fordeler vekten gjennom spenningen i dem.
I en væske er noen gjenstander i stand til å flyte og forbli i ro, siden vekten deres balanseres av en oppadgående kraft utøvd av væsken, kalt trykk.
Ulike mekanismer må balanseres, vel vitende om balanseringskraftvektoren som stenger, bjelker og søyler.
Når du bruker en skala, er det nødvendig å balansere gjenstandens vekt med en kraft som er ekvivalent, enten ved å legge til vekter eller ved hjelp av fjærer..
Tving bord
Krafttabellen brukes i laboratoriet for å bestemme balanseringskraften. Den består av en sirkulær plattform, som du har ovenfra i figuren, og som har en vinkelmåler for å måle vinkler.
På kantene av bordet er det trinser gjennom hvilke tau som holder vekter passerer og som konvergerer i en ring som er i midten.
For eksempel henges to vekter. Spenningene som genereres i strengene av disse vektene er tegnet i rødt og blått i figur 2. En tredje vekt i grønt kan balansere den resulterende kraften til de to andre og holde systemet i balanse..
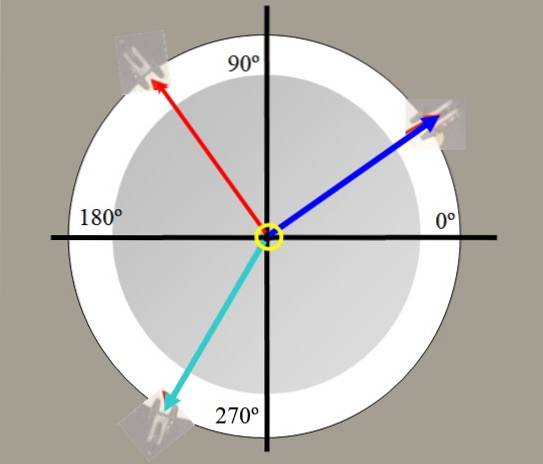
Med styrketabellen er det mulig å verifisere kreftens vektorkarakter, spalte krefter, finne balanseringskraften og verifisere Lamys teorem:
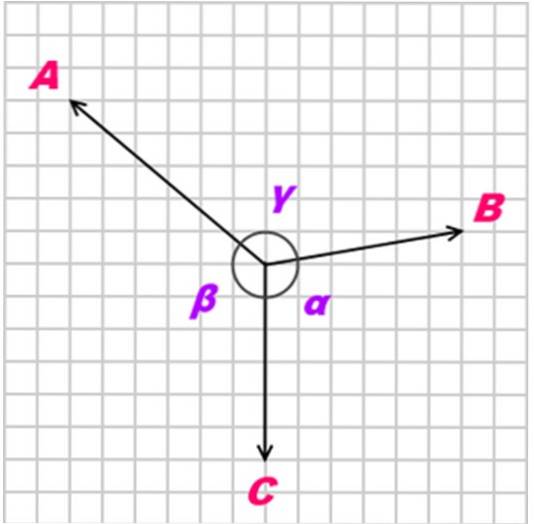
Hvis en kroppen er i likevekt takket være tre koplanære krefter, samtidig og ikke-kollinær (ikke parallell), kalt TIL, B Y C, forholdet mellom disse kreftene er som følger:
A / sin α = B / sin β = C / sin γ
Løst øvelser
-Øvelse 1
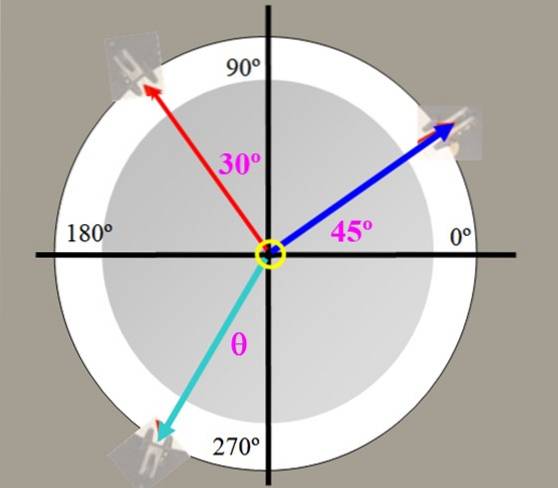
225 g (blå spenning) og 150 g (rød spenning) vekter henges på kraftbordet i figur 2, med vinklene vist. Finn verdien av balanseringskraften og vinkelen den gir med den vertikale aksen.
Løsning
Problemet kan arbeides med vektene uttrykt i gram (krefter). La P1 = 150 gram og P.to = 225 gram, de respektive komponentene i hver er:
P1x = 225. cos 45 ° g = 159,10 g; P1 år = 225. cos 45º g = 159,10 g
P2x = -150. sin 30 g = -75,00 g; P2 og = 150. cos 30º g = 129,90 g
Den resulterende vekten PR er funnet ved algebraisk å legge til komponentene:
PRx = 159,10 - 75,00 g = 84,10 g
PRy = 159,10 + 129,90 g = 289,00 g
Balansevekten POG er vektoren motsatt PR:
PTidligere = -84,10 g
PHei = -289,00 g
Størrelsen på balansvekten beregnes av:
POG = (STidligereto + PHeito)1/2 = ((-84,10)to + (-289,00)to)1/2 g = 301 g
Vinkelen θ i figuren er:
θ = arctg (-84.10 / -289.00) = 16.2º i forhold til aksen Y negativ.
-Øvelse 2
Finn balanseringsvektoren til systemet vist i figuren, vel vitende om at hvert kvadrat måler 10 m på en side.
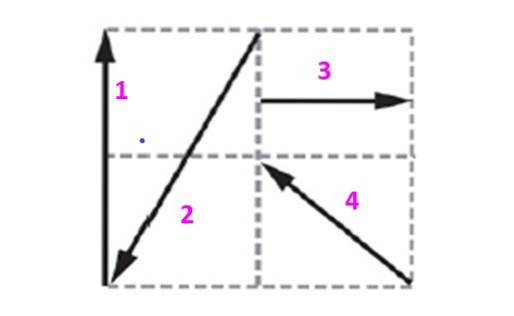
Løsning
Vektorene i dette rutenettet vil uttrykkes i form av enhets- og ortogonale vektorer Jeg Y j som bestemmer flyet. Vektor 1, som vil bli betegnet som v1 den har styrke 20 m og er rettet vertikalt oppover. Det kan uttrykkes som:
v1 = 0 Jeg +tjue j m
Fra tegningen kan det sees at vektor 2 er:
vto = -10 Jeg - tjue j m
Vektor 3 er horisontal og peker i positiv retning:
v3 = 10 Jeg + 0 j m
Til slutt helles vektor 4 45 °, siden den er diagonalen på firkanten, derfor måler komponentene dens samme:
v4 = -10 Jeg + 10 j m
Merk at skiltene indikerer mot hvilken side av aksen komponentene er: over og til høyre har et + tegn, mens under og til venstre har de et tegn -.
Den resulterende vektoren oppnås ved å legge komponent til komponent:
vR = -10 Jeg + 10 j m
Da er balanseringsvektoren til systemet:
vOG = 10 Jeg - 10 j m
Referanser
- Beardon, T. 2011. En introduksjon til vektorer. Hentet fra: nrich.maths.org.
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley. 38-52.
- Figueroa, D. Series: Physics for Sciences and Engineering. Volum 1. Kinematikk. 31-68.
- Fysisk. Modul 8: Vektorer. Gjenopprettet fra: frtl.utn.edu.ar
- Hibbeler, R. 2006. Mekanikk for ingeniører. Statisk. 6. utgave. Continental Publishing Company. 15-53.
- Vector Addition Calculator. Gjenopprettet fra: 1728.org
- Vektorer. Gjenopprettet fra: wikibooks.org



Ingen har kommentert denne artikkelen ennå.