
Vectors teamlenses definisjon, notasjon, øvelser
To eller flere vektorer er teamlinser hvis de har samme modul, samme retning og samme sans, selv om utgangspunktet er forskjellig. Husk at egenskapene til en vektor er nøyaktig: opprinnelse, modul, retning og sans.
Vektorer er representert med et orientert segment eller en pil. Figur 1 viser representasjonen av flere vektorer i planet, hvorav noen linser i henhold til definisjonen som ble gitt først..
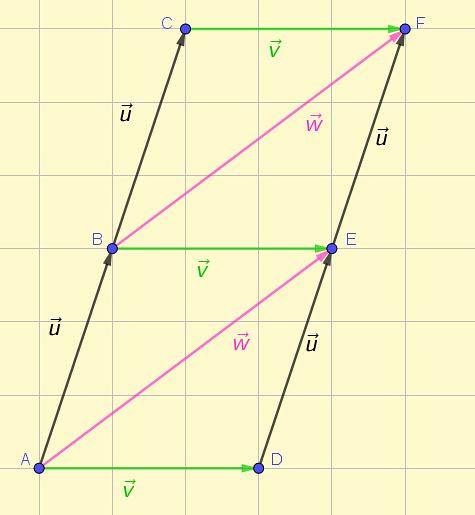
Ved første øyekast er det mulig å se at de tre grønne vektorene har samme størrelse, samme retning og samme sans. Det samme kan sies om de to rosa vektorene og de fire svarte vektorene.
Mange størrelser av naturen har en vektor-lignende oppførsel, slik er det hastighet, akselerasjon og kraft, for å nevne noen få. Derfor viktigheten av å karakterisere dem riktig.
Artikkelindeks
- 1 Merknad for vektorer og utstyr
- 1.1 Gratis, glidende og motsatte vektorer
- 2 Øvelser
- 2.1-Øvelse 1
- 2.2-Øvelse 2
- 2.3-Øvelse 3
- 3 Referanser
Merking for vektorer og utstyr
For å skille vektormengder fra skalære størrelser, brukes ofte den fet skrift eller en pil over bokstaven. Når du arbeider med vektorer for hånd, på den bærbare datamaskinen, er det nødvendig å skille dem med pilen, og når du bruker et trykt medium, brukes fet skrift.
Vektorer kan betegnes ved å angi utgangspunkt eller opprinnelse og ankomststed. For eksempel AB, F.Kr., FRA Y EF i figur 1 er vektorer, i stedet AB, F.Kr., FRA Y EF er skalære størrelser eller tall som indikerer størrelsen, modulen eller størrelsen på deres respektive vektorer.
For å indikere at to vektorer er teamorienterte, symbolet "∼ ". Med denne notasjonen kan vi i figuren påpeke følgende vektorer som er teamorienterte mot hverandre:
AB∼BC∼DE∼EF
De har alle samme størrelse, retning og mening. Derfor overholder de regelverket angitt ovenfor..
Gratis, glidende og motsatte vektorer
Alle vektorene i figuren (for eksempel AB) er representativt for settet med alle faste linsevektorer. Dette uendelige settet definerer klassen av gratisvektorer eller.
eller = AB, BC, DE, EF, ...
En alternativ notasjon er følgende:
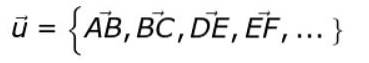
Hvis den dristige eller den lille pilen ikke er plassert over bokstaven eller, er at vi vil referere til vektormodulen eller.
Gratisvektorer brukes ikke til et bestemt punkt.
For deres del skyvevektorer De er teamlengdevektorer til en gitt vektor, men applikasjonspunktet må være inneholdt i handlingslinjen til den gitte vektoren.
Og motsatte vektorer De er vektorer som har samme størrelse og retning, men motsatte sanser, selv om de i engelske tekster kalles de motsatte retninger siden retningen også indikerer sansen. Motsatte vektorer er ikke team.
Opplæring
-Øvelse 1
Hvilke andre vektorer fra de som er vist i figur 1 er team-lense for hverandre??
Løsning
Bortsett fra de som allerede er angitt i forrige avsnitt, observeres det fra figur 1 at AD, VÆRE Y EC De er også teamlengdevektorer:
AD ∼ BE ∼ CE
Noen av dem er representative for klassen av gratisvektorer v.
Vektorene AE Y BF :
AE ∼ BF
Hvem er representanter for klassen w.
-Øvelse 2
Punktene A, B og C er på det kartesiske planet XY og deres koordinater er:
A = (- 4.1), B = (- 1.4) og C = (- 4, -3)
Finn koordinatene til et fjerde punkt D slik at vektorene AB Y CD være teamorientert.
Løsning
Så det CD være teamorientert AB må ha samme modul og samme adresse som AB .
Modulen AB kvadrat er:
|AB| ^ 2 = (-1 - (-4)) ^ 2 + (4 -1) ^ 2 = 9 + 9 = 18
Koordinatene til D er ukjente, så vi kan si: D = (x, y)
Så: |CD| ^ 2 = (x - (- 4)) ^ 2 + (y - (-3)) ^ 2
Som |AB| = |CD| er en av forutsetningene for AB Y CD vær teamorientert, du har:
(x + 4) ^ 2 + (y + 3) ^ 2 = 18
Siden vi har to ukjente, kreves det en annen ligning, som kan oppnås fra den betingelsen at AB Y CD er parallelle og i samme forstand.
Helling av vektor AB
Vektorhellingen AB angir adressen din:
Helling AB = (4 -1) / (- 1 - (-4)) = 3/3 = 1
Angir at vektoren AB 45º med X-aksen.
Vector CD skråning
Skråningen av CD beregnes på lignende måte:
Helling CD = (y - (-3)) / (x - (- 4)) = (y + 3) / (x + 4)
Likestiller dette resultatet med hellingen på AB vi har følgende ligning:
y + 3 = x + 4
Noe som betyr at y = x + 1.
Hvis dette resultatet erstattes av ligningen for modulene, har vi:
(x + 4) ^ 2 + (x + 1 + 3) ^ 2 = 18
Forenkling er fortsatt:
2 (x + 4) ^ 2 = 18,
Som tilsvarer:
(x + 4) ^ 2 = 9
Det vil si x + 4 = 3 som innebærer at x = -1. Så koordinatene til D er (-1, 0).
Sjekk
Komponentene i vektoren AB er (-1 - (- 4), 4 -1) = (3, 3)
og vektoren CD er (-1 - (- 4)); 0 - (- 3)) = (3, 3)
Noe som betyr at vektorene er teamorienterte. Hvis to vektorer har samme kartesiske komponenter, har de samme modul og retning, derfor er de teamlinser..
-Øvelse 3
Den gratis vektoren eller har styrke 5 og retning 143.1301º.
Finn deres kartesiske komponenter og bestem koordinatene til punkt B og C, vel vitende om at de faste vektorene AB og CD er teamorientert mot u. Koordinatene til A er (0, 0) og koordinatene til punkt C er (-3,2).
Løsning
Situasjonen som oppgaven gir, kan representeres av følgende figur:
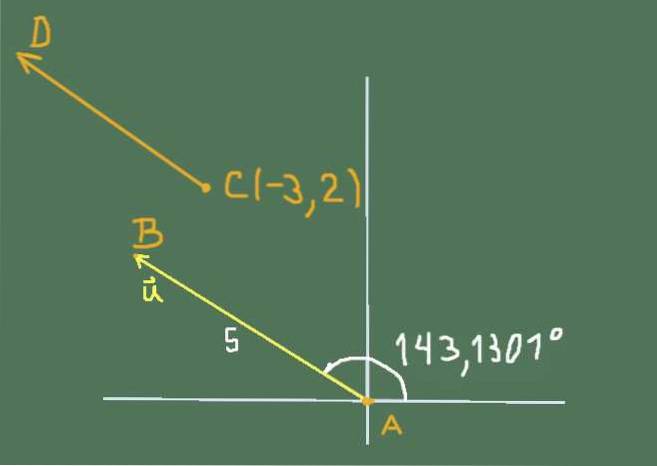
De kartesiske komponentene i eller De er
eller = (5 * cos (143.1301º); 5 * sin (143.1301º))
Å gjøre beregningene gjenstår:
eller = (-4,3)
Koordinatene til B er ukjente, så vi vil plassere B (x, y)
Koordinatene til vektoren AB er (x-0; y-0), men siden u er team-linse, må likhet av komponenter oppfylles, det følger derfor at koordinatene til B er (-4, 3).
Tilsvarende koordinatene til vektoren CD er (x - (- 3)); (og - 2) at det må være teamorientert u, leller fører til:
x + 3 = -4 og y -2 = 3
Da blir koordinatene til punkt D (-7, 5).
Referanser
- Calculus.cc. Fast vektor. Gratis vektor. Gjenopprettet fra: calculo.cc
- Descartes 2d. Faste vektorer og gratis flyvektorer. Gjenopprettet fra: recursostic.educacion.es
- Guao-prosjekt. Vektorer teamlinser. Gjenopprettet fra: guao.org
- Resnick, R., Krane, K. (2001). Fysikk. New York: John Wiley & Sons.
- Serway, R.; Jewett, John W. (2004). Physics for Scientists and Engineers (6. utg.). Brooks / Cole.
- Tipler, Paul A. (2000). Fysikk for vitenskap og teknologi. Volum I. Barcelona: Ed. Reverté.
- Weisstein, E. "Vector." I Weisstein, Eric W. MathWorld. Wolfram Research.

Ingen har kommentert denne artikkelen ennå.