
Molar volumkonsept og formel, beregning og eksempler
De molar volum Det er en intensiv egenskap som indikerer hvor mye plass en mol av et bestemt stoff eller en forbindelse opptar. Det er representert med symbolet Vm, y uttrykkes i enheter av dm3/ mol for gasser, og cm3/ mol for væsker og faste stoffer, fordi sistnevnte er mer begrenset av sine høyere intermolekylære krefter.
Denne egenskapen er tilbakevendende når man studerer termodynamiske systemer som involverer gasser; siden ligningene for å bestemme V for væsker og faste stofferm de blir mer kompliserte og unøyaktige. Derfor, når det gjelder grunnleggende emner, er molarvolumet alltid assosiert med den ideelle gassteorien..
Dette skyldes det faktum at strukturelle aspekter er irrelevante for ideelle eller perfekte gasser; alle partiklene blir visualisert som kuler som elastisk kolliderer med hverandre og oppfører seg på samme måte uansett massene eller egenskapene deres.
Dette er tilfelle, en mol av enhver ideell gass vil oppta det samme volumet V ved et gitt trykk og temperaturm. Det sies da at en mol av en ideell gass under normale forhold på henholdsvis P og T, 1 atm og 0 ° C, vil oppta et volum på 22,4 liter. Denne verdien er nyttig og omtrentlig selv når man vurderer ekte gasser.
Artikkelindeks
- 1 Konsept og formel
- 1.1 For gasser
- 1.2 For væsker og faste stoffer
- 2 Hvordan beregne molar volum?
- 3 Eksempler på beregning av molarvolum
- 3.1 Eksempel 1
- 3.2 Øvelse 2
- 3.3 Øvelse 3
- 4 Referanser
Konsept og formel
For gasser
Den umiddelbare formelen for å beregne molarvolumet til en art er:
Vm = V / n
Hvor V er volumet den opptar, og n mengden av arten i mol. Problemet er at Vm avhenger av trykket og temperaturen som molekylene opplever, og et matematisk uttrykk som tar hensyn til disse variablene er ønsket.
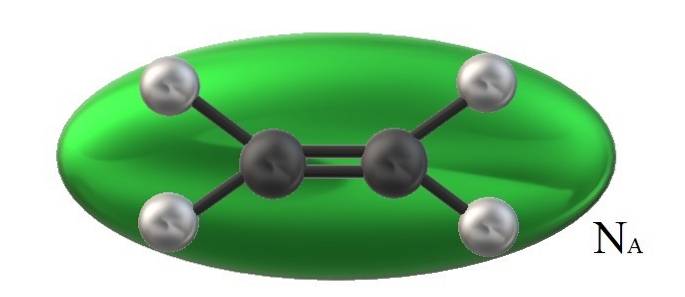
Etylenet på bildet, HtoC = CHto, den har et tilhørende molekylvolum begrenset av en grønn ellipsoid. Denne HtoC = CHto Den kan rotere på flere måter, som er som om nevnte ellipsoid ble flyttet i rommet for å visualisere hvor mye volum det ville okkupere (åpenbart ubetydelig).
Men hvis volumet av en slik grønn ellipsoid multipliserer vi den med NTIL, Avogadros nummer, vil vi da ha ett mol etylenmolekyler; en mol ellipsoider samhandler med hverandre. Ved høyere temperaturer vil molekylene skille seg fra hverandre; mens de er ved høyere trykk, vil de trekke seg sammen og redusere volumet.
Derfor har Vm er avhengig av P og T. Etylen har en plan geometri, så det kan ikke tenkes at dens Vm er nøyaktig og nøyaktig den samme som metan, CH4, av tetrahedral geometri og i stand til å bli representert med en kule og ikke en ellipsoid.
For væsker og faste stoffer
Molekylene eller atomer av væsker og faste stoffer har også sin egen Vm, som kan være omtrent relatert til dens tetthet:
Vm = m / (dn)
Temperatur påvirker molarvolum for væsker og faste stoffer mer enn trykk, så lenge sistnevnte ikke varierer kraftig eller er ublu (i størrelsesorden GPa). På samme måte, som nevnt med etylen, har geometriene og molekylære strukturer stor innflytelse på verdiene til Vm.
Imidlertid observeres det under normale forhold at tettheter for forskjellige væsker eller faste stoffer ikke varierer for mye i størrelsesorden; det samme gjelder molarvolumene. Merk at jo tettere de er, desto mindre vil V værem.
Når det gjelder faste stoffer, avhenger molarvolumet også av deres krystallinske strukturer (volumet av enhetscellen)..
Hvordan beregne molar volum?
I motsetning til væsker og faste stoffer er det en ligning som gjør det mulig for oss å beregne V for ideelle gasserm som en funksjon av P og T og deres endringer; dette er den av ideelle gasser:
P = nRT / V
Som er imøtekommende for å uttrykke V / n:
V / n = RT / P
Vm = RT / P
Hvis vi bruker gasskonstanten R = 0,082 L atm K-1Muldvarp-1, da skal temperaturene uttrykkes i kelvin (K), og trykket i atmosfærer. Merk at her kan vi se hvorfor Vm er en intensiv egenskap: T og P har ikke noe med gassens masse å gjøre, men med volumet.
Disse beregningene er bare gyldige under forhold der gasser oppfører seg nær idealiteten. Verdiene oppnådd ved eksperimentering har imidlertid en liten feilmargin i forhold til det teoretiske.
Eksempler på beregning av molarvolum
Eksempel 1
Det er en gass Y med densitet er 8,5 · 10-4 g / cm3. Hvis vi har 16 gram som tilsvarer 0,92 mol Y, beregner du molarvolumet.
Fra tetthetsformelen kan vi beregne hvilket volum av Y disse 16 gram opptar:
V = 16 g / (8,5 10-4 g / cm3)
= 18,823,52 cm3 eller 18,82 l
Så Vm Det beregnes direkte ved å dele dette volumet med antall mol gitt:
Vm = 18,82 L / 0,92 mol
= 20,45 L / mol eller L mol-1 eller dm3Muldvarp-1
Øvelse 2
I forrige eksempel på Y ble det ikke på noe tidspunkt spesifisert hva som var temperaturen som partiklene i gassen opplevde. Forutsatt at Y ble arbeidet med atmosfæretrykk, beregne temperaturen som er nødvendig for å komprimere den til det bestemte molare volumet.
Uttalelsen om øvelsen er lenger enn oppløsningen. Vi bruker ligningen:
Vm = RT / P
Men vi løser for T, og når vi vet at atmosfæretrykket er 1 atm, løser vi:
T = VmP / R
= (20,45 L / mol) (1 atm) / (0,082 L atm / K mol)
= 249,39 K
Det vil si at en mol Y vil oppta 20,45 liter ved en temperatur nær -23,76 ºC.
Øvelse 3
Etter de forrige resultatene, bestem Vm ved 0 ºC, 25 ºC og ved absolutt null ved atmosfærisk trykk.
Når vi transformerer temperaturene til kelvin, har vi først 273,17 K, 298,15 K og 0 K. Vi løser direkte ved å erstatte den første og andre temperaturen:
Vm = RT / P
= (0,082 L atm / K mol) (273,15 K) / 1 atm
= 22,40 L / mol (0 ºC)
= (0,082 L atm / K mol) (298,15 K) / 1 atm
= 24,45 L / mol (25 ° C)
Verdien på 22,4 liter ble nevnt i begynnelsen. Legg merke til hvordan Vm øker med temperaturen. Når vi ønsker å gjøre den samme beregningen med absolutt null, snubler vi over den tredje loven om termodynamikk:
(0,082 L atm / K mol) (0 K) / 1 atm
= 0 l / mol (-273,15 ºC)
Gass Y kan ikke ha et ikke-eksisterende molarvolum; det betyr at den har blitt transformert til en væske og den forrige ligningen ikke lenger er gyldig.
På den annen side er umuligheten av å beregne Vm ved absolutt null overholder den termodynamikkens tredje lov, som sier at det er umulig å avkjøle noe stoff til temperaturen på absolutt null.
Referanser
- Ira N. Levine. (2014). Prinsipper for fysisk-kjemi. Sjette utgave. Mc Graw Hill.
- Glasstone. (1970). Avhandling om fysisk kjemi. Andre utgave. Aguilar.
- Wikipedia. (2019). Molar volum. Gjenopprettet fra: en.wikipedia.org
- Helmenstine, Anne Marie, Ph.D. (8. august 2019). Molar Volum Definition in Chemistry. Gjenopprettet fra: thoughtco.com
- BYJU'S. (2019). Molar Volume Formula. Gjenopprettet fra: byjus.com
- González Monica. (28. oktober 2010). Molar volum. Gjenopprettet fra: quimica.laguia2000.com


Ingen har kommentert denne artikkelen ennå.