De fabrikkrigg Det er en enkel maskin som består av et arrangement av trinser med en multipliserende effekt av kraften. På denne måten kan en last løftes ved å påføre like mye som en brøkdel av vekten på den frie enden av tauet..
Den består av to sett med remskiver: en som er festet til en støtte og en annen som utøver den resulterende kraften på lasten. Remskivene er montert på en generelt metallisk ramme som holder dem.
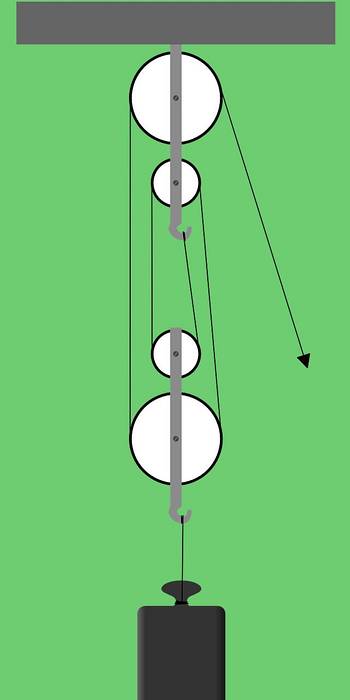
Figur 1 viser en fabrikkrigg bestående av to grupper med to remskiver hver. Denne typen trinsearrangement kalles også seriell rigging eller heiser.
Artikkelindeks
For å forstå hvorfor dette arrangementet multipliserer kraften som utøves, begynner vi med det enkleste tilfellet, som består av en fast remskive og en mobil remskive..
I figur 2 har vi en remskive A festet til taket ved hjelp av en støtte. Remskive A kan rotere fritt rundt sin akse. Vi har også en remskive B som har en brakett festet til remskiven, som lasten er plassert på. Remskive B, i tillegg til å kunne rotere fritt rundt sin akse, har muligheten til å bevege seg vertikalt.
Anta at vi er i en likevektssituasjon. Tenk på kreftene som virker på remskive B. Aksen til remskive B støtter en totalvekt P som er rettet nedover. Hvis dette var den eneste kraften på trinsen B, ville den falle, men vi vet at tauet som passerer gjennom denne trinsen også utøver to krefter, som er T1 og T2 som er rettet oppover..
For at det skal være translasjonell likevekt, må de to oppadgående kreftene være lik vekten støttet av remskiven B.
T1 + T2 = P
Men siden remskive B også er i rotasjonsvekt, så er T1 = T2. Kreftene T1 og T2 kommer fra spenningen som påføres strengen, kalt T.
Derfor er T1 = T2 = T. Ved å erstatte i forrige ligning forblir det:
T + T = P
2T = P
Noe som indikerer at spenningen på tauet bare er halvparten av vekten:
T = P / 2
For eksempel, hvis lasten var 100 kg, ville det være nok å bruke en kraft på 50 kg i tauets frie ende for å heve lasten med konstant hastighet..
La oss nå se på spenningene og kreftene som virker på en samling bestående av to anordninger av støtter A og B med to remskiver hver..
Støtte B har muligheten til å bevege seg vertikalt, og kreftene som virker på den er:
- Vekten P av lasten, peker loddrett nedover.
- To påkjenninger på den store remskiven og to påkjenninger på den lille remskiven. Totalt fire spenninger, som alle peker oppover.
For at det skal være translasjonell likevekt, er det nødvendig at kreftene som peker vertikalt opp, er likeverdige med belastningen som peker nedover. Det vil si at det må oppfylles:
T + T + T + T = P
Det vil si 4 T = P
Fra hvilket det følger at den påførte kraften T i den frie enden av tauet bare er en fjerdedel av vekten på grunn av lasten som vil løftes., T = P / 4.
Med denne verdien for spenningen T kan belastningen holdes statisk eller stige med konstant hastighet. Hvis en spenning større enn denne verdien ble påført, ville belastningen akselerere oppover, en tilstand som er nødvendig for å bringe den ut av hvile..
I henhold til det som er sett i de foregående tilfellene, er det for hver remskive i den mobile enheten et par oppadgående krefter som utøves av tauet som passerer gjennom remskiven. Men denne kraften kan ikke være noe annet enn spenningen på tauet i den frie enden.
Slik at for hver remskive i den mobile enheten vil det være en vertikal kraft oppover som er lik 2T. Men siden det er n trinser i den bevegelige enheten, følger det at den totale kraften som peker vertikalt oppover er:
2 n T
For at det skal være vertikal balanse, er det nødvendig at:
2 n T = P
derfor er kraften som påføres i den frie enden:
T = P / (2 n)
I dette tilfellet kan det sies at den utøvde kraften T multipliseres 2 n ganger på lasten.
For eksempel, hvis vi hadde en fabrikkrigg med 3 faste og 3 mobile remskiver, ville tallet n være lik 3. På den annen side, hvis lasten var P = 120 kg, ville kraften som ble påført i den frie enden være T = 120 kg / (2 * 3) = 20 kg.
Tenk på en faktorrigg som består av to faste remskiver og to bevegelige remskiver. Maksimum spenning tauet tåler er 60 kg. Bestem hva som er maksimal belastning som kan plasseres.
Når lasten hviler eller beveger seg med konstant hastighet, er dens vekt P relatert til spenningen T som påføres tauet ved hjelp av følgende forhold:
P = 2 n T
Siden det er en rigg med to mobile og to faste remskiver, så er n = 2.
Maksimal belastning som kan plasseres oppnås når T har størst mulig verdi, som i dette tilfellet er 60 kg.
Maksimal belastning = 2 * 2 * 60 kg = 240 kg
Finn forholdet mellom tauets spenning og vekten av lasten, i en faktorulle med to trinser der lasten akselereres med akselerasjon ved.
Forskjellen i dette eksemplet med hensyn til det som har blitt sett hittil er at dynamikken i systemet må vurderes. Så vi foreslår Newtons andre lov for å finne det etterspurte forholdet.
I figur 4 tegner vi kreftene på grunn av tauets spenning i gult. Den bevegelige delen av heisen har en total masse M. Vi tar som et referansesystem en på nivå med den første faste remskiven og positiv nedover.
Y1 er den laveste trinseakselposisjonen.
Vi bruker Newtons andre lov for å bestemme akselerasjonen a1 til den bevegelige delen av riggen:
-4 T + Mg = M al
Siden vekten av belastningen er P = Mg, hvor g er tyngdekraften, kan forholdet ovenfor skrives:
-4T + P = P (a1 / g)
Hvis vi ønsket å bestemme spenningen som ble påført tauet når en viss vektbelastning P akselereres med akselerasjon a1, ville det forrige forholdet se slik ut:
T = P (1 - a1 / g) / 4
Merk at hvis systemet var i ro eller beveget seg med konstant hastighet, så a1 = 0, og vi ville gjenopprette det samme uttrykket som vi fikk i tilfelle 2.
I dette eksemplet brukes samme rigging fra øvelse 1, med samme tau som støtter maksimalt 60 kg spenning. En viss belastning heves, og akselererer den fra hvile til 1 m / s på 0,5 s, ved å bruke maks tau. Finn lastens maksimale vekt.
Vi vil bruke uttrykkene oppnådd i øvelse 2 og referansesystemet i figur 4 der den positive retningen er loddrett ned.
Akselerasjonen av lasten er a1 = (-1 m / s - 0 m / s) / 0,5 s = -2 m / s ^ 2.
Vekten av lasten i kilo-kraft er gitt av
P = 4 T / (1 - a1 / g)
P = 4 * 60 kg / (1 + 2 / 9,8) = 199,3 kg
Dette er lastens maksimale vekt uten at tauet går i stykker. Vær oppmerksom på at verdien oppnådd er mindre enn den som er oppnådd i eksempel 1, hvor belastningen ble antatt å ha null akselerasjon, det vil si i ro eller med konstant hastighet..
Ingen har kommentert denne artikkelen ennå.