De aksiomer av sannsynlighet de er matematiske proposisjoner som henviser til teorien om sannsynlighet, som ikke fortjener bevis. Aksiomene ble etablert i 1933 av den russiske matematikeren Andrei Kolmogorov (1903-1987) i sitt arbeid Grunnleggende om sannsynlighetsteori og la grunnlaget for den matematiske studien av sannsynlighet.
Når du utfører et bestemt tilfeldig eksperiment ξ, er prøveområdet E settet med alle mulige resultater av eksperimentet, også kalt arrangementer. Enhver hendelse er betegnet som A og P (A) er sannsynligheten for at den skal forekomme. Da fastslår Kolmogorov at:
-Aksiom 1 (ikke negativitet): sannsynligheten for at en hendelse A skal forekomme er alltid positiv eller null, P (A) ≥0. Når sannsynligheten for en hendelse er 0, kalles den umulig hendelse.
-Axiom 2 (sikkerhet): når en hendelse som tilhører E, er sannsynligheten for at den forekommer 1, som vi kan uttrykke som P (E) = 1. Det er det som er kjent som en sikker hendelse, siden når du gjennomfører et eksperiment, er det med all sikkerhet et resultat.
-Axiom 3 (tillegg): i tilfelle to eller flere inkompatible hendelser to og to, kalt A1, TILto, TIL3…, Sannsynligheten for at hendelse A inntreffer1 pluss Ato pluss A3 og så videre er det summen av sannsynlighetene for at hver og en skjer separat.
Dette uttrykkes som: P (A1 U Ato U A3 U…) = P (A1) + P (A.to) + P (A.3) + ...
Artikkelindeks
Sannsynlighetsaksiomene er mye brukt i en rekke applikasjoner. For eksempel:
En thumbtack eller tack blir kastet i luften, og når den faller på gulvet er det mulighet for å lande med spissen opp (U) eller med spissen ned (D) (vi vil ikke vurdere andre muligheter). Eksempelområdet til dette eksperimentet består av disse hendelsene, deretter E = U, D.
Ved å bruke aksiomene har vi:
P (E) = 1 (Axiom 2)
Men P (E) = P (U) + P (D) (Aksiom 3), fordi disse hendelsene er gjensidig uforenlige, eller usammenhengende. Håndtaket faller ikke med tuppen opp eller ned samtidig, det er det ene eller det andre, men ikke begge deler, ettersom andre muligheter ikke vurderes. Deretter:
P (U) + P (D) = 1
P (U) = 1 - P (D)
Enten det er like sannsynlig å lande tipp opp eller peke ned, P (U) = P (D) = ½ (Aksiom 1). Det kan imidlertid være at konstruksjonen og utformingen av thumbtack er mer sannsynlig å falle på en eller annen måte. For eksempel kan det være det P (U) = ¾ samtidig som P (D) = ¼ (Aksiom 1).
Merk at summen av sannsynlighetene i begge tilfeller gir 1. Aksiomene indikerer imidlertid ikke hvordan sannsynlighetene skal tildeles, i det minste ikke helt. Men de bekrefter at de er tall mellom 0 og 1, og at, som i dette tilfellet, er summen av alle 1.
Sannsynlighetens aksiomer er ikke en metode for å tilordne verdien av sannsynligheten. For dette er det tre alternativer som er kompatible med aksiomene:
Hver hendelse tildeles samme sannsynlighet for å skje, og sannsynligheten for forekomst er definert som:
P (A) = antall saker gunstig for hendelse A / antall mulige saker
Hva er for eksempel sannsynligheten for å trekke et ess fra et kort med franske kort? Kortstokken har 52 kort, 13 av hver farge, og det er fire farger. Hver drakt har 1 ess, så totalt er det 4 ess:
P (as) = 4/52 = 1/13
Laplaces regel er begrenset til begrensede utvalgsområder, der hver hendelse er like sannsynlig.
Her må eksperimentet være repeterbart, siden metoden er basert på å utføre et stort antall repetisjoner..
La oss gjøre i repetisjoner av eksperimentet ξ, hvor vi finner at n er antall ganger en bestemt hendelse A inntreffer, og sannsynligheten for at denne hendelsen inntreffer er:
P (A) = limi → ∞ (ingen)
Hvor n / i er den relative frekvensen til en hendelse.
Å definere P (A) på denne måten tilfredsstiller Kolmogorovs aksiomer, men har den ulempen at mange tester må utføres for at sannsynligheten skal være passende.
En person eller en gruppe mennesker kan bli enige om å tildele sannsynligheten til en hendelse, gjennom egen vurdering. Denne metoden har ulempen at forskjellige mennesker kan tilordne forskjellige sannsynligheter til den samme hendelsen..
I eksperimentet med å kaste 3 ærlige mynter samtidig, skaff deg sannsynligheten for hendelsene som er beskrevet:
a) 2 hoder og en hale.
b) 1 hode og to haler
c) 3 kryss.
d) Minst 1 ansikt.
Hoder er betegnet med C og haler av X. Men det er flere måter å få to hoder og en hale på. For eksempel kan de to første myntene lande hoder og den tredje kan hale haler. Eller det første kan falle hoder, det andre halene og det tredje hodet. Og til slutt kan den første være haler og de gjenværende hodene.
For å svare på spørsmålene er det nødvendig å kjenne til alle mulighetene, som er beskrevet i et verktøy som heter tre diagram eller sannsynlighetens tre:
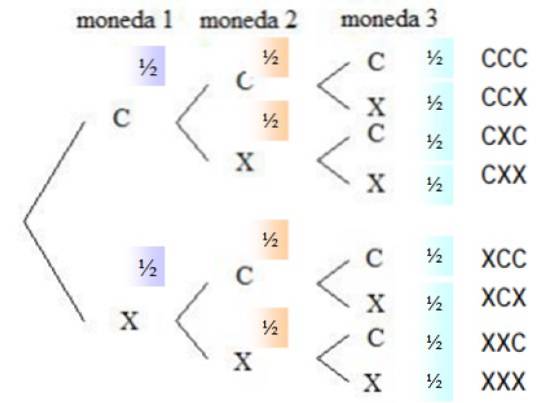
Sannsynligheten for at en hvilken som helst mynt kommer ut av hodet er ½, det samme gjelder haler, siden mynten er ærlig. I høyre kolonne er oppført alle mulighetene som kastet har, det vil si prøveområdet.
Fra prøveområdet velges kombinasjonene som svarer på den forespurte hendelsen, siden rekkefølgen ansiktene vises ikke er viktig. Det er tre gunstige begivenheter: CCX, CXC og XCC. Sannsynligheten for at hver hendelse skjer er:
P (CCX) = ½. ½. ½ = 1/8
Det samme skjer for CXC- og XCC-hendelsene, hver har en 1/8 sannsynlighet for å skje. Derfor er sannsynligheten for å få nøyaktig 2 hoder summen av sannsynligheten for alle gunstige hendelser:
P (2-sidig) = 1/8 + 1/8 + 1/8 = 3/8 = 0,375
Å finne sannsynligheten for at nøyaktig to kryss forekommer er et problem som er analogt med det forrige. Det er også tre gunstige hendelser hentet fra prøveområdet: CXX, XCX og XXC. Derfor:
P (2 kryss) = 3/8 = 0,375
Intuitivt vet vi at sannsynligheten for å få 3 haler (eller 3 hoder) er lavere. I dette tilfellet er den etterspurte hendelsen XXX, på slutten av høyre kolonne, hvis sannsynlighet er:
P (XXX) = ½. ½. ½ = 1/8 = 0,125.
Det bes om å få minst 1 ansikt, dette betyr at 3 ansikter, 2 ansikter eller 1 ansikt kan komme ut. Den eneste hendelsen som er uforenlig med dette er den der tre haler kommer ut, hvis sannsynlighet er 0,125. Derfor er sannsynligheten som søkes:
P (minst 1 hode) = 1 - 0,125 = 0,875.
Ingen har kommentert denne artikkelen ennå.