Ortonnormale basisegenskaper, eksempler og øvelser

EN ortonormal base Den er dannet med vektorer vinkelrett på hverandre og hvis modul også er 1 (enhetsvektorer). La oss huske at en base B i et vektorrom V, er definert som et sett med lineært uavhengige vektorer som er i stand til å generere nevnte rom.

I sin tur er et vektorrom en abstrakt matematisk enhet der elementene er vektorer, vanligvis assosiert med fysiske størrelser som hastighet, kraft og forskyvning eller også med matriser, polynomer og funksjoner..

Vektorer har tre karakteristiske elementer: størrelse eller modul, retning og sans. Et ortonormalt grunnlag er spesielt nyttig for å representere og operere med dem, siden enhver vektor som tilhører et bestemt vektorrom V, kan skrives som en lineær kombinasjon av vektorene som danner det ortonormale grunnlaget.

På denne måten utføres operasjoner mellom vektorer analytisk, slik som addisjon, subtraksjon og de forskjellige typer produkter definert i nevnte rom..

Blant de mest brukte basene i fysikk er basen dannet av enhetsvektorer Jeg, j Y k De representerer de tre særegne retningene til det tredimensjonale rommet: høyde, bredde og dybde. Disse vektorene er også kjent som kanoniske enhetsvektorer.

Hvis vektorene i stedet bearbeides i et plan, vil to av disse tre komponentene være tilstrekkelig, mens for en-dimensjonale vektorer bare en kreves.

Artikkelindeks

• 1 Egenskapene til basene
• 2 Eksempler på baser
  • 2.1 Det kanoniske grunnlaget i ℜ n
  • 2.2 Det kanoniske grunnlaget på ℜ3
  • 2.3 Andre ortonormale baser i ℜ3
• 3 Løst øvelser
  • 3.1 - Øvelse 1
  • 3.2 - Øvelse 2
• 4 Referanser

Basens egenskaper

1- En base B er det minste mulig sett med vektorer som genererer vektorområdet V.

2- Elementene i B de er lineært uavhengige.

3- Enhver base B av et vektorrom V, tillater å uttrykke alle vektorer av V som en lineær kombinasjon av den, og denne formen er unik for hver vektor. Derfor til B det er også kjent som generator system.

4- Det samme vektorområdet V kan ha forskjellige baser.

Eksempler på baser

Her er flere eksempler på ortonormale baser og baser generelt:

Det kanoniske grunnlaget i ℜ ⁿ

Også kalt naturlig base eller standard base av ℜ ⁿ, hvor ℜ ⁿ er rommet n-dimensjonal, for eksempel er det tredimensjonale rommet ℜ ³. Til verdien av n Det kalles dimensjon av vektorområdet og er betegnet som dim (V).

Alle vektorer som tilhører ℜ ⁿ er representert av n-adas bestilt. For plass ℜⁿ, det kanoniske grunnlaget er:

og₁ = <1,0,… ,0>; og_to = <0,1,… ,0>; ... og_n = <0,0,… ,1>

I dette eksemplet har vi brukt betegnelsen med parentes eller "parentes" og fet skrift for enhetsvektorene og₁, og_to, og₃...

Det kanoniske grunnlaget i ℜ³

De kjente vektorene Jeg, j Y k innrømme den samme representasjonen, og alle tre av dem er nok til å representere vektorene i ℜ ³:

Jeg = <1,0,0 >; j = <0,1,0 >;  k = <0,0,1 >

Det betyr at basen kan uttrykkes slik:

B = <1,0,0 >; <0,1,0 >;  <0,0,1 >

For å verifisere at de er lineært uavhengige, er determinanten dannet med dem ikke-null og også lik 1:

Det skal også være mulig å skrive hvilken som helst vektor som tilhører ℜ ³ som en lineær kombinasjon av dem. For eksempel en kraft hvis rektangulære komponenter er F_x = 4 N, F_Y = -7 N og F._z= 0 N ville bli skrevet i vektorform slik:

F = <4,-7,0 > N = 4Jeg -7j + 0k N.

Derfor Jeg, j Y k utgjøre et generatorsystem på ℜ ³.

Andre ortonormale baser i ℜ³

Standardbasen beskrevet i forrige avsnitt er ikke den eneste ortonormale basen i ℜ³. Her har vi for eksempel basene:

B₁ = ; <- sen θ, cos θ,0 >;  <0,0,1 >

B_to = <3/5, 4/5,0 >; <- 4/5, 3/5,0 >;  <0,0,1 >

Det kan vises at disse basene er ortonormale, for dette husker vi betingelsene som må oppfylles:

-Vektorene som danner basen, må være ortogonale mot hverandre.

-Hver av dem må være enhetlige.

Vi kan bekrefte at vi vet at determinanten som dannes av dem, må være ikke-null og lik 1.

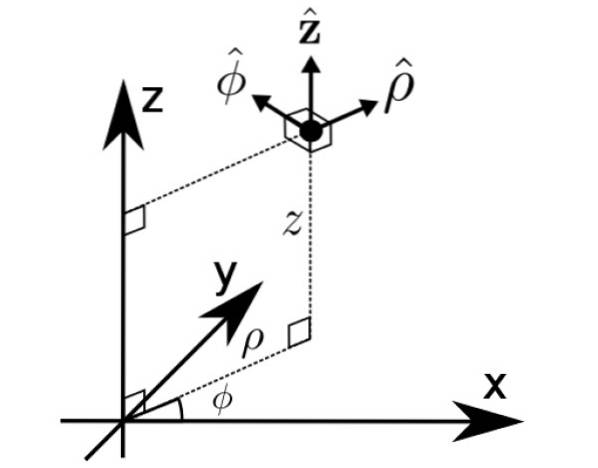
Base B₁ det er nettopp det av sylindriske koordinater ρ, φ og z, en annen måte å uttrykke vektorer i rommet.

Løst øvelser

- Øvelse 1

Vis at basen B = <3/5, 4/5,0 >; <- 4/5, 3/5,0 >;  <0,0,1 > er ortonormal.

Løsning

For å vise at vektorene er vinkelrette på hverandre, vil vi bruke skalarproduktet, også kalt det indre eller punktproduktet til to vektorer.

La være to vektorer eller Y v, dot-produktet er definert av:

eller • v = u.v. cosθ

For å skille vektorene til modulene deres, bruker vi fet skrift for de første og normale bokstaver for de andre. θ er vinkelen mellom eller Y v, Derfor, hvis de er vinkelrette, betyr det at θ = 90º og det skalære produktet er null.

Alternativt, hvis vektorene er gitt med hensyn til komponentene: eller = x, eller_Y,eller_z > og v = x, v_Y,v_z >, prikkproduktet til begge deler, som er kommutativt, beregnes som følger:

eller • v = eller_x .v_x + eller_Y .v_Y + eller_z .v_z

På denne måten er skalarproduktene mellom hvert vektorpar:

Jeg) <3/5, 4/5,0 > • <- 4/5, 3/5,0 > = (3/5). (- 4/5) + (4/5). ((3/5) + 0,0 = (-12/25) + (12/25) = 0

ii) <3/5, 4/5,0 > • <0, 0,1 > = 0

iii) <- 4/5, 3/5,0 > • <0, 0,1 > = 0

For den andre tilstanden beregnes modulen til hver vektor, som oppnås ved:

│u │ = √ (u_x^to + eller_Y^to + eller_z^to)

Dermed er modulene til hver vektor:

│<3/5, 4/5,0 >│ = √ [(3/5)^to + (4/5)^to  + 0^to)] = √ [(9/25) + (16/25)] = √ (25/25) = 1

│<-4/5, 3/5,0 >│ = √ [(-4/5)^to + (3/5)^to  + 0^to)] = √ [(16/25) + (9/25)] = √ (25/25) = 1

│<0, 0,1 >│ = √ [0^to + 0^to  + 1^to)] = 1

Derfor er alle tre enhetsvektorer. Til slutt er determinanten de danner ikke null og lik 1:

- Øvelse 2

Skriv koordinatene til vektoren w = <2, 3,1 > når det gjelder den gamle basen.

Løsning

For å gjøre dette brukes følgende setning:

La B = v₁, v_to, v₃,... v_n en ortonormal basis i rom V med indre produkt, vektoren w er representert av B som følger:

w = <w•v₁> v₁ + <w•v_to> v_to +<w•v₃> v₃ +... <w•v_n> v_n

Dette betyr at vi kan skrive vektoren i base B ved å bruke koeffisientene <w•v₁>, <w•v_to>, ...  <w•v_n>, som de angitte skalarproduktene må beregnes for:

<2, 3,1 > • <3/5, 4/5,0 > = (2). (3/5) + (3). (4/5) + 1.0 = (6/5) + (12/5) = 18/5

<2, 3,1 > • <- 4/5, 3/5,0 > = (2). (- 4/5) + (3). (3/5) + 1.0 = (-8/5) + (9/5) = 1/5

<2, 3,1 > • <0,0,1> = 1

Med oppnådde skalarprodukter blir det bygget en matrise, kalt koordinatmatrise av w.

Derfor koordinatene til vektoren w i base B uttrykkes de av:

[w]_B= [(5/18); (1/5); 1]

Koordinatmatrisen er ikke vektoren, siden en vektor Det er ikke det samme som koordinatene. Dette er bare et sett med tall som tjener til å uttrykke vektoren i en gitt base, ikke vektoren som sådan. De er også avhengig av valgt base.

Til slutt, etter teoremet, vektoren w ville bli uttrykt slik:

w = (18/5) v₁ + (1/5) v_to + v₃

Med: v₁ = <3/5, 4/5,0 >; v_to = <- 4/5, 3/5,0 >; v₃ =  <0,0,1 >, det vil si vektorene til grunnlaget B.

Referanser

1. Larson, R. Fundamenter for lineær algebra. Sjette. Utgave. Cengage læring.
2. Larson, R. 2006. Calculus. 7. Utgave. Volum 2. McGraw Hill.
3. Salas, J. Lineær algebra. Enhet 10. Ortonnormale baser. Gjenopprettet fra: ocw.uc3m.es.
4. Sevilla universitet. Sylindriske koordinater. Vector base. Gjenopprettet fra: laplace.us.es.
5. Wikipedia. Ortonnormal base. Gjenopprettet fra: es.wikipedia.org.