
Tyngdepunktegenskaper, beregning, eksempler
De tyngdepunktet av en kropp av målbar størrelse er det punktet hvor vekten anses å bli brukt. Det er derfor et av de grunnleggende begrepene i Statics.
Den første tilnærmingen i problemene med elementær fysikk består i å anta at ethvert objekt oppfører seg som en punktmasse, det vil si at det ikke har noen dimensjoner og at all massen er konsentrert i et enkelt punkt. Dette gjelder for en boks, en bil, en planet eller en subatomær partikkel. Denne modellen er kjent som partikkelmodell.

Dette er selvfølgelig en tilnærming, som fungerer veldig bra for mange applikasjoner. Det er ikke en lett oppgave å ta hensyn til den individuelle oppførselen til tusenvis og millioner av partikler som ethvert objekt kan inneholde.
Imidlertid må de virkelige dimensjonene av ting tas i betraktning hvis man skal oppnå resultater som er nærmere virkeligheten. Siden vi generelt er i nærheten av jorden, er den stadig tilstedeværende kraften på ethvert legeme nøyaktig vekten.
Artikkelindeks
- 1 Hensyn for å finne tyngdepunktet
- 2 Hvordan beregnes tyngdepunktet?
- 3 eiendommer
- 3.1 -Finne tyngdepunktet til et legeme i statisk likevekt
- 3.2 -Løst eksempel
- 4 Forskjell fra massesenter
- 5 Eksempler på tyngdepunkt
- 5.1 Tyngdepunkt for uregelmessige gjenstander
- 5.2 Balansere objekter
- 6 Referanser
Hensyn for å finne tyngdepunktet
Hvis det skal tas hensyn til kroppsstørrelse, hvor spesifikt skal vekten påføres? Når du har et vilkårlig kontinuerlig objekt, er vekten a distribuert kraft mellom hver av dets bestanddeler.
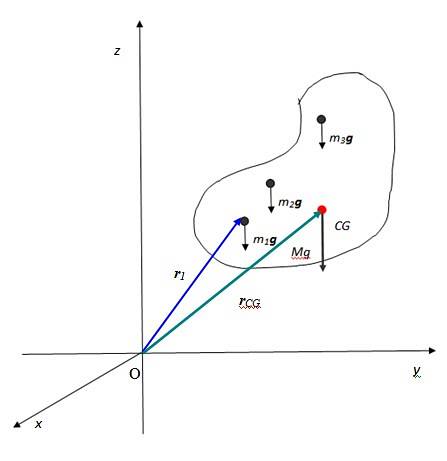
La disse partiklene være m1, mto, m3... Hver og en av dem opplever sin tilsvarende gravitasjonskraft m1g, mtog, m3g ..., alle parallelle. Dette er slik, siden gravitasjonsfeltet på jorden betraktes som konstant i de aller fleste tilfeller, gitt at gjenstandene er små sammenlignet med størrelsen på planeten og ligger nær overflaten..
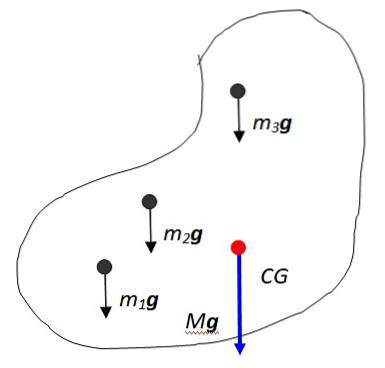
Vektorsummen av disse kreftene resulterer i vekten av objektet, brukt på det punktet som kalles tyngdepunktet i figuren betegnet som CG, som deretter sammenfaller med Massesenter. Massesenteret er igjen punktet der all massen kan betraktes som konsentrert.
Den resulterende vekten har størrelse Mg hvor M er den totale massen til objektet, og selvfølgelig er den rettet vertikalt mot sentrum av jorden. Summasjonsnotasjonen er nyttig for å uttrykke kroppens totale masse:
Tyngdepunktet faller ikke alltid sammen med et materielt punkt. For eksempel er CG av en ring i sitt geometriske sentrum, hvor det ikke er noen masse i seg selv. Likevel, hvis du vil analysere kreftene som virker på en bøyle, må du bruke vekten til dette nøyaktige punktet.
I de tilfeller der objektet har en vilkårlig form, hvis det er homogent, kan massesenteret fortsatt beregnes ved å finne sentroid eller tyngdepunktet til figuren.
Hvordan beregner du tyngdepunktet?
I prinsippet, hvis tyngdepunktet (CG) og massesenteret (cm) faller sammen mens gravitasjonsfeltet er jevnt, kan cm beregnes og vekten påføres.
La oss se på to tilfeller: den første er en der massedistribusjonen er diskret; det vil si at hver masse som utgjør systemet kan telles og tildeles et nummer i, som det ble gjort i forrige eksempel.
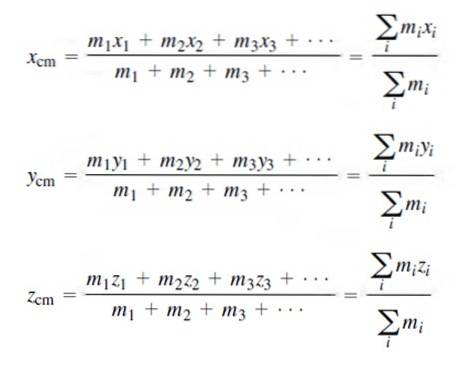
Koordinatene til massesenteret for en diskret massefordeling er:
Naturligvis er summen av alle massene lik den totale massen til systemet M, som angitt ovenfor..
De tre ligningene er redusert til en kompakt form ved å ta i betraktning vektoren rcm eller posisjonsvektor for massesenteret:
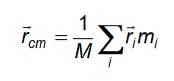
Og i tilfelle en kontinuerlig massefordeling, der partiklene har forskjellig størrelse og ikke kan skilles for å telle dem, erstattes summen av en integral som er laget over volumet okkupert av det aktuelle objektet:
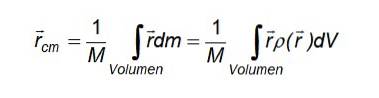
Hvor r er posisjonsvektoren til en differensialmasse dm og definisjonen av massetetthet har blitt brukt for å uttrykke massedifferansen dm inneholdt i en volumdifferensial dV:
Eiendommer
Noen viktige betraktninger om massesenteret er som følger:
- Selv om det kreves et referansesystem for å etablere posisjonene, er ikke massesenteret avhengig av valget av systemet, siden det er en egenskap for objektet.
- Når objektet har en akse eller et symmetriplan, er massesenteret på den aksen eller planet. Hvis du utnytter denne omstendigheten, sparer du beregningstid.
- Alle eksterne krefter som virker på objektet kan påføres massesenteret. Å holde styr på bevegelsen til dette punktet gir en global ide om objektets bevegelse og letter arbeidet med å studere oppførselen..
-Finne tyngdepunktet til et legeme i statisk likevekt
Anta at du vil gjøre kroppen i forrige figur i statisk likevekt, det vil si at den ikke oversettes eller roterer om en vilkårlig rotasjonsakse som kan være O.

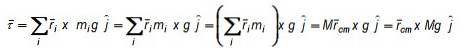
-Arbeidet eksempel
En tynn stang av jevnt materiale er 6 m lang og veier 30 N. En 50 N vekt henges i venstre ende og 20 N vekt henges i høyre ende. Finn: a) Størrelsen på den oppadgående kraften som er nødvendig for å opprettholde likevekten til stangen, b) Tyngdepunktet til settet.
Løsning
Kraftdiagrammet er vist i følgende figur. Vekten av stangen påføres i tyngdepunktet, som sammenfaller med det geometriske sentrum. Den eneste dimensjonen til stangen tatt i betraktning er lengden, siden uttalelsen informerer om at den er tynn.
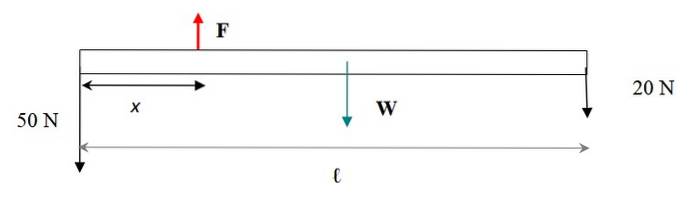
For at bar + vekter systemet skal forbli i translasjonsvekt, må summen av kreftene være null. Kreftene er vertikale, hvis vi vurderer opp med tegn + og ned med tegn - så:
F- 50 - 20 - 30 N = 0
F = 100 N
Denne styrken garanterer translasjonsbalansen. Tar torsjonsmomentene til alle kreftene i forhold til en akse som passerer gjennom den venstre enden av systemet og bruker definisjonen:
t = r x F
Øyeblikkene til alle disse kreftene rundt det valgte punktet er vinkelrett på stolpens plan:
tF = xF = 100x
tW = - (l / 2) mg = -3m. 30 N = -90 N.m
t1 = 0 (siden 50 N-kraften passerer gjennom den valgte rotasjonsaksen og ikke utøver øyeblikk)
tto = -lFto = 6 m. 20 N = -120 N.m
Derfor:
100 x -90 -120 N.m = 0
x = 2,10 m
Tyngdepunktet til stangen + vekter sett er 2.10 meter fra venstre ende av stangen.
Forskjell fra massesenter
Tyngdepunktet faller sammen med massesenteret, som angitt, så lenge jordens gravitasjonsfelt er konstant for at alle punkter i objektet skal tas i betraktning. Jordens gravitasjonsfelt er ikke noe annet enn den velkjente og kjente verdien av g = 9,8 m / sto rettet vertikalt ned.
Selv om verdien på g varierer med bredde og høyde, påvirker disse vanligvis ikke gjenstandene som er mesteparten av tiden. Det ville være veldig annerledes hvis du vurderer en stor kropp i nærheten av jorden, for eksempel en asteroide som er veldig nær planeten.
Asteroiden har sitt eget massesenter, men tyngdepunktet trenger ikke lenger å falle sammen med dette, siden g vil sannsynligvis oppleve store variasjoner i størrelse, gitt størrelsen på asteroiden og at vektene til hver partikkel kanskje ikke er parallelle.
En annen grunnleggende forskjell er at massesenteret blir funnet uansett om det er en kraft som kalles vekt påført objektet eller ikke. Det er en iboende egenskap til objektet som avslører for oss hvordan massen fordeles i forhold til dens geometri.
Massesenteret eksisterer uansett om det er brukt vekt eller ikke. Og den ligger i samme posisjon selv om objektet beveger seg til en annen planet der gravitasjonsfeltet er annerledes..
På den annen side er tyngdepunktet tydelig knyttet til påføring av vekt, som vi har sett gjennom de foregående avsnittene..
Eksempler på tyngdepunkt
Tyngdepunkt for uregelmessige gjenstander
Det er veldig enkelt å finne ut hvor tyngdepunktet til en uregelmessig gjenstand som en kopp er. Først er den suspendert fra hvilket som helst punkt, og derfra trekkes en vertikal linje (i figur 5 er det fuchsia-linjen i det venstre bildet).
Deretter blir den suspendert fra et annet punkt, og en ny vertikal tegnes (turkis linje i høyre bilde). Krysset mellom begge linjene er koppens tyngdepunkt.

Balansere gjenstander
La oss analysere stabiliteten til en lastebil som kjører på veien. Når tyngdepunktet er over bunnen av trucken, vil ikke trucken velte. Bildet til venstre er den mest stabile posisjonen.
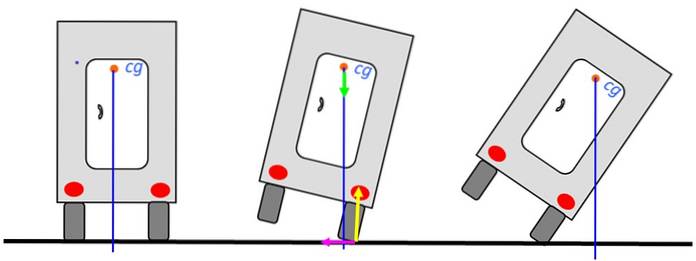
Selv når trucken er vippet mot høyre, vil den være i stand til å gå tilbake til en stabil likevektsposisjon, som på midttegningen, siden loddrett fortsatt går gjennom basen. Men når denne linjen passerer utenfor, vil trucken velte.
Diagrammet viser kreftene ved støttepunktet: normal i gult, vekt i grønt og statisk gni til venstre i fuchsia. Normal og friksjon påføres rotasjonsaksen, slik at de ikke utøver moment. Derfor vil de ikke bidra til å velte lastebilen.
Vekten forblir, som utøver et dreiemoment, heldigvis mot klokken, og som har en tendens til å bringe trucken tilbake i likevektsstilling. Merk at den vertikale linjen passerer gjennom støtteflaten, som er dekket.
Når trucken er i helt høyre posisjon, endres vektens dreiemoment til klokken. Kan ikke imøtegås en annen gang, vil trucken velte.
Referanser
- Bauer, W. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill. 247-253.
- Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. 6.… Ed Prentice Hall. 229-238.
- Resnick, R. (1999). Fysisk. Vol. 1. 3. utgave på spansk. Compañía Editorial Continental S.A. de C.V. 331-341.
- Rex, A. 2011. Fundamentals of Physics. Pearson. 146-155.
- Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 1.340-346.



Ingen har kommentert denne artikkelen ennå.