Hvordan finne vinkelen til en trekant?

Det er flere måter å beregne sidene og vinklene til en trekant. Disse avhenger av hvilken type trekant du jobber med.

I denne muligheten vil det bli vist hvordan man beregner sidene og vinklene til en rett trekant, forutsatt at visse data i trekanten med kjent.

Elementene som skal brukes er:

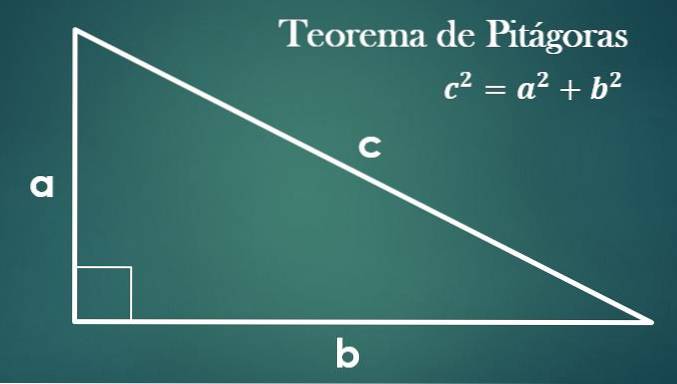
- Pythagoras teorem

Gitt en høyre trekant med bena "a", "b" og hypotenuse "c", er det sant at "c² = a² + b²".

- Område av en trekant

Formelen for å beregne arealet til en hvilken som helst trekant er A = (b × h) / 2, hvor “b” er lengden på basen og “h” er lengden på høyden.

- Vinkler av en trekant

Summen av de tre innvendige vinklene i en trekant er 180º.

- Trigonometriske funksjoner:

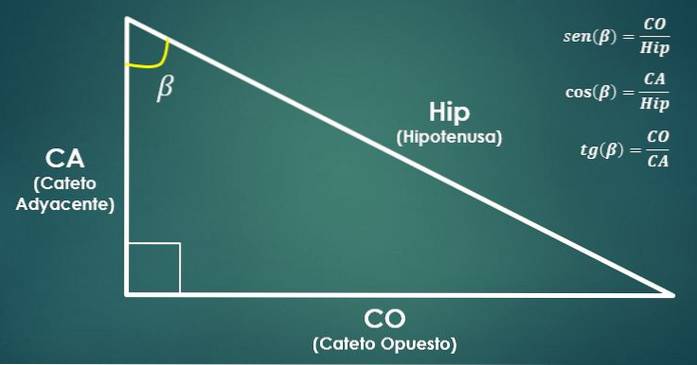
Tenk på en riktig trekant. Deretter defineres de trigonometriske funksjonene sinus, cosinus og tangens til vinkelen beta (β) som følger:

sin (β) = CO / Hip, cos (β) = CA / Hip og tan (β) = CO / CA.

Hvordan finne sidene og vinklene til en rett trekant?

Gitt en rett trekant ABC, kan følgende situasjoner oppstå:

1- De to bena er kjent

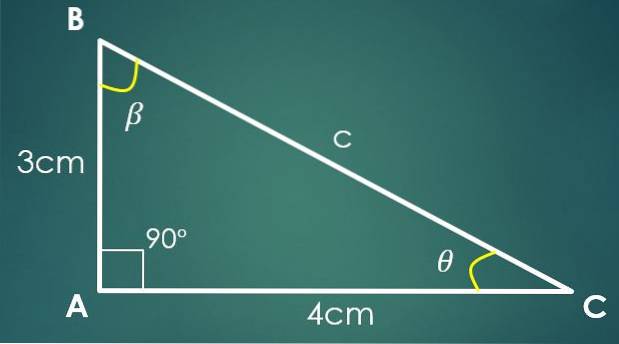
Hvis etappe “a” måler 3 cm og etappe “b” måler 4 cm, brukes den pythagoriske teoremet til å beregne verdien av “c”. Ved å erstatte verdiene til "a" og "b" oppnår vi at c² = 25 cm², noe som betyr at c = 5 cm.

Nå, hvis vinkelen β er motsatt benet "b", så er sin (β) = 4/5. Ved å bruke sinusens omvendte funksjon, oppnår vi i denne siste likheten at β = 53,13º. To indre vinkler i trekanten er allerede kjent.

La θ være vinkelen som gjenstår å være kjent, så 90º + 53,13º + θ = 180º, hvorfra vi oppnår at θ = 36,87º.

I dette tilfellet er det ikke nødvendig at de kjente sidene er de to benene, det viktigste er å vite verdien av to sider..

2- Et bein er kjent og området

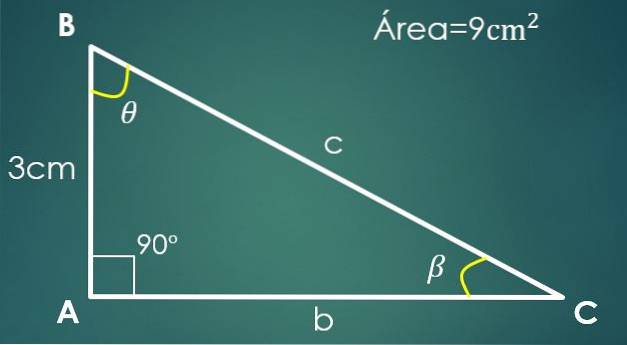
La a = 3 cm være det kjente benet og A = 9 cm² arealet av trekanten.

I en rett trekant kan det ene benet betraktes som basen og det andre som høyden (siden de er vinkelrette).

Anta at “a” er basen, derfor er 9 = (3 × h) / 2, hvorfra vi får ut at det andre benet er 6 cm. For å beregne hypotenusen, fortsett som i forrige tilfelle, og vi får at c = √45 cm.

Nå, hvis vinkelen β er motsatt benet “a”, så er sin (β) = 3 / √45. Løsning for β oppnås at verdien er 26,57º. Vi trenger bare å vite verdien av den tredje vinkelen θ.

Det er tilfreds at 90º + 26,57º + θ = 180º, hvorfra det konkluderes med at θ = 63,43º.

3- En vinkel og et ben er kjent

La β = 45º være den kjente vinkelen og a = 3 cm den kjente etappen, der benet "a" er motsatt vinkel β. Ved hjelp av tangensformelen får vi at tg (45º) = 3 / CA, hvorfra det følger at CA = 3 cm.

Ved bruk av Pythagoras teorem oppnås det at c² = 18 cm², det vil si c = 3√2 cm.

Det er kjent at en vinkel måler 90º og at β måler 45º, herfra konkluderes det at den tredje vinkelen måler 45º.

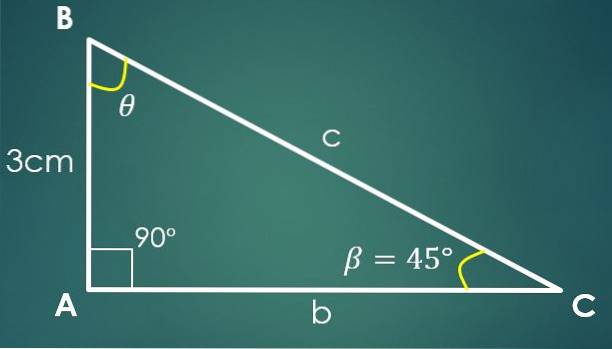
I dette tilfellet trenger ikke den kjente siden å være et ben, det kan være hvilken som helst av de tre sidene av trekanten.

Referanser

1. Landaverde, F. d. (1997). Geometri (Omtrykk red.). Framgang.
2. Leake, D. (2006). Trekanter (illustrert utg.). Heinemann-Raintree.
3. Pérez, C. D. (2006). Forberegning. Pearson Education.
4. Ruiz, Á., & Barrantes, H. (2006). Geometrier. CR-teknologi.
5. Sullivan, M. (1997). Forberegning. Pearson Education.
6. Sullivan, M. (1997). Trigonometri og analytisk geometri. Pearson Education.