
Jevnhetsforholdskonsept, applikasjoner og eksempler
De likevektsforhold De er nødvendige for at kroppen skal forbli i ro eller i ensartet rettlinjet bevegelse. I det første tilfellet sies det at objektet er i statisk likevekt, mens det andre er i dynamisk likevekt.
Forutsatt at den bevegelige gjenstanden er en partikkel, i hvilket tilfelle dimensjonene ikke tas i betraktning, er det nok at summen av krefter som virker på den annulleres..

Men et stort flertall av bevegelige objekter har merkbare dimensjoner, derfor er denne tilstanden ikke nok til å garantere likevekt, som uansett er fravær av akselerasjon, ikke bevegelse..
Artikkelindeks
- 1 Første og andre likevektstilstand
- 2 Søknader
- 2.1 Isostatisk likevekt
- 2.2 Hvordan fusjon fungerer i kjernen
- 2.3 Konstruksjon
- 3 Typer statisk likevekt
- 3.1 Stabil likevekt
- 3.2 Likegyldig eller nøytral balanse
- 3.3 Ustabil likevekt
- 4 Eksempel: partikkelstatistikk
- 5 Øvelse løst
- 5.1 Løsning
- 6 Interessante emner
- 7 Referanser
Første og andre likevektstilstand
La oss se: hvis summen av krefter er null, er det sant at objektet ikke kommer til å bevege seg eller bevege seg med en akselerert hastighet, men det kan fortsatt begynne å rotere.
Derfor, for å unngå rotasjoner, må en annen betingelse legges til: at summen av dreiemomentene eller vridningsmomentene forårsaket av eksterne krefter som virker på det, rundt et hvilket som helst punkt, også annulleres..
Kort sagt, betegner som F nettokraftvektoren y τ eller M til nettomomentvektoren vil vi ha:
Første likevektstilstand
∑ F = 0
Noe som betyr at: ∑ Fx = 0, ∑ FY = 0 og ∑ Fz = 0
Andre likevektstilstand
∑ τ = 0 eller ∑ M = 0
Med dreiemomentene eller øyeblikkene beregnet til hvilket som helst punkt.
I det følgende vil vi anta at den bevegelige gjenstanden er en stiv kropp, en som ikke gjennomgår noen deformasjon..
applikasjoner
Til tross for at bevegelse ser ut til å være fellesnevner i universet, er balanse også til stede i mange aspekter av naturen og i objektene som omgir oss..
Isostatisk likevekt
På planetarisk skala er Jorden inne isostatisk likevekt, en slags gravitasjonsbalanse av jordskorpen, hvis tetthet ikke er jevn.
Forskjellene i tettheten til de forskjellige blokkene eller områdene av jordskorpen kompenseres av høydeforskjellene som kjennetegner planetens orografi. Det fungerer på samme måte som forskjellige materialer er mer eller mindre nedsenket i vann i henhold til dens tetthet og når likevekt.
Men siden skorpeblokkene ikke flyter ordentlig i vann, men i kappen, som er mye mer tyktflytende, kalles ikke likevekten hydrostatisk, men isostatisk..
Hvordan fusjon fungerer i kjernen
I stjerner som solen vår, holder balansen mellom tyngdekraften som komprimerer dem og det hydrostatiske trykket som utvider dem, fusjonsreaktoren i kjernen til stjernen, som holder den i live. Vi er avhengige av denne balansen for at Jorden skal motta nødvendig lys og varme.
Bygning
I lokal skala ønsker vi at bygninger og konstruksjoner skal være stabile, det vil si å adlyde likevektsforhold, særlig statisk likevekt..
Derfor oppstod statikk, som er grenen av mekanikk dedikert til å studere kroppsbalansen og alt som trengs for å holde dem på den måten..
Typer av statisk likevekt
I praksis finner vi at statisk likevekt kan være av tre slag:
Stabil likevekt
Det oppstår når objektet beveger seg fra sin posisjon og umiddelbart kommer tilbake til det når kraften som dyttet det bort opphører. Jo nærmere et objekt er bakken, desto mer sannsynlig er det å være i stabil likevekt.
Kulen til høyre i figur 2 er et godt eksempel, hvis vi fjerner den fra likevektsposisjonen i bunnen av bollen, vil tyngdekraften ta vare på den raske retur.
Likegyldig eller nøytral balanse
Det skjer når objektet, til tross for at det blir flyttet, fremdeles er i balanse. Runde gjenstander som kulen, når de plasseres på flate overflater, er i likegyldig likevekt.
Ustabil balanse
Det oppstår når objektet beveger seg fra likevektsposisjon, det ikke kommer tilbake til det. Hvis vi flytter ballen bort fra toppen av bakken til venstre, er det sikkert at den ikke kommer tilbake under egen kraft..

Eksempel: partikkelstatistikk
Anta en masseblokk m på et skrånende plan, der all masse antas å være konsentrert i sitt geometriske sentrum.
Den horisontale komponenten av vekten Wx den har en tendens til å få blokken til å gli nedover, derfor er det behov for en annen motstridende kraft. Hvis vi vil at blokken skal være i ro, er denne kraften den statiske friksjonen. Men hvis vi lar blokken gli nedoverbakke med konstant hastighet, så er kraften som kreves dynamisk friksjon..
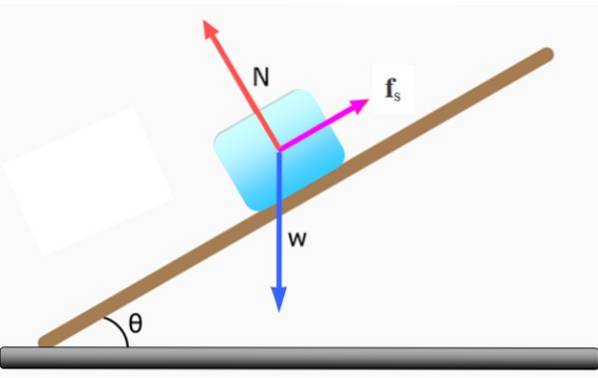
I mangel av friksjon vil blokken gli raskt nedover, og i dette tilfellet vil det ikke være noen likevekt.
For at blokken skal være i ro, kreftene som virker på den: vekt W, det normale N og den statiske friksjonen Fs, de må kompenseres. Deretter:
∑ FY = 0 → N - WY = 0
∑ Fx = 0 → Wx - Fs = 0
Statisk friksjon balanserer den horisontale delen av vekten: Wx = fs og derfor:
Fs = m. g .sen θ
Treningen løst
Et 21,5 kg trafikklys henger fra en homogen aluminiumsstang AB med en vekt på 12 kg og 7,5 m, støttet av en horisontal tau-CD, som vist på figuren. Finne:
a) DC-kabelspenningen
b) De horisontale og vertikale komponentene til kraften som utøves av sving A på stolpen.
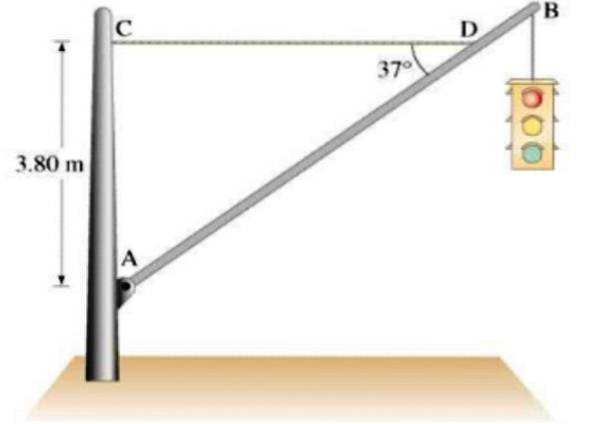
Løsning
Diagrammet over krefter som påføres stangen er konstruert, med vekten W, spenningene i akkordene og de horisontale og vertikale komponentene i svingreaksjonen, kalt Rx og RY. Da gjelder likevektsforhold.
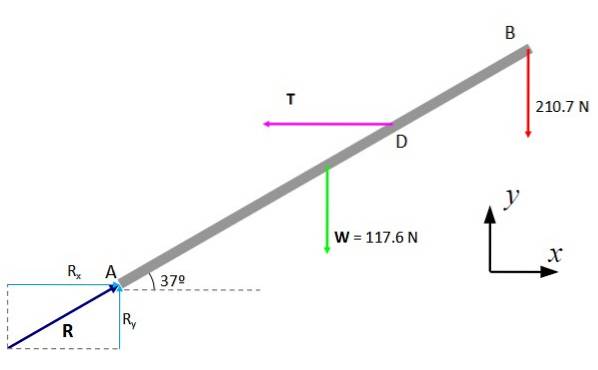
Første tilstand
Å være et problem i planet, tilbyr den første likevektstilstanden to ligninger:
ΣFx = 0
ΣFY = 0
Fra den første:
Rx - T = 0
Rx = T
Og det andre:
RY - 117,6 N - 210,7 N = 0
RY = 328,3 N
Den horisontale komponenten i reaksjonen er lik størrelsen på spenningen T.
Andre tilstand
Punkt A i figur 5 er valgt som rotasjonssenter, på denne måten reaksjonsarmen R er null, husk at øyeblikkets størrelse er gitt av:
M = F┴ d
Hvor F┴ er den vinkelrette komponenten av kraften og d er avstanden mellom rotasjonsaksen og kraftens påføringspunkt. Vi får en ligning:
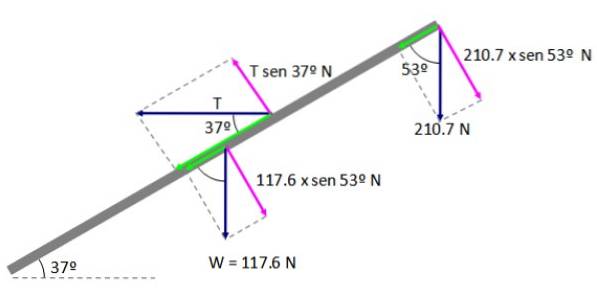
ΣMTIL = 0
(210,7 × sin 53º) AB + (117,6 × sin 53º) (AB / 2) - (T × sin 37º) AD = 0
Avstanden AD er:
AD = (3,8 m / sin 37º) = 6,3 m
(210,7 × sin 53º N) (7,5 m) + (117,6 × sin 53º N) (3,75 m) - (T × sin 37º N) (6,3 m) = 0
Gjennomføre de angitte operasjonene:
1262.04 + 352.20 - 3.8T = 0
Å løse for T får vi:
T = 424,8 N
Fra den første tilstanden, Rx = T, derfor:
Rx = 424,8 N
Temaer av interesse
Første likevektstilstand.
Andre likevektstilstand.
Referanser
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
- Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volum 4. Partikkelsystemer. Redigert av Douglas Figueroa (USB).
- Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. Sjette. Ed prentice hall.
- Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 1.
- Wikipedia. Isostasia. Gjenopprettet fra: es.wikipedia.org.


Ingen har kommentert denne artikkelen ennå.