
Konduktansformler, beregning, eksempler, øvelser
De konduktans av en leder er definert som anlegget den har for å passere den elektriske strømmen. Det avhenger ikke bare av materialet som brukes til fremstilling, men også av geometrien: lengde og tverrsnittsareal.
Symbolet som brukes for ledningsevne er G, og det er det motsatte av elektrisk motstand R, en litt mer kjent størrelse. SI International System-enheten for konduktans er omvendt av ohm, betegnet som Ω-1 og mottar navnet på siemens (S).

Andre termer som brukes i elektrisitet som høres ut som konduktans og er beslektede er ledningsevne og kjøring, men de skal ikke forveksles. Den første av disse begrepene er en iboende egenskap av stoffet som lederen er laget med, og den andre beskriver strømmen av elektrisk ladning gjennom den..
For en elektrisk leder med konstant tverrsnittsareal TIL, lengde L og ledningsevne σ, konduktansen er gitt av:
G = σ.A / L
Jo høyere konduktivitet, jo høyere konduktans. Jo større tverrsnittsarealet er, desto lettere er det for lederen å passere strøm. Tvert imot, jo større lengde L er, desto lavere konduktans, siden de nåværende bærerne mister mer energi på lengre stier..
Artikkelindeks
- 1 Hvordan beregnes konduktans?
- 1.1 Ledningsenheter
- 2 Eksempler
- 2.1 Konduktivitet og konduktans
- 2.2 Motstander parallelt
- 3 Øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 4 Referanser
Hvordan beregnes konduktans?
Konduktansen G for en leder med konstant tverrsnittsareal beregnes i henhold til ligningen gitt ovenfor. Dette er viktig, for hvis tverrsnittet ikke er konstant, må du bruke den integrerte kalkulatoren for å finne både motstand og konduktans.
Siden det er det motsatte av motstanden, kan konduktansen G beregnes og vite at:
G = 1 / R
Faktisk kan den elektriske motstanden til en leder måles direkte med et multimeter, en enhet som også måler strøm og spenning..
Ledningsenheter
Som nevnt i begynnelsen er ledningsenheten i det internasjonale systemet Siemens (S). En leder sies å ha en konduktans på 1 S hvis strømmen gjennom den øker med 1 ampere for hver volt potensialforskjell..
La oss se hvordan det er mulig gjennom Ohms lov, hvis det er skrevet i form av konduktans:
V = I.R = I / G
Hvor V er spenningen eller potensialforskjellen mellom endene på lederen e Jeg nåværende intensitet. Når det gjelder disse størrelsene, ser formelen slik ut:
G = I / V
Tidligere var enheten for konduktans den mho (ohm skrevet bakover) betegnet som Ʊ, som er en omvendt hovedstad omega. Denne notasjonen ble utfaset og ble erstattet av siemens til ære for den tyske ingeniøren og oppfinneren Ernst Von Siemens (1816-1892), pioner innen telekommunikasjon, men begge er helt like.
1 mho = 1 siemens = 1 A / V (ampere / volt)
I andre målesystemer statsiemens (statS) (i cgs eller centimeter-gram-sekundersystemet) og absiemens (abS) (elektromagnetisk cgs-system) med "s" på slutten, uten å indikere entall eller flertall, siden de kommer fra et riktig navn.
Noen ekvivalenser
1 statS = 1.11265 x 10 -12 siemens
1 abS = 1 x 109 siemens
Eksempler
Som nevnt tidligere, med ledende motstand, er konduktansen umiddelbart kjent når man bestemmer den inverse eller gjensidige verdien. På denne måten tilsvarer en elektrisk motstand på 100 ohm for eksempel 0,01 siemen.
Her er to eksempler på bruk av konduktans:
Konduktivitet og konduktans
De er forskjellige begreper, som allerede angitt. Ledningsevne er en egenskap for stoffet som lederen er laget med, mens ledning er riktig for lederen.
Ledningsevne kan uttrykkes i form av G som:
σ = G. (L / A)
Her er en tabell med ledningsevnen til ofte brukte ledende materialer:
Tabell 1. Ledningsevner, resistiviteter og termisk koeffisient for noen ledere. Referansetemperatur: 20 ºC.
| Metall | σ x 106 (Dere) | ρ x 10-8 (Ω.m) | α ºC-1 |
|---|---|---|---|
| Sølv | 62.9 | 1,59 | 0,0058 |
| Kobber | 56.5 | 1,77 | 0,0038 |
| Gull | 41.0 | 2.44 | 0,0034 |
| Aluminium | 35.4 | 2.82 | 0,0039 |
| Wolfram | 18.0 | 5.60 | 0,0045 |
| Jern | 10.0 | 10.0 | 0,0050 |
Motstander parallelt
Når du har kretser med motstander parallelt, er det noen ganger nødvendig å oppnå tilsvarende motstand. Å vite verdien av den tilsvarende motstanden gjør det mulig å erstatte en enkelt verdi for settet med motstander.
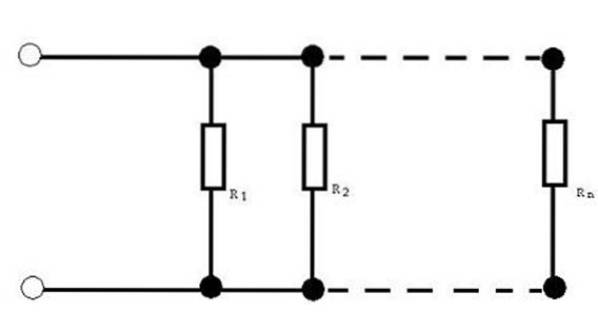
For denne motstandskonfigurasjonen er ekvivalent motstand gitt av:
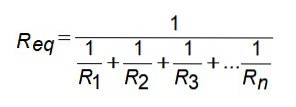
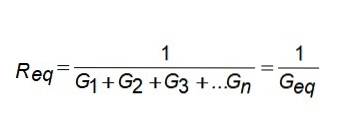
Gekv = G1 + Gto + G3 +... Gn
Det vil si at den tilsvarende konduktansen er summen av konduktansene. Hvis du vil vite tilsvarende motstand, snur du bare resultatet.
Opplæring
- Øvelse 1
a) Skriv Ohms lov når det gjelder konduktans.
b) Finn konduktansen til en wolframtråd 5,4 cm lang og 0,15 mm i diameter.
c) Nå føres en strøm på 1,5 A gjennom ledningen. Hva er den potensielle forskjellen mellom endene på denne lederen?
Løsning til
Fra de foregående avsnittene må du:
V = I / G
G = σ.A / L
Ved å erstatte sistnevnte i det første ser det slik ut:
V = I /(σ.A/L) = I.L / σ.A
Hvor:
-Jeg er intensiteten til strømmen.
-L er lengden på lederen.
-σ er ledningsevnen.
-A er tverrsnittsområdet.
Løsning b
For å beregne konduktansen til denne wolframtråden, kreves dens ledningsevne, som finnes i tabell 1:
σ = 18 x 106 Dere
L = 5,4 cm = 5,4 x 10-to m
D = 0. 15 mm = 0,15 x 10-3 m
A = π.Dto / 4 = π. (0,15 x 10-3 m)to / 4 = 1,77 x 10-8 mto
Å erstatte i ligningen vi har:
G = σ.A / L = 18 x 106 Dere. 1,77 x 10-8 mto / 0,15 x 10-3 m = 2120,6 S.
Løsning c
V = I / G = 1,5 A / 2120,6 S = 0,71 mV.
- Øvelse 2
Finn ekvivalent motstand i følgende krets og vite at jegeller = 2 A, beregne ix og kraften som ledes av kretsen:
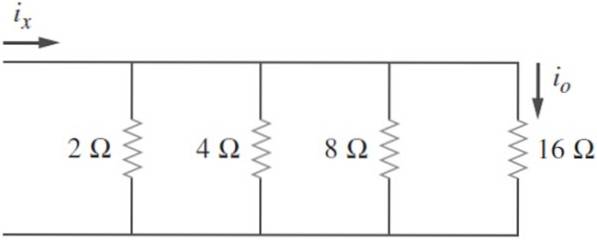
Løsning
Motstander er oppført: R1= 2 Ω; Rto= 4 Ω; R3= 8 Ω; R4= 16 Ω
Deretter beregnes konduktansen i hvert tilfelle: G1 = 0,5 Ʊ; Gto = 0,25 Ʊ; G3 = 0,125 Ʊ; G4 = 0,0625 Ʊ
Og til slutt blir de lagt til som angitt før, for å finne tilsvarende ledningsevne:
Gekv = G1 + Gto + G3 +... Gn = 0,5 Ʊ + 0,25 Ʊ + 0,125 Ʊ + 0,0625 Ʊ = 0,9375 Ʊ
Derfor Rekv = 1,07 Ω.
Spenningen over R4 er V4 = ieller. R4 = 2 A. 16 Ω = 32 V, og det er det samme for alle motstander, siden de er koblet parallelt. Da er det mulig å finne strømmen som strømmer gjennom hver motstand:
-Jeg1 = V1 / R1 = 32 V / 2 Ω = 16 A.
-Jegto = Vto / Rto = 32 V / 4 Ω = 8 A.
-Jeg3 = V3 / R3 = 32 V / 8 Ω = 4 A.
-Jegx = i1 + Jegto + Jeg3 + Jegeller = 16 + 8 + 4 + 2 A = 30 A.
Til slutt er den spredte kraften P:
P = (ix)to. Rekv = 30 A x 1,07 Ω = 32,1 W
Referanser
- Alexander, C. 2006. Grunnleggende om elektriske kretser. 3.. Utgave. Mcgraw hill.
- Konvertering megaampere / millivolt til absiemens kalkulator. Gjenopprettet fra: pinkbird.org.
- García, L. 2014. Elektromagnetisme. 2. plass. Utgave. Industrial University of Santander. Colombia.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Roller, D. 1990. Fysikk. Elektrisitet, magnetisme og optikk. Volum II. Redaksjonell Reverté.
- Wikipedia. Elektrisk ledning. Gjenopprettet fra: es.wikipedia.org.
- Wikipedia. Siemens. Gjenopprettet fra: es.wikipedia.org.



Ingen har kommentert denne artikkelen ennå.