De konstant av proporsjonalitet Det er et relasjonelt numerisk element, som brukes til å definere likhetsmønsteret mellom to størrelser som endres samtidig. Det er veldig vanlig å representere det som en lineær funksjon på en generisk måte ved å bruke uttrykket F (X) = k.X. Dette er imidlertid ikke den eneste representasjonen av en mulig proporsjonalitet.
For eksempel har forholdet mellom X og Y i funksjonen Y = 3x en konstant proporsjonalitet lik 3. Det observeres at når den uavhengige variabelen X vokser, vil også den avhengige variabelen Y, tredoble verdien forrige.
Endringene som brukes på den ene variabelen har umiddelbare konsekvenser for den andre, slik at det er en verdi kjent som proporsjonalitetskonstanten. Dette tjener til å relatere de forskjellige størrelsene som begge variablene får.
Artikkelindeks
I henhold til trenden i endringen av variablene kan proporsjonalitetene klassifiseres i to typer.
Foreslår et enveis forhold mellom to størrelser. I den, hvis den uavhengige variabelen viser noe vekst, vil den avhengige variabelen også vokse. Tilsvarende vil enhver reduksjon i den uavhengige variabelen forårsake en reduksjon i størrelsen på Y.
For eksempel den lineære funksjonen som ble brukt i innledningen; Y = 3X, tilsvarer et direkte forhold til proporsjonalitet. Dette er fordi økningen i den uavhengige variabelen X vil forårsake en tredobling av den forrige verdien tatt av den avhengige variabelen Y.
Tilsvarende vil den avhengige variabelen reduseres tre ganger sin verdi når X synker i størrelse.
Verdien av proporsjonalitetskonstanten "K" i et direkte forhold er definert som K = Y / X.
I denne typen funksjoner presenteres forholdet mellom variablene antonymt, hvor vekst eller reduksjon av den uavhengige variabelen tilsvarer henholdsvis reduksjon eller vekst av den avhengige variabelen..
For eksempel er funksjonen F (x) = k / x et omvendt eller indirekte forhold. Siden verdien av den uavhengige variabelen begynner å øke, vil verdien av k bli delt med et økende antall, noe som får den avhengige variabelen til å synke i verdi i forhold til andelen.
Avhengig av verdien tatt av K, kan trenden til den inverse proporsjonale funksjonen defineres. Hvis k> 0, vil funksjonen avta på alle reelle tall. Og grafen vil være i 1. og 3. kvadrant.
Tvert imot, hvis verdien av K er negativ eller mindre enn null, vil funksjonen øke, og grafen vil bli funnet i 2. og 4. kvadrant.
Det er forskjellige sammenhenger der definisjonen av proporsjonalitetskonstanten kan være nødvendig. I de forskjellige tilfellene vil forskjellige data om problemet vises, hvor studiet av disse endelig vil gi verdien av K.
På en generisk måte kan ovennevnte oppsummeres. Verdiene til K tilsvarer to uttrykk avhengig av typen proporsjonalitet som er tilstede:
- Direkte: K = Y / X
- Invers eller indirekte: K = Y.X
Noen ganger vil grafen til en funksjon bare være delvis eller fullstendig kjent. I disse tilfellene vil det være nødvendig med grafisk analyse å bestemme typen proporsjonalitet. Da vil det være nødvendig å definere en koordinat som gjør det mulig å verifisere verdiene til X og Y som skal gjelde for den tilsvarende formelen til K.
Grafene som refererer til direkte proporsjonaliteter er lineære. På den annen side tar grafene over inverse proporsjonale funksjoner vanligvis form av hyperboler.
I noen tilfeller er det en verditabell med verdiene som tilsvarer hver iterasjon av den uavhengige variabelen. Normalt innebærer dette realiseringen av grafen i tillegg til å definere verdien av K.
Returnerer uttrykket som definerer funksjonen analytisk. Verdien av K kan løses direkte, eller den kan også utledes fra selve uttrykket.
I andre treningsmodeller presenteres visse data, som refererer til forholdet mellom verdiene. Dette gjør det nødvendig å bruke den direkte eller sammensatte regelen på tre for å definere andre nødvendige data i øvelsen..
Begrepet proporsjonalitet har alltid eksistert. Ikke bare i tankene og arbeidet til de store matematikerne, men i befolkningens hverdag på grunn av dets praktiske og anvendelige.
Det er veldig vanlig å finne situasjoner som krever en forholdsmessig tilnærming. Disse presenteres i hvert tilfelle der det er nødvendig å sammenligne variabler og fenomener som har visse sammenhenger.
Gjennom en tidslinje kan vi karakterisere de historiske øyeblikkene der matematiske fremskritt angående proporsjonalitet er blitt brukt..
- 2. århundre f.Kr. Brøkdel og andel lagringssystem er vedtatt i Hellas.
- 5. århundre f.Kr. Andelen som relaterer siden og diagonalen til et firkant, blir også oppdaget i Hellas.
- 600 f.Kr. Thales of Miletus presenterer sin teorem om proporsjonalitet.
- År 900. Desimalsystemet som tidligere ble brukt av India, utvides i forholdstall og proporsjoner. Bidrag fra araberne.
- XVII århundre. Bidrag angående proporsjoner kommer i Eulers beregning.
- XIX århundre. Gauss bidrar med begrepet kompleks antall og proporsjon.
- Tjuende århundre. Proportionalitet som funksjonsmodell er definert av Azcarate og Deulofeo.
Det kreves å beregne verdien av variablene x, y, z og g. Å vite følgende proporsjonale forhold:
3x + 2y - 6z + 8g = 1925
x / 3 = y / 8 = z / 3 = g / 5
Vi fortsetter med å definere de relative verdiene til proporsjonalitetskonstanten. Disse kan fås fra den andre relasjonen, hvor verdien som deler hver variabel indikerer en relasjon eller et forhold som refererer til K.
X = 3k y = 2k z = 3k g = 5k
Verdiene erstattes i det første uttrykket, der det nye systemet vil bli evaluert i en enkelt variabel k.
3 (3k) + 2 (2k) - 6 (3k) + 8 (5k) = 1925
9k + 4k -18k + 40k = 1925
35k = 1925
K = 1925/35 = 55
Ved å bruke denne verdien av proporsjonalitetskonstanten kan vi finne figuren som definerer hver av variablene.
x = 3 (55) = 165 y = 2 (55) = 110
z = 3 (55) = 165 g = 5 (55) = 275
Beregn proporsjonalitetskonstanten og uttrykket som definerer funksjonen, gitt grafen.
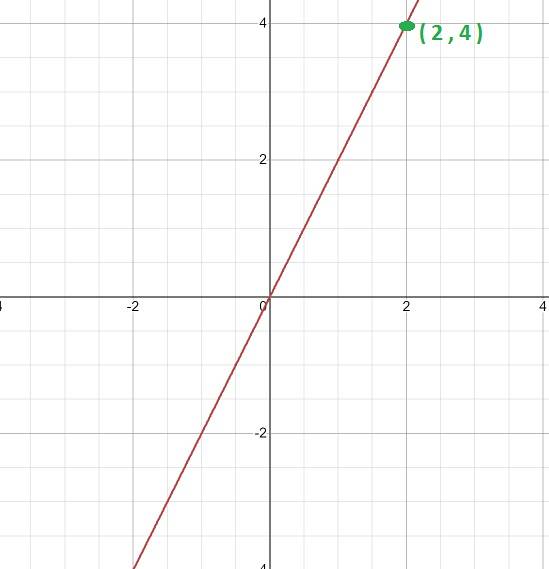
Først analyseres grafen, og dens lineære karakter er tydelig. Dette indikerer at det er en funksjon med direkte proporsjonalitet og at verdien av K vil bli oppnådd gjennom uttrykket k = y / x
Deretter velges et bestemmbart punkt fra grafen, det vil si et der koordinatene som komponerer det kan sees nøyaktig..
For dette tilfellet er poenget (2, 4) tatt. Fra hvor vi kan etablere følgende forhold.
K = 4/2 = 2
Så uttrykket er definert av funksjonen y = kx, som i dette tilfellet vil være
F (x) = 2x
Ingen har kommentert denne artikkelen ennå.