
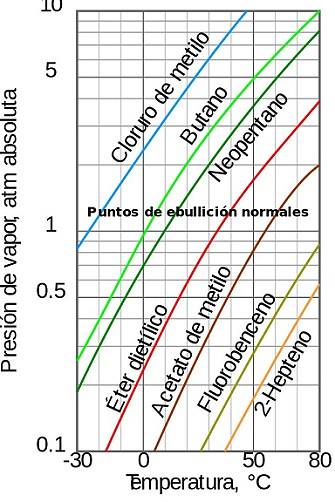
Antoines konstanter formler, ligninger, eksempler
De Antoines konstanter er tre parametere som vises i et empirisk forhold mellom metningens damptrykk og temperatur for rene stoffer. De avhenger av hvert stoff og antas å være konstante i et bestemt temperaturområde.
Utenfor dette området endrer Antoines konstanter verdien. Konstantene er relatert av en ligning opprettet i 1888 av den franske ingeniøren Louis Charles Antoine (1825-1897).
Artikkelindeks
- 1 Formler og ligninger
- 2 Metningsdamp
- 3 Hvordan beregnes Antoines konstanter??
- 4 Eksempler
- 4.1 Eksempel 1
- 4.2 Eksempel 2
- 4.3 Løsning
- 5 Referanser
Formler og ligninger
Den vanligste måten å uttrykke Antoine-funksjonen er:
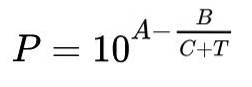
I denne formelen representerer P metningens damptrykk uttrykt i millimeter kvikksølv (mmHg), T er temperaturen som har vært den uavhengige variabelen og uttrykkes i ℃.
A, B og C er konstanter eller parametere for Antoines formel.
Viktigheten av denne formelen, som til tross for at den er empirisk, gir et enkelt analytisk uttrykk som lett kan brukes i termodynamiske beregninger..
Antoines formel er ikke unik, det er mer presise uttrykk som er utvidelser av denne formelen, men med den ulempen at de har seks eller flere parametere og deres matematiske uttrykk er mer komplekst, noe som gjør dem upraktiske å bruke i termodynamiske beregninger..
Metningsdamp
Siden Antoines formel måler metningens damptrykk, er det nødvendig å forklare hva den består av.
En væske plasseres i en glassampulle eller annen beholder. All luft fjernes fra blæren. Enheten plasseres i et termisk bad til likevekt er nådd..
I begynnelsen er alt flytende, men fordi det er et vakuum, begynner de raskere molekylene å forlate væsken og danne en gass av samme stoff som væsken..
Ovennevnte prosess er fordampning og når det skjer, øker damptrykket.
Noen av dampmolekylene mister energi og slutter seg til stoffets flytende fase, dette er prosessen med kondensasjon.
Deretter oppstår to prosesser samtidig, fordampning og kondens. Når et like antall molekyler kommer ut av væsken som de er innlemmet i, a dynamisk balanse og i dette øyeblikk oppstår det maksimale damptrykket kjent som metningstrykk.
Det er dette dampmetningstrykket Antoines formel forutsier for hvert stoff og hver temperatur..
I noen faste stoffer oppstår et lignende fenomen når man går fra den faste fasen til den gassfasen direkte uten å gå gjennom væskefasen, i disse tilfellene kan også et metningens damptrykk måles.
Det er ikke lett å etablere en teoretisk modell med utgangspunkt i de første prinsippene, siden endringer i molekylær kinetisk energi er involvert, som kan være translationell, rotasjon og vibrasjon, med den indre energien til molekylær binding. Det er av denne grunn at i praksis brukes empiriske formler.
Hvordan beregnes Antoines konstanter??
Det er ingen teoretisk metode for å oppnå Antoines konstanter, siden det er et empirisk forhold.
De er hentet fra eksperimentelle data for hvert stoff og justerer de tre parametrene A, B og C, slik at de minimerer den kvadratiske forskjellen (minste kvadraters metode) av prediksjonen med de eksperimentelle dataene..
For sluttbrukeren, som generelt er kjemiske ingeniører, er det tabeller i kjemihåndbøkene der disse konstantene er gitt for hvert stoff, som indikerer de maksimale og minste temperaturområdene de gjelder for..
Det er også tilgjengelige online-tjenester som gir verdiene til konstantene A, B og C slik tilfellet er med DDBST GmbH Onlines Services.
Det kan være mer enn ett gyldig temperaturområde for det samme stoffet. Avhengig av arbeidsområde, velges en eller annen gruppe konstanter.
Det kan oppstå vanskeligheter hvis arbeidsområdet for temperaturer er mellom to gyldighetsområder for konstantene, fordi trykkforutsigelsene med formelen ikke faller sammen i randsonen.
Eksempler
Eksempel 1
Finn damptrykket til vannet ved 25 ℃.
Løsning
Vi konsulterer tabellene for å bestemme konstantene til Antoine.
Det er to områder for vann:
Mellom 1 ℃ og 100 ℃ og mellom 99 ℃ opp til 374 ℃.
Siden vi er interessert i 25 ℃ tar vi det første området der verdien av Antoines konstanter er:
A = 8,07131
B = 1730,63
C = 233,426
P = 10 ^ (8.07131 - 1730.63 / (25 + 233.426))
Beregning av eksponenten
La oss først beregne eksponenten: 1.374499
P = 10 ^ 1,374499 = 23,686 mmHg = 0,031166 atm
Resultatanalyse
Disse resultatene tolkes slik:
Anta at rent vann blir plassert i en lufttett beholder hvorfra luften er fjernet ved hjelp av en vakuumpumpe..
Beholderen med vannet plasseres i et termisk bad ved en temperatur på 25 ℃ til den når termisk likevekt..
Vannet i den hermetiske beholderen fordamper delvis til det når metningens damptrykk, som ikke er noe annet enn trykket der den dynamiske likevekten mellom vannfasen og dampfasen blir etablert..
Dette trykket viste seg i dette tilfellet å være 0,031166 atm ved 25 ℃.
Eksempel 2
Finn damptrykket til vannet ved 100 ℃.
Løsning
Vi konsulterer tabellene for å bestemme Antoines konstanter. Det er to områder for vann:
Mellom 1 ℃ og 100 ℃ og mellom 99 ℃ opp til 374 ℃.
I dette tilfellet er temperaturen av interesse i de to områdene.
Vi bruker det første av områdene [1 ℃, 100 ℃]
A = 8,07131
B = 1730,63
C = 233,426
P = 10 ^ (8.07131 - 1730.63 / (100 + 233.426))
Beregning av eksponenten
La oss først beregne eksponenten: 2.8808
P = 10 ^ 1,374499 = 760,09 mmHg = 1.0001 atm
Deretter bruker vi det andre av områdene [99 ℃, 374 ℃]
I dette tilfellet er konstantene det
A = 8.14019
B = 1810,94
C = 244,485
P = 10 ^ (8.14019 - 1810.94 / (100 + 244.485))
La oss først beregne eksponenten: 2.88324
P = 10 ^ 2.88324 = 764.2602 mmHg = 1.0056 atm
Det er en prosentvis forskjell mellom de to resultatene på 0,55%.
Referanser
- Anvendelse av Raoult og Daltons lover og Antoines ligning. Gjenopprettet fra: misapuntesyantación.wordpress.com
- Antoines formel online kalkulator. Gjenopprettet fra: ddbonline.ddbst.de/AntoineCalculation/AntoineCalculationCGI.exe
- Gecousb. Termodynamikk og dampbord / Antoines konstanter. Gjenopprettet fra: gecousb.com.ve
- Termiske egenskaper av materie. Gjenopprettet fra: webserver.dmt.upm.es
- Yaws og Yang. Antoine-konstanttabeller for over 700 organiske forbindelser. Gjenopprettet fra: user.eng.umd.edu
- Wikipedia. Antoines ligning. Gjenopprettet fra wikipedia.com
- Wikipedia. Clausius-Clapeyron-ligning. Gjenopprettet fra wikipedia.com
- Wisniak J. Historisk utvikling av damptrykksligningen fra dalton til antoine. Gjenopprettet fra: link.springer.com

Ingen har kommentert denne artikkelen ennå.