Hva er funksjonsperioden y = 3sen (4x)?

De periode for funksjonen y = 3sen (4x) er 2π / 4 = π / 2. For å forstå årsaken til denne uttalelsen, må definisjonen av perioden for en funksjon og perioden for funksjonen sin (x) være kjent; litt på grafering av funksjoner vil også være nyttig.

Trigonometriske funksjoner, som sinus og cosinus (sin (x) og cos (x)), er veldig nyttige i både matematikk og ingeniørfag.

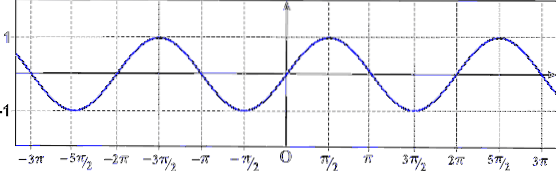
Ordet periode refererer til gjentakelse av en hendelse, så å si at en funksjon er periodisk tilsvarer å si "grafen er repetisjon av et stykke kurve." Som det kan sees i forrige bilde, er funksjonen sin (x) periodisk.

Periodiske funksjoner

En funksjon f (x) sies å være periodisk hvis det eksisterer en reell verdi p ≠ 0 slik at f (x + p) = f (x) for alle x i domenet til funksjonen. I dette tilfellet er funksjonstiden s.

Perioden av funksjonen kalles vanligvis det minste positive reelle tallet p som tilfredsstiller definisjonen.

Som det kan sees i forrige graf, er funksjonen sin (x) periodisk og perioden er 2π (cosinusfunksjonen er også periodisk, med en periode lik 2π).

Endringer i grafen til en funksjon

La f (x) være en funksjon hvis graf er kjent, og la c være en positiv konstant. Hva skjer med grafen til f (x) hvis f (x) multipliseres med c? Med andre ord, hva er grafen til c * f (x) og f (cx)?

Graf av c * f (x)

Når du multipliserer en funksjon, eksternt, med en positiv konstant, gjennomgår grafen til f (x) en endring i utgangsverdiene; det vil si at endringen er vertikal og det er to tilfeller:

- Hvis c> 1, gjennomgår grafen en vertikal strekning med faktoren c.

- Ja 0

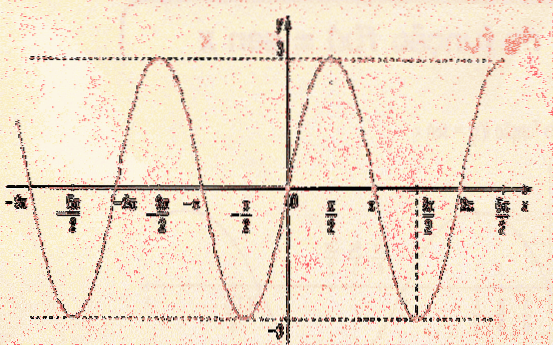
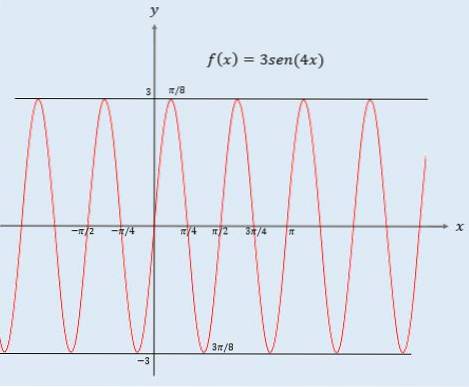
Graf av f (cx)

Når argumentet til en funksjon multipliseres med en konstant, gjennomgår grafen til f (x) en endring i inngangsverdiene; det vil si at endringen er horisontal, og som før kan det være to tilfeller:

- Hvis c> 1, gjennomgår grafen horisontal kompresjon med faktoren 1 / c.

- Ja 0

Funksjonens periode y = 3sen (4x)

Det skal bemerkes at i funksjonen f (x) = 3sen (4x) er det to konstanter som endrer grafen til sinusfunksjonen: den ene multipliserer eksternt og den andre internt..

3 som er utenfor sinusfunksjonen hva den gjør er å forlenge funksjonen vertikalt med faktoren 3. Dette innebærer at grafen for funksjon 3 sin (x) vil være mellom verdiene -3 og 3.

4 inni sinusfunksjonen får grafen til funksjonen til å gjennomgå horisontal kompresjon med en faktor på 1/4.

På den annen side måles en funksjons periode horisontalt. Siden perioden av funksjonen sin (x) er 2π, vurderer sin (4x) størrelsen på perioden.

For å finne ut hvilken periode y = 3sen (4x) er, bare multipliser perioden for funksjonen sin (x) med 1/4 (kompresjonsfaktoren).

Perioden for funksjonen y = 3sin (4x) er med andre ord 2π / 4 = π / 2, som man kan se i den siste grafen.

Referanser

1. Fleming, W., & Varberg, D. E. (1989). Precalculus matematikk. Prentice Hall PTR.
2. Fleming, W., & Varberg, D. E. (1989). Precalculus matematikk: en problemløsende tilnærming (2, Illustrert utg.). Michigan: Prentice Hall.
3. Larson, R. (2010). Precalculus (8. utgave). Cengage læring.
4. Pérez, C. D. (2006). Forberegning. Pearson Education.
5. Purcell, E. J., Varberg, D., og Rigdon, S. E. (2007). Beregning (9. utg.). Prentice hall.
6. Saenz, J. (2005). Differensiell kalkulator med tidlige transcendente funksjoner for vitenskap og ingeniørfag (Andre utgave utg.). Hypotenuse.
7. Sullivan, M. (1997). Forberegning. Pearson Education.