Moody diagramligninger, hva det er til, applikasjoner

De humørfylt diagram består av en serie kurver tegnet på logaritmisk papir, som brukes til å beregne friksjonsfaktoren i strømmen av en turbulent væske gjennom en sirkulær kanal.

Med friksjonsfaktor F friksjon energitap blir evaluert, en viktig verdi for å bestemme riktig ytelse for pumper som distribuerer væsker som vann, bensin, råolje og andre.

For å kjenne energien i strømmen av en væske, er det nødvendig å kjenne gevinster og tap på grunn av faktorer som hastighet, høyde, tilstedeværelsen av enheter (pumper og motorer), effekten av væskens viskositet og friksjon mellom den. veggene på røret.

Artikkelindeks

• 1 Ligninger for energien til en væske i bevegelse
  • 1.1 -Friksjonsfaktor og Reynolds-nummer
• 2 Hva er det til?
• 3 Hvordan lages den og hvordan brukes den??
  • 3.1 - Arbeidet eksempel 1
• 4 Søknader
  • 4.1 -Løst eksempel 2
• 5 Referanser

Ligninger for energien til en flytende væske

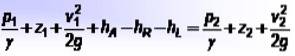
- s₁ Y s_to er trykket på hvert punkt,

- z₁ Y z_to er høydene med hensyn til referansepunktet,

- v₁ Y v_to er de respektive væskehastigheter,

- h_TIL er energien tilført av pumper, h_R er energien som tas av noen enheter, for eksempel en motor, og h_L dekker væskeenergitap på grunn av friksjon mellom væske- og rørveggene, samt andre mindre tap.

Verdien av h_L beregnes ved hjelp av Darcy-Weisbach-ligningen:

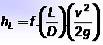
Hvor L er lengden på røret, D er dens innvendige diameter, v er væskens hastighet og g er verdien av akselerasjonen på grunn av tyngdekraften. Dimensjonene på h_L er lengde, og vanligvis er enhetene det er representert meter eller fot.

-Friksjonsfaktor og Reynolds-nummer

Å beregne F empiriske ligninger hentet fra eksperimentelle data kan brukes. Det er nødvendig å skille om det er en væske i et laminært regime eller i et turbulent regime. For det laminære regimet F enkelt evaluert:

f = 64 / N_R

Hvor N_R er Reynolds-tallet, hvis verdi avhenger av regimet der væsken er. Kriteriene er:

Laminær strømning: N_R < 2000 el flujo es laminar; Flujo turbulento N_R > 4000; Overgangsregime: 2000 < N_R < 4000

Reynolds-tallet (dimensjonsløst) avhenger i sin tur av hastigheten på væsken v, rørets indre diameter D og kinematisk viskositet n av væsken, hvis verdi oppnås ved hjelp av tabeller:

N_R = v.D / n

Colebrook ligning

For en turbulent strømning er den mest aksepterte ligningen i kobber- og glassrør Cyril Colebrook (1910-1997), men den har ulempen at F det er ikke eksplisitt:

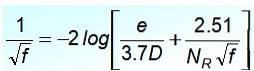
I denne ligningen kvotienten e / D er den relative ruheten til røret og N_R er Reynolds-nummeret. En nøye observasjon viser at det ikke er lett å la F til venstre for likestillingen, så det er ikke egnet for umiddelbare beregninger.

Colebrook selv foreslo denne tilnærmingen, som er eksplisitt, gyldig med noen begrensninger:

Hva er den til?

Moody-diagrammet er nyttig for å finne friksjonsfaktoren F inkludert i Darcys ligning, siden det i Colebrooks ligning ikke er lett å uttrykke F direkte når det gjelder andre verdier.

Dens bruk forenkler å skaffe verdien av F, ved å inneholde den grafiske representasjonen av F i funksjon av N_R for forskjellige verdier av relativ ruhet på en logaritmisk skala.

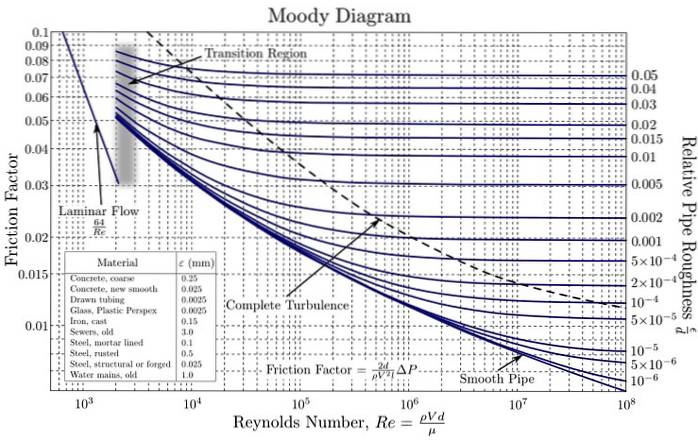
Disse kurvene er laget fra eksperimentelle data med forskjellige materialer som ofte brukes i rørfabrikasjon. Ved hjelp av en logaritmisk skala for begge F som for N_R det er nødvendig, siden de dekker et veldig bredt spekter av verdier. På denne måten forenkles graftegningen av verdier av forskjellige størrelsesordener..

Den første grafen av Colebrook-ligningen ble oppnådd av ingeniøren Hunter Rouse (1906-1996) og kort tid etter ble den modifisert av Lewis F. Moody (1880-1953) i den formen den brukes i dag..

Den brukes til både sirkulære og ikke-sirkulære rør, bare erstatte den hydrauliske diameteren for disse.

Hvordan lages den og hvordan brukes den??

Som forklart ovenfor er Moody-diagrammet laget av mange eksperimentelle data, presentert i grafisk form. Her er trinnene for å bruke den:

- Beregn Reynolds-nummer N_R for å bestemme om strømningen er laminær eller turbulent.

- Beregn den relative ruheten ved hjelp av ligningen og_r = e / D, hvor og er den absolutte ruheten til materialet og D er rørets indre diameter. Disse verdiene er oppnådd gjennom tabeller.

- Nå som du har gjort det og_r Y N_R, projiser vertikalt til du når kurven som tilsvarer og_r oppnådd.

- Projiser horisontalt og til venstre for å lese verdien av F.

Et eksempel vil hjelpe deg med å enkelt visualisere hvordan diagrammet brukes.

-Arbeidet eksempel 1

Bestem friksjonsfaktoren for vann ved 160 ° F som strømmer med en hastighet på 22 ft / s i en kanal laget av ubelagt smijern med en innvendig diameter på 1 tommer..

Løsning

Nødvendige data (finnes i tabeller):

Kinematisk viskositet av vann ved 160 ºF: 4,38 x 10^-6 fot^to/ s

Absolutt ruhet av ubelagt smijern: 1,5 x 10 ^-4 føtter

Første skritt

Reynolds-tallet beregnes, men ikke før den indre diameteren overføres fra 1 tomme til fot:

1 tomme = 0,0833 fot

N_R = (22 x 0,0833) / 4,38 x 10^-6= 4,18 x 10 ⁵

I henhold til kriteriene som er vist før, er det en turbulent strømning, så gjør Moody-diagrammet det mulig å oppnå den tilsvarende friksjonsfaktoren uten å måtte bruke Colebrook-ligningen.

Andre trinn

Du må finne den relative grovheten:

og_r = 1,5 x 10 -4 / 0,0833 = 0,0018

Tredje trinn

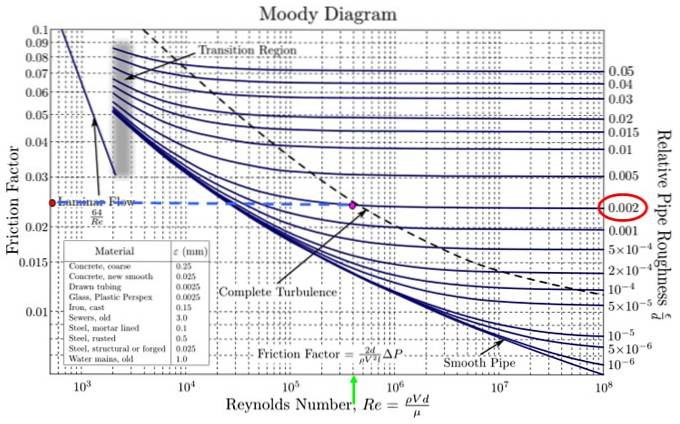
I det medfølgende Moody-diagrammet er det nødvendig å gå ytterst til høyre og finne den nærmeste relative ruheten til verdien som oppnås. Det er ingen som tilsvarer nøyaktig 0,0018, men det er en som er ganske nær, den på 0,002 (rød oval i figuren).

Samtidig søkes det tilsvarende Reynolds-nummeret på den horisontale aksen. Den nærmeste verdien til 4,18 x 10 ⁵ er 4 x 10 ⁵ (grønn pil i figuren). Krysset mellom begge er fuchsia-punktet.

Fjerde trinn

Projiser til venstre etter den blå prikkede linjen og nå det oransje punktet. Beregn nå verdien av F, tar i betraktning at divisjonene ikke er like store som de er en logaritmisk skala på både den horisontale og vertikale aksen.

Moody-diagrammet gitt i figuren har ikke fine horisontale inndelinger, derfor verdien av F i 0,024 (det er mellom 0,02 og 0,03, men det er ikke halvparten, men litt mindre).

Det er kalkulatorer på nettet som bruker Colebrook-ligningen. En av dem (se referanser) ga verdien 0,023664639 for friksjonsfaktoren.

applikasjoner

Moody-diagrammet kan brukes til å løse tre typer problemer, forutsatt at væsken og den absolutte ruheten til røret er kjent:

- Beregning av trykkfall eller trykkforskjell mellom to punkter, gitt lengden på røret, høydeforskjellen mellom de to punktene som skal vurderes, hastigheten og den indre diameteren på røret.

- Bestemmelse av strømning, med kunnskap om lengden og diameteren på røret, pluss det spesifikke trykkfallet.

- Evaluering av rørets diameter når lengde, strømning og trykkfall mellom punktene som skal vurderes er kjent.

Problemer av den første typen løses direkte ved hjelp av diagrammet, mens de av den andre og tredje typen krever bruk av en datapakke. For eksempel i den tredje typen, hvis diameteren på røret ikke er kjent, kan Reynolds-tallet ikke vurderes direkte, heller ikke den relative grovheten..

En måte å løse dem på er å anta en innvendig innvendig diameter og derfra justere verdiene suksessivt for å oppnå det trykkfall som er spesifisert i problemet..

-Arbeidet eksempel 2

Du har 160 ° F vann som strømmer jevnt og trutt langs et 1-tommers ubelagt rør av smijern med en hastighet på 22 ft / s. Bestem trykkforskjellen forårsaket av friksjon og pumpekraften som kreves for å opprettholde flyt i en lengde på horisontalt rør L = 200 fot langt..

Løsning

Nødvendige data: tyngdeakselerasjonen er 32 fot / s^to ; den spesifikke tyngdekraften til vann ved 160 ºF er γ = 61,0 lb-kraft / fot³

Dette er røret fra løst eksempel 1, derfor er friksjonsfaktoren allerede kjent F, som er estimert til 0,0024. Denne verdien blir tatt med i Darcy-ligningen for å evaluere friksjonstap:

Nødvendig pumpekraft er:

W = v. A. (s₁ - s_to)

Der A er rørets tverrsnittsareal: A = p. (D^to/ 4) = s. (0,0833^to/ 4) fot^to = 0,00545 fot^to

W = 22 fot / s. 2659,6 lb-kraft / fot^to. 0,00545 fot^to= 318,9 lb-kraft. føtter

Kraft uttrykkes best i watt, hvor konverteringsfaktoren kreves:

1 Watt = 0.737 lb-kraft. føtter

Derfor er kraften som kreves for å opprettholde flyten W = 432,7 W

Referanser

1. Cimbala, C. 2006. Fluid Mechanics, Fundamentals and Applications. Mc. Graw Hill. 335- 342.
2. Franzini, J. 1999. Fluid Mechanics with Application is in Engineering. Mc. Graw Hill. 176-177.
3. LMNO Engineering. Moody Friction Factor Calculator. Gjenopprettet fra: lmnoeng.com.
4. Mott, R. 2006. Væskemekanikk. 4. plass Utgave. Pearson Education. 240-242.
5. Engineering Toolbox. Moody Diagram. Gjenopprettet fra: engineeringtoolbox.com
6. Wikipedia. Moody Chart. Gjenopprettet fra: en.wikipedia.org