
Distribusjon F egenskaper og øvelser løst
De F distribusjon o Fisher-Snedecor-fordelingen er den som brukes til å sammenligne avvikene til to forskjellige eller uavhengige populasjoner, som hver følger en normalfordeling.
Fordelingen som følger variansen til et sett med prøver fra en enkelt normalpopulasjon, er chi-kvadratfordelingen (Χto) av grad n-1, hvis hver av prøvene i settet har n elementer.
For å sammenligne avvikene fra to forskjellige populasjoner, er det nødvendig å definere en statistisk, det vil si en ekstra tilfeldig variabel som lar oss se om begge populasjonene har samme varians eller ikke.
Nevnte hjelpevariabel kan være direkte kvotienten til prøvevariansene til hver populasjon, i hvilket tilfelle, hvis nevnte kvotient er nær enhet, er det bevis for at begge populasjoner har lignende varianter.
Artikkelindeks
- 1 F-statistikken og dens teoretiske fordeling
- 1.1 Gjennomsnitt, modus og varians av F-fordelingen
- 2 Håndtere F-distribusjonen
- 2.1 Tabeller over F-fordelingen
- 2.2 Programvare for F-distribusjon
- 3 Løst øvelser
- 3.1 Øvelse 1
- 3.2 Øvelse 2
- 4 Referanser
F-statistikken og dens teoretiske fordeling
Den tilfeldige variabelen F eller F-statistikk foreslått av Ronald Fisher (1890 - 1962) er den som ofte brukes til å sammenligne avvikene til to populasjoner og er definert som følger:
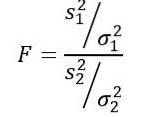
Å være sto prøven varians og σto populasjonsavviket. For å skille hver av de to befolkningsgruppene brukes henholdsvis abonnement 1 og 2..
Det er kjent at chi-kvadratfordelingen med (n-1) frihetsgrader er den som følger den ekstra (eller statistiske) variabelen definert nedenfor:
Xto = (n-1) sto / σto.
Derfor følger F-statistikken en teoretisk fordeling gitt av følgende formel:
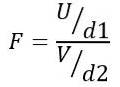
Å være ELLER kikvadratfordelingen med d1 = n1 - 1 frihetsgrader for befolkning 1 og V kikvadratfordelingen med d2 = n2 - 1 frihetsgrader for befolkningen 2.
Kvotienten definert på denne måten er en ny sannsynlighetsfordeling, kjent som F distribusjon med d1 frihetsgrader i teller og d2 frihetsgrader i nevneren.
Gjennomsnitt, modus og varians av F-fordelingen
Halv
Gjennomsnittet av F-fordelingen beregnes som følger:
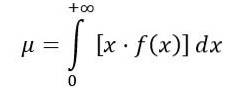
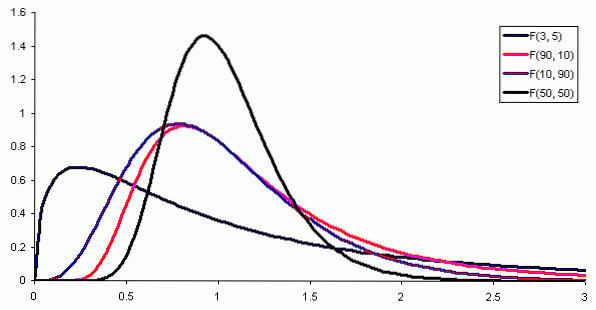
Der f (x) er sannsynlighetstettheten til F-fordelingen, som er vist i figur 1 for forskjellige kombinasjoner av parametere eller frihetsgrader.
Vi kan skrive sannsynlighetstettheten f (x) som en funksjon av funksjonen Γ (gammafunksjon):
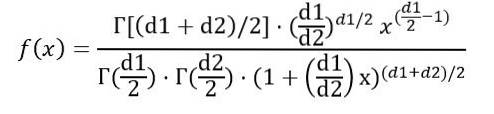
Når integralen angitt ovenfor er utført, konkluderes det med at gjennomsnittet av F-fordelingen med frihetsgrader (d1, d2) er:
μ = d2 / (d2 - 2) med d2> 2
Der det bemerkes at merkelig nok ikke middelet avhenger av tellerens frihetsgrader d1.
mote
På den annen side avhenger modusen av d1 og d2 og er gitt av:
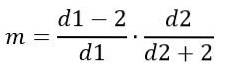
For d1> 2.
Variasjon av F-fordelingen
Avviket σto av F-fordelingen beregnes fra integralen:
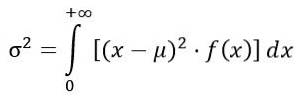
Å skaffe:
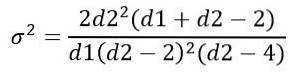
Håndtering av F-distribusjon
Som andre kontinuerlige sannsynlighetsfordelinger som involverer kompliserte funksjoner, blir håndteringen av F-distribusjonen gjort ved hjelp av tabeller eller programvare..
Fordelingstabeller F
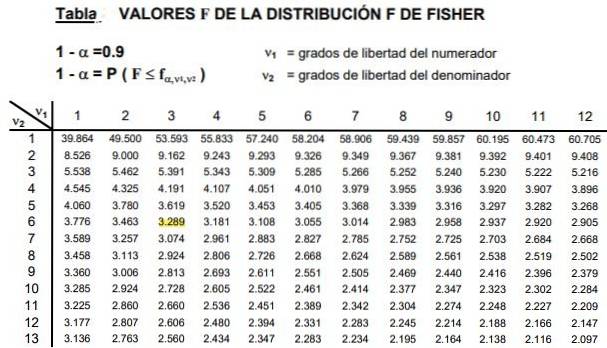
Tabellene involverer de to parametrene eller frihetsgrader for F-fordelingen, kolonnen angir tellerens frihetsgrad og raden graden av frihet for nevneren.
Figur 2 viser et snitt av tabellen over F-fordelingen for saken a Signifikansnivå på 10%, det vil si α = 0,1. Verdien av F er uthevet når d1 = 3 og d2 = 6 med selvtillitsnivå 1- α = 0,9 det vil si 90%.
Programvare for F-distribusjon
Når det gjelder programvaren som håndterer F-distribusjonen, er det et stort utvalg, fra regneark som dette utmerke til spesialiserte pakker som minitab, SPSS Y R for å nevne noen av de mest kjente.
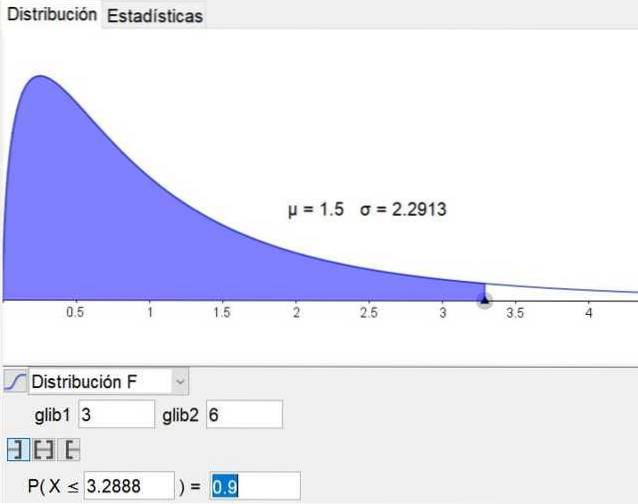
Det er bemerkelsesverdig at geometri og matematikk programvare geogebra har et statistisk verktøy som inkluderer hovedfordelingene, inkludert F-fordelingen. Figur 3 viser F-fordelingen for saken d1 = 3 og d2 = 6 med selvtillitsnivå på 90%.
Løst øvelser
Øvelse 1
Vurder to eksempler på populasjoner som har samme populasjonsvarians. Hvis prøve 1 har størrelse n1 = 5 og prøve 2 har størrelse n2 = 10, bestem den teoretiske sannsynligheten for at kvotienten for deres respektive varians er mindre enn eller lik 2.
Løsning
Det skal huskes at F-statistikken er definert som:
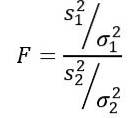
Men vi blir fortalt at populasjonsavvikene er like, så for denne øvelsen gjelder følgende:
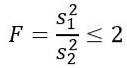
Ettersom vi vil vite den teoretiske sannsynligheten for at denne kvoten av prøvevariasjoner er mindre enn eller lik 2, må vi kjenne området under F-fordelingen mellom 0 og 2, som kan oppnås ved tabeller eller programvare. For dette må det tas i betraktning at den nødvendige F-fordelingen har d1 = n1 - 1 = 5 - 1 = 4 og d2 = n2 - 1 = 10 - 1 = 9, det vil si F-fordelingen med frihetsgrader ( 4, 9).
Ved å bruke det statistiske verktøyet til geogebra Det ble bestemt at dette arealet er 0,82, så det konkluderes med at sannsynligheten for at kvotienten for prøvevariasjoner er mindre enn eller lik 2 er 82%.
Trening to
Det er to produksjonsprosesser for tynne ark. Variasjonen i tykkelsen skal være så lav som mulig. Det tas 21 prøver fra hver prosess. Prøven fra prosess A har et standardavvik på 1,96 mikron, mens prøven fra prosess B har et standardavvik på 2,13 mikron. Hvilke av prosessene har minst variasjon? Bruk et avvisningsnivå på 5%.
Løsning
Dataene er som følger: Sb = 2,13 med nb = 21; Sa = 1,96 med na = 21. Dette betyr at vi må jobbe med en F-fordeling på (20, 20) frihetsgrader.
Nullhypotesen innebærer at populasjonsvariansen til begge prosessene er identisk, det vil si σa ^ 2 / σb ^ 2 = 1. Den alternative hypotesen vil innebære forskjellige populasjonsavvik.
Deretter, under antagelse av identiske populasjonsavvik, er den beregnede F-statistikken definert som: Fc = (Sb / Sa) ^ 2.
Siden avvisningsnivået er tatt som α = 0,05, da er α / 2 = 0,025
Fordelingen F (0,025, 20,20) = 0,406, mens F (0,975, 20,20) = 2,46.
Derfor vil nullhypotesen være sant hvis den beregnede F oppfyller: 0.406≤Fc≤2.46. Ellers avvises nullhypotesen.
Som Fc = (2.13 / 1.96) ^ 2 = 1.18 konkluderes det med at Fc-statistikken ligger i akseptområdet for nullhypotesen med en sikkerhet på 95%. Med andre ord, med 95% sikkerhet, har begge produksjonsprosesser samme populasjonsvarians..
Referanser
- F Test for uavhengighet. Gjenopprettet fra: saylordotorg.github.io.
- Med Wave. Statistikk anvendt på helsevitenskap: F-testen. Hentet fra: medwave.cl.
- Sannsynligheter og statistikk. Distribusjon F. Gjenopprettet fra: probayestadistica.com.
- Triola, M. 2012. Elementær statistikk. 11. Utgave. Addison Wesley.
- UNAM. Distribusjon F. Gjenopprettet fra: asesorias.cuautitlan2.unam.mx.
- Wikipedia. Distribusjon F. Gjenopprettet fra: es.wikipedia.com



Ingen har kommentert denne artikkelen ennå.