
Diskrete sannsynlighetsfordelingskarakteristikker, øvelser
De diskrete sannsynlighetsfordelinger de er en funksjon som tildeler hvert element av X (S) = x1, x2,…, xi, ..., hvor X er en gitt diskret tilfeldig variabel og S er dens prøverom, sannsynligheten for at nevnte hendelse inntreffer. Denne funksjonen f av X (S) definert som f (xi) = P (X = xi) kalles noen ganger sannsynlighetsmassefunksjonen.
Denne massen av sannsynligheter er generelt representert i tabellform. Siden X er en diskret tilfeldig variabel, har X (S) et endelig antall hendelser eller teller uendelig. Blant de vanligste diskrete sannsynlighetsfordelingene har vi den jevne fordelingen, binomialfordelingen og Poisson-fordelingen.
Artikkelindeks
- 1 Funksjoner
- 2 typer
- 2.1 Ensartet fordeling over n poeng
- 2.2 Binomial fordeling
- 2.3 Poissonfordeling
- 2.4 Hypergeometrisk fordeling
- 3 Løst øvelser
- 3.1 Første øvelse
- 3.2 Andre øvelse
- 3.3 Tredje øvelse
- 3.4 Tredje øvelse
- 4 Referanser
Kjennetegn
Sannsynlighetsfordelingsfunksjonen må oppfylle følgende betingelser:
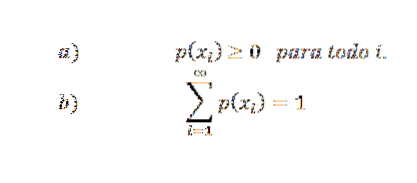
Videre, hvis X bare tar et endelig antall verdier (for eksempel x1, x2,…, xn), så blir p (xi) = 0 hvis i> ny, derfor blir den uendelige serien av tilstand b en endelig serie.
Denne funksjonen oppfyller også følgende egenskaper:
La B være en hendelse assosiert med den tilfeldige variabelen X. Dette betyr at B er inneholdt i X (S). Anta spesifikt at B = xi1, xi2,…. Derfor:
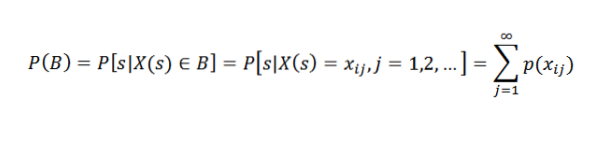
Med andre ord: sannsynligheten for en hendelse B er lik summen av sannsynlighetene for de individuelle resultatene knyttet til B.
Fra dette kan vi konkludere med at hvis a < b, los sucesos (X ≤ a) y (a < X ≤ b) son mutuamente excluyentes y, además, su unión es el suceso (X ≤ b), por lo que tenemos:
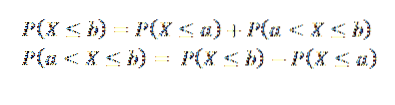
Typer
Jevn fordeling over n poeng
En tilfeldig variabel X sies å følge en fordeling som er karakterisert ved å være jevn på n poeng hvis hver verdi er tildelt samme sannsynlighet. Sannsynlighetsmassefunksjonen er:
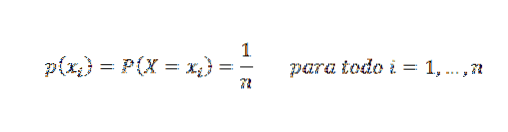
Anta at vi har et eksperiment som har to mulige utfall, det kan være kastet av en mynt hvis mulige utfall er hoder eller haler, eller valget av et heltall hvis resultat kan være et partall eller et oddetall; denne typen eksperimenter er kjent som Bernoulli-tester.
Generelt kalles de to mulige resultatene suksess og fiasko, hvor p er sannsynligheten for suksess og 1-p er sannsynligheten for fiasko. Vi kan bestemme sannsynligheten for x suksesser i n Bernoulli tester som er uavhengige av hverandre med følgende fordeling.
Binomial fordeling
Det er funksjonen som representerer sannsynligheten for å oppnå x suksesser i n uavhengige Bernoulli tester, hvis sannsynlighet for suksess er p. Sannsynlighetsmassefunksjonen er:
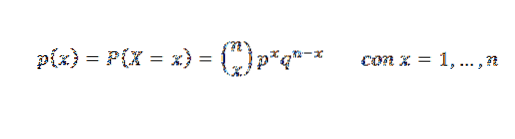
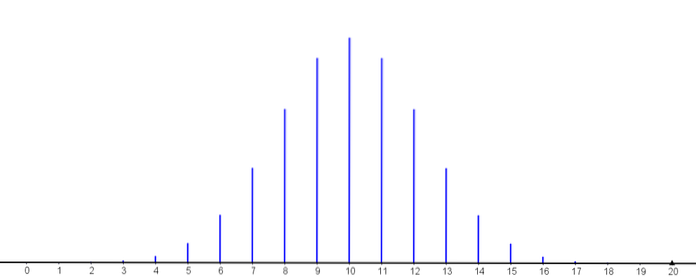
Grafen nedenfor representerer sannsynlighetsmassefunksjonen for forskjellige verdier av parametrene for binomialfordelingen.
Den følgende distribusjonen skylder navnet til den franske matematikeren Simeon Poisson (1781-1840), som fikk den som grensen for binomialfordelingen..
Poisson-fordeling
En tilfeldig variabel X sies å ha en Poisson-fordeling av parameteren λ når den kan ta de positive heltallverdiene 0,1,2,3, ... med følgende sannsynlighet:
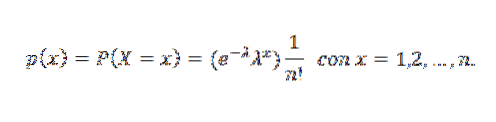
I dette uttrykket er λ gjennomsnittstallet som tilsvarer forekomsten av hendelsen for hver tidsenhet, og x er antall ganger hendelsen skjer.
Sannsynlighetsmassefunksjonen er:
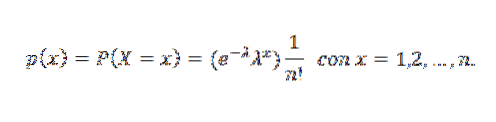
Deretter en graf som representerer sannsynlighetsmassefunksjonen for forskjellige verdier av parametrene til Poisson-fordelingen.
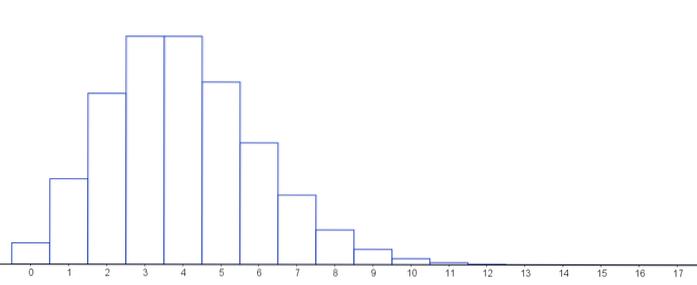
Vær oppmerksom på at så lenge antallet suksesser er lavt og antall tester som er utført på en binomialfordeling er høy, kan vi alltid tilnærme disse fordelingen, da Poisson-fordelingen er grensen for binomialfordelingen..
Hovedforskjellen mellom disse to distribusjonene er at mens binomialet avhenger av to parametere - nemlig n og p-, avhenger Poisson bare av λ, som noen ganger kalles distribusjonsintensiteten..
Så langt har vi bare snakket om sannsynlighetsfordelinger for tilfeller der de forskjellige eksperimentene er uavhengige av hverandre; det vil si når resultatet av en ikke påvirkes av noe annet resultat.
Når tilfellet med eksperimenter som ikke er uavhengige forekommer, er den hypergeometriske fordelingen veldig nyttig.
Hypergeometrisk fordeling
La N være det totale antallet objekter i et endelig sett, hvor vi på en eller annen måte kan identifisere k av disse, og dermed danne en delmengde K, hvis komplement dannes av de gjenværende N-k-elementene.
Hvis vi tilfeldig velger n objekter, har den tilfeldige variabelen X som representerer antall objekter som tilhører K i nevnte valg, en hypergeometrisk fordeling av parametrene N, n og k. Sannsynlighetsmassefunksjonen er:
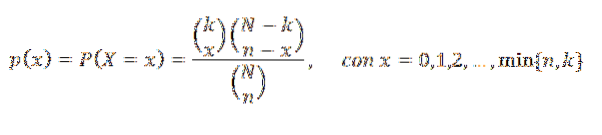
Grafen nedenfor representerer sannsynlighetsmassefunksjonen for forskjellige verdier av parametrene for den hypergeometriske fordelingen.
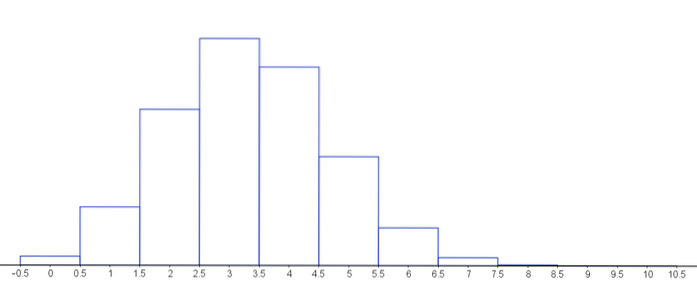
Løst øvelser
Første øvelse
Anta at sannsynligheten for at et radiorør (plassert i en bestemt type utstyr) vil fungere i mer enn 500 timer er 0,2. Hvis 20 rør testes, hva er sannsynligheten for at nøyaktig k av disse vil kjøre i mer enn 500 timer, k = 0, 1,2,…, 20?
Løsning
Hvis X er antall rør som fungerer mer enn 500 timer, vil vi anta at X har en binomial fordeling. Deretter
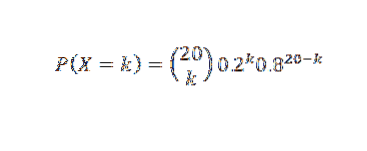
Og så:

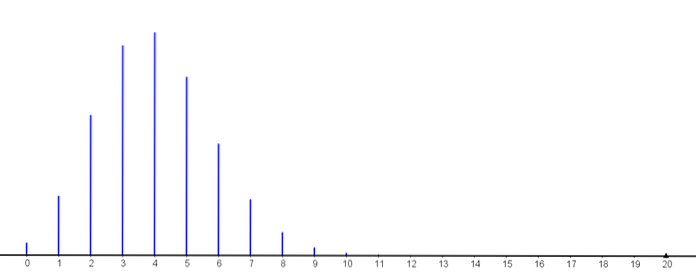
For k≥11 er sannsynlighetene mindre enn 0,001
Dermed kan vi observere hvordan sannsynligheten for at k av disse fungerer i mer enn 500 timer øker, til den når sin maksimale verdi (med k = 4) og deretter begynner å synke..
Andre øvelse
En mynt kastes 6 ganger. Når resultatet er dyrt, vil vi si at det er en suksess. Hva er sannsynligheten for at to hoder vil komme opp nøyaktig?
Løsning
For dette tilfellet har vi n = 6 og både sannsynligheten for suksess og fiasko er p = q = 1/2
Derfor er sannsynligheten for at to hoder er gitt (det vil si k = 2)
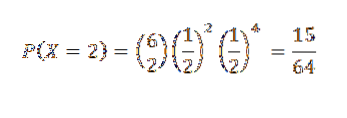
Tredje øvelse
Hva er sannsynligheten for å finne minst fire hoder?
Løsning
For dette tilfellet har vi at k = 4, 5 eller 6
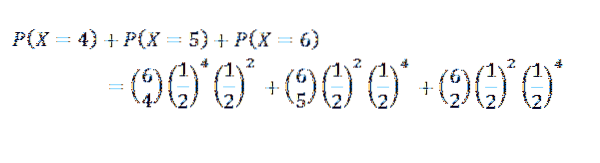
Tredje øvelse
Anta at 2% av varene produsert på en fabrikk er defekte. Finn sannsynligheten P for at det er tre defekte gjenstander i et utvalg på 100 artikler.
Løsning
I dette tilfellet kan vi bruke binomialfordelingen for n = 100 og p = 0,02, og få et resultat:
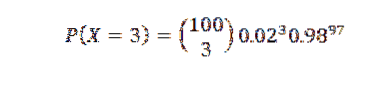
Siden p er liten, bruker vi imidlertid Poisson-tilnærmingen med λ = np = 2. A) Ja,
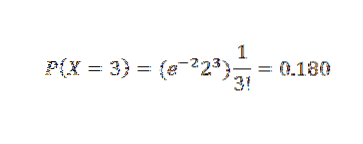
Referanser
- Kai Lai Chung. Elementær sannsynlighetsteori med stokastiske prosesser. Springer-Verlag New York Inc.
- Kenneth.H. Rosen. Diskret matematikk og dens applikasjoner. S.A. MCGRAW-HILL / INTERAMERICANA DE ESPAÑA.
- Paul L. Meyer. Sannsynlighet og statistiske applikasjoner. S.A. MEKSIKANSK ALHAMBRA.
- Seymour Lipschutz Ph.D. 2000 Løste problemer med diskret matematikk. McGRAW-HILL.
- Seymour Lipschutz Ph.D. Teori og sannsynlighetsproblemer. McGRAW-HILL.



Ingen har kommentert denne artikkelen ennå.