Andregrads ligninger formel, hvordan du løser dem, eksempler, øvelser

De kvadratiske eller kvadratiske ligninger og en ukjent har skjemaet øks^to + bx + c = 0. Der a ≠ 0, siden hvis det var 0, ville ligningen bli transformert til en lineær ligning, og koeffisientene a, b og c er reelle tall.

Det ukjente som skal bestemmes er verdien av x. For eksempel ligningen 3x^to - 5x + 2 = 0 er en fullstendig kvadratisk ligning.

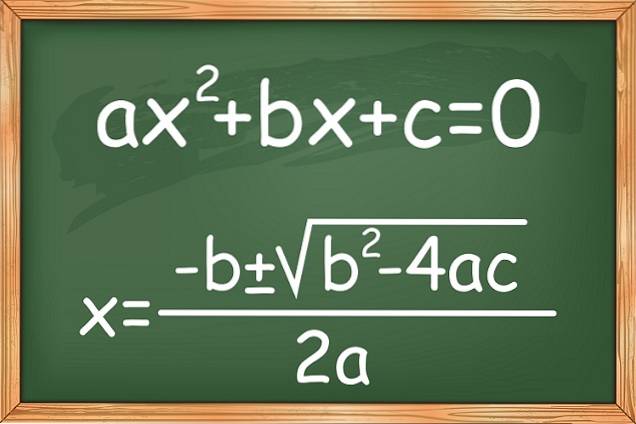
Det er også varianter som er kjent som ufullstendige andregradsligninger, som mangler noen av begrepene, bortsett fra øks^to. Her er noen eksempler:

x^to - 25 = 0

3x^to - 5x = 0

Al Juarismi, den berømte arabiske matematikeren i antikken, beskrev i sine arbeider forskjellige typer ligninger i første og andre grad, men bare med positive koeffisienter. Imidlertid var det den franske matematikeren Francois Viete som først introduserte bokstaver for å symbolisere mengder og foreslå løsningen gjennom formelen resolutt:

Dette er en generell formel som gjør det mulig å løse en kvadratisk ligning, finne dens røtter eller nuller, selv om løsningene ikke er reelle. Det er også andre måter å løse dem på.

Artikkelindeks

• 1 Hvordan løse kvadratiske ligninger?
  • 1.1 Løsning ved factoring
  • 1.2 Grafisk metode
  • 1.3 Oppløsning med vitenskapelig kalkulator
  • 1.4 Diskriminant av en kvadratisk ligning
• 2 Eksempler på enkle kvadratiske ligninger
  • 2.1 Ligning av formen x2 + mx + n = 0
  • 2.2 Ufullstendig ligning av skjemaet ax2 + c = 0
  • 2.3 Ufullstendig ligning av skjemaet ax2 + bx = 0
  • 2.4 Ligninger med nevner
  • 2.5 Høyere ordens ligninger som blir kvadratiske
• 3 Enkle løste øvelser
  • 3.1 - Øvelse 1
  • 3.2 - Øvelse 2
  • 3.3 - Øvelse 3
• 4 Referanser

Hvordan løse kvadratiske ligninger?

Ligninger av andre grad kan løses med formelen gitt ovenfor, og det er også andre algebraiske prosedyrer som kan gi resultater i noen ligninger.

Vi skal løse ligningen som ble foreslått i begynnelsen med formelen, en gyldig metode for enhver kvadratisk ligning med en ukjent:

3x^to - 5x + 2 = 0

For å bruke formelen riktig bemerker vi at:

• til er koeffisienten til begrepet med x^to
• b er koeffisienten til det lineære begrepet
• c er det uavhengige begrepet.

Vi skal identifisere dem fra samme ligning:

a = 3

b = -5

c = 2

Merk at tegnet som følger med koeffisienten må tas i betraktning. Nå erstatter vi disse verdiene i formelen:

I telleren er det symbolet "pluss - minus" ±, som indikerer at størrelsen med en rot kan tas som positiv og også som negativ. En kvadratisk ligning har høyst to virkelige løsninger, og dette symbolet tar hensyn til dette.

La oss kalle x₁ og x_to til disse to løsningene, så:

x₁ = (5 + 1) / 6 = 1

x_to = (5-1) / 6 = 4/6 = 2/3

Løsning ved factoring

Noen ligninger av andre grad består av trinomialer som lett blir beregnet på. I så fall er denne metoden mye raskere. La oss vurdere ligningen:

x^to + 7x - 18 = 0

Faktoriseringen har denne formen:

(x +) ⋅ (x -)

De tomme feltene er fylt med to tall som når multiplisert gir 18, og når de trekkes fra, gir 7. Tegnene i parentes er valgt med dette kriteriet:

-I første parentes er tegnet plassert mellom første og andre periode.

-Og i den andre parentesen er produktet av tegnene som sees.

Når det gjelder tallene, blir de lett scoret i dette tilfellet: de er 9 og 2. Den største plasseres alltid i den første parentesen, slik:

x^to + 7x - 18 = (x + 9). (x - 2)

Leseren kan verifisere ved hjelp av den fordelende egenskapen at når man utvikler produktet av høyre side av likheten, oppnås trinomialet til venstre. Nå er ligningen omskrevet:

(x + 9) ⋅ (x - 2) = 0

For at likheten skal oppfylles, er det nok at en av de to faktorene er null. Så i den første må du gjøre x₁ = -9 eller det kan være at den andre faktoren forsvinner, i så fall x_to = 2. Dette er løsningene i ligningen.

Grafisk metode

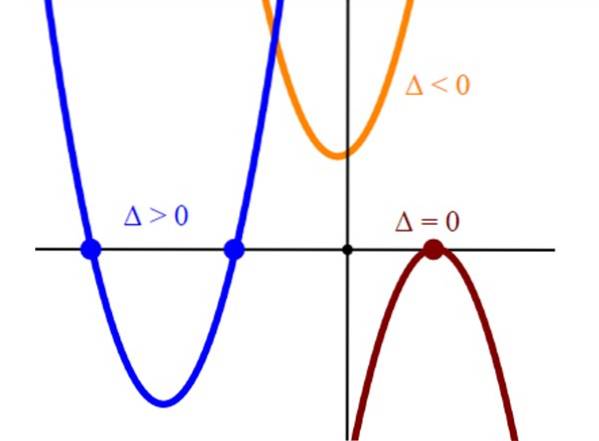
Røttene eller løsningene til den kvadratiske ligningen tilsvarer skjæringspunktet mellom parabolen y = øks^to + bx + c med den horisontale aksen eller x-aksen. Så når vi tegner graf for den tilsvarende parabolen, vil vi finne løsningen på den kvadratiske ligningen ved å lage y = 0.

Kuttene av parabolene med den horisontale aksen representerer løsningene i ligningen øks^to + bx + c = 0. En parabel som bare skjærer den horisontale aksen på et enkelt punkt har en enkelt rot, og dette vil alltid være toppunktet til parabolen.

Og til slutt, hvis en parabel ikke kutter den horisontale aksen, den tilsvarende ligningen øks^to + bx + c = 0 mangler reelle løsninger.

Å bygge en graf for hånd kan være arbeidskrevende, men med bruk av programmer som grafer på nettet er det veldig enkelt.

Oppløsning med vitenskapelig kalkulator

Mange modeller av vitenskapelige kalkulatorer har muligheten til å løse kvadratiske ligninger (og andre typer ligninger også). For å finne ut av det, må du sjekke menyen.

Når den kvadratiske ligningen til ett ukjent alternativ er valgt, ber menyen om å angi verdiene til koeffisientene a, b og c og returnerer de virkelige løsningene hvis de eksisterer. Og det er også modeller av vitenskapelige kalkulatorer som jobber med komplekse tall og tilbyr disse løsningene.

Diskriminant av en kvadratisk ligning

For å finne ut om ligningen har reelle løsninger eller ikke, og hvor mange det er, uten å måtte løse først, er diskriminanten Δ definert som mengden under kvadratroten:

Δ = b^to - 4ac

I henhold til diskriminantens tegn er det kjent hvor mange løsninger ligningen har i henhold til dette kriteriet:

-To virkelige løsninger: Δ> 0

-En ekte løsning (eller to identiske løsninger): Δ = 0

-Ingen reell løsning: Δ  < 0

For eksempel hvor mange løsninger gjør den kvadratiske ligningen -7x^to +12x + 64 = 0? Vi identifiserer koeffisientene:

a = -7

b = 12

c = 64

Δ = b^to - 4ac = 12^to - 4x (-7) x 64 = 144 + 1792 = 1936> 0

Ligningen har to løsninger. La oss nå se den andre:

x^to - 6x + 9 = 0

a = 1

b = -6

c = 9

Δ = (-6)^to - 4 x 1 x 9 = 36 - 36 = 0

Dette er en ligning med en enkelt løsning eller med to like løsninger.

Eksempler på enkle kvadratiske ligninger

I begynnelsen sa vi at ligninger av andre grad kunne være komplette hvis trinomialet er, og ufullstendig hvis den lineære termen eller den uavhengige termen manglet. La oss nå se på noen spesielle typer:

Ligning av skjemaet x^to + mx + n = 0

I dette tilfellet a = 1 og formelen reduseres til:

For denne typen ligning, og alltid avhengig av gjenværende koeffisienter, kan factoring-metoden fungere bra, som vi så i forrige avsnitt.

Ufullstendig ligning av skjemaøksen^to + c = 0

Løsningen, hvis den eksisterer, har formen:

Det er en reell løsning når a eller c har et negativt tegn, men hvis de to begrepene har samme tegn, vil løsningen være tenkt.

Ufullstendig ligning av skjemaet øks^to + bx = 0

Denne ligningen løses raskt ved hjelp av factoring, siden x er en vanlig faktor i begge termer. En av løsningene er alltid x = 0, den andre finnes slik:

øks^to + bx = 0

x (ax + b) = 0

ax + b = 0 → x = -b / a

La oss se et eksempel nedenfor. Finne ut av:

x^to - 5x = 0

x (x - 5) = 0

Derfor x₁ = 0 og x_to = 5

Ligninger med nevner

Det er forskjellige ligninger av en rasjonell type, der det ukjente kan være tilstede både i telleren og i nevneren, eller til og med bare i sistnevnte, og som ved hjelp av algebraiske manipulasjoner reduseres til kvadratiske ligninger.

Måten å løse dem på er å multiplisere begge sider av likheten med minst felles multiplum eller m.c.m av nevnerne og deretter omorganisere vilkårene. For eksempel:

Ligninger med høyere ordre som blir kvadratiske

Det er ligninger av høyere orden som kan løses som om de var kvadratiske ved hjelp av en endring av variabelen, for eksempel denne ligningen bi-firkant:

x⁴ - 10x^to + 9 = 0

La x^to = u, så blir ligningen:

eller^to - 10u + 9 = 0

Denne ligningen løses raskt ved å faktorisere, finne to tall som ble multiplisert til 9 og lagt til 10. Disse tallene er 9 og 1:

(u - 9). (u - 1) = 0

Derfor er løsningene i denne ligningen u₁ = 9 og u_to = 1. Nå returnerer vi endringen:

x^to = 9 → x₁ = 3 og x_to = -3

x^to = 1 → x₁ = 1 og x_to = -1

Den opprinnelige ligningen er av orden 4, derfor har den minst 4 røtter. Den i eksemplet er -3, -1, 1 og 3.

Enkle løste øvelser

- Øvelse 1

Løs følgende kvadratiske ligning med det ukjente i nevneren:

Det minst vanlige multiple er x (x + 2), og du må multiplisere alle vilkårene:

Tilsvarende uttrykk gjenstår:

5x (x + 2) - x = x (x + 2)

Vi utvikler:

5x^to + 10x - x = x^to + 2x

Alle vilkårene er transponert til venstre for likestillingen og til høyre forlater vi 0:

5x^to + 10x - x - x^to - 2x = 0

4x^to - 7x = 0

Vi faktor, siden det er en ufullstendig ligning:

x (4x - 7) = 0

En av løsningene er x = 0, den andre er:

4x = 7

x = 7/4

- Øvelse 2

Finn løsningen på kvadratiske ligninger:

a) -7x^to +12x + 64 = 0

b) x^to - 6x + 9 = 0

Løsning til

Fra denne ligningen kjenner vi determinanten Δ, fordi den ble beregnet som et eksempel før, så vi kommer til å dra nytte av den og uttrykke løsningsformelen slik:

x₁ = (-12 + 44) / -14 = - (32/14) = - (16/7)

x_to = (-12 - 44) / -14 = 4

Løsning b

Det firkantede trinomialet x^to - 6x + 9 er faktor, siden det er et perfekt kvadratisk trinomial:

x^to - 6x + 9 = (x-3)^to = 0

Løsningen på denne ligningen er x = 3.

- Øvelse 3

Hva er ligningen hvis løsninger er 3 og 4?

Løsning

Det fakturerte uttrykket er:

(x - 3) ⋅ (x - 4) = 0

Bruk av distribusjonseiendom:

x^to - 4x -3x + 12 = 0

De to sentrale begrepene er like og kan reduseres, og etterlater:

x^to - 7x + 12 = 0

Referanser

1. Baldor. 1977. Elementær algebra. Venezuelanske kulturutgaver.
2. Hoffman, J. Selection of Mathematics Topics. Volum 2.
3. Jiménez, R. 2008. Algebra. Prentice hall.
4. Stewart, J. 2006. Precalculus: Mathematics for Calculus. 5. Utgave. Cengage læring.
5. Zapata, F. 4 måter å løse en kvadratisk ligning på. Gjenopprettet fra: francesphysics.blogspot.com.
6. Zill, D. 1984. Algebra og trigonometri. Mcgraw hill.