
Homografisk funksjon hvordan man tegner graf, løste øvelser
De det funkethomografisk eller rasjonell ion Det er en type matematisk funksjon som består av inndelingen av to polynomkomponenter. Den adlyder skjemaet P (x) / Q (x), hvor Q (x) ikke kan ta en null form.
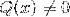
For eksempel tilsvarer uttrykket (2x - 1) / (x + 3) en homografisk funksjon med P (x) = 2x - 1 og Q (x) = x + 3.

De homografiske funksjonene utgjør en del av studien av de analytiske funksjonene, behandlet fra den grafiske tilnærmingen og fra studien av domenet og området. Dette skyldes begrensningene og begrunnelsen som må brukes for deres vedtak..
Artikkelindeks
- 1 Hva er en homografisk funksjon?
- 2 Blandet homografisk funksjon
- 2.1 Til og med den nte roten til den homografiske funksjonen
- 2.2 Logaritme for den homografiske funksjonen
- 3 Hvordan tegne en homografisk funksjon?
- 3.1 Røtter
- 3.2 Vertikal asymptote
- 3.3 Horisontal asymptote
- 3.4 Vekstintervall
- 3.5 Forfallintervall
- 3.6 Kryss med Y
- 4 Eksempler
- 4.1 Øvelse 1
- 4.2 Øvelse 1.2
- 5 Øvelse 2
- 6 Referanser
Hva er en homografisk funksjon?
De er rasjonelle uttrykk for en enkelt variabel, selv om dette ikke betyr at det ikke eksisterer et lignende uttrykk for to eller flere variabler, der det allerede ville være i nærvær av legemer i rommet som adlyder de samme mønstrene som den homografiske funksjonen i flyet.
De har reelle røtter i noen tilfeller, men eksistensen av vertikale og horisontale asymptoter opprettholdes alltid, så vel som intervaller for vekst og nedgang. Vanligvis er bare en av disse trendene til stede, men det er uttrykk som kan vise begge deler i utviklingen..
Domenet er begrenset av nevnerenes røtter, siden det ikke er noen divisjon med null av de reelle tallene.
Blandet homografisk funksjon
De er veldig hyppige i beregningen, spesielt differensielle og integrerte, som er nødvendige for å utlede og motvirke under bestemte formler. Noen av de vanligste klassifiseres nedenfor.
Selv nth roten til den homografiske funksjonen
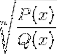
Ekskluder alle elementene fra domenet som gjør argumentet negativt. Røttene til stede i hvert polynomutbytteverdier på null når de blir evaluert.
Disse verdiene aksepteres av radikalen, selv om den grunnleggende begrensningen av den homografiske funksjonen må vurderes. Hvor Q (x) ikke kan motta nullverdier.
Løsningene til intervallene må avskjæres:
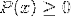
For å oppnå løsningen av kryssene kan skiltmetoden brukes blant andre.
Logaritme til den homografiske funksjonen
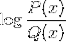
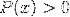
Det er også vanlig å finne begge uttrykkene i ett, blant andre mulige kombinasjoner.
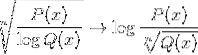
Hvordan tegne en homografisk funksjon?
Homografiske funksjoner samsvarer grafisk med hyperboler i planet. Som transporteres horisontalt og vertikalt i henhold til verdiene som definerer polynomene.
Det er flere elementer som vi må definere for å tegne en rasjonell eller homografisk funksjon.
Eiendom
Den første vil være røttene eller nullene til funksjonene P og Q.
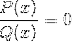
Verdiene som oppnås vil bli angitt på x-aksen i grafen. Angir skjæringspunktene i grafen med aksen.
Vertikal asymptote
De tilsvarer vertikale linjer, som avgrenser grafen i henhold til trendene som disse presenterer. De berører x-aksen ved verdiene som gjør nevneren null og vil aldri bli berørt av grafen til den homografiske funksjonen.
Horisontal asymptote
Representert av en horisontal sømlinje, avgrenser den en grense som funksjonen ikke vil bli definert for på det nøyaktige punktet. Trender vil bli observert før og etter denne linjen.
For å beregne det må vi ty til en metode som ligner på L'Hopitals metode, brukt til å løse grenser for rasjonelle funksjoner som har en tendens til uendelig. Vi må ta koeffisientene til de høyeste makter i teller og nevner av funksjonen.
For eksempel har følgende uttrykk en horisontal asymptote ved y = 2/1 = 2.
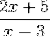
Vekstintervall
Ordinatverdiene vil ha trender merket på grafen på grunn av asymptotene. Ved vekst vil funksjonen øke i verdier når elementene i domenet blir evaluert fra venstre til høyre.
Reduser intervallet
Ordinatverdiene vil reduseres når domeneelementene evalueres fra venstre til høyre.
Hoppene som finnes i verdiene blir ikke tatt i betraktning når de øker eller synker. Dette skjer når grafen er nær en vertikal eller horisontal asymptote, hvor verdiene kan variere fra uendelig til negativ uendelig og omvendt..
Y kryss
Ved å sette verdien x til null, finner vi skjæringspunktet med ordinataksen. Dette er en veldig nyttig informasjon for å få grafen til den rasjonelle funksjonen.
Eksempler
Definer grafen for følgende uttrykk, finn røttene, vertikale og horisontale asymptoter, intervaller for vekst og reduksjon, og skjæringspunkt med ordinataksen.
Øvelse 1
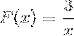
Uttrykket har ingen røtter, fordi det har en konstant verdi i telleren. Begrensningen for å søke vil være x forskjellig fra null. Med horisontal asymptote ved y = 0, og vertikal asymptote ved x = 0. Det er ingen skjæringspunkter med y-aksen.
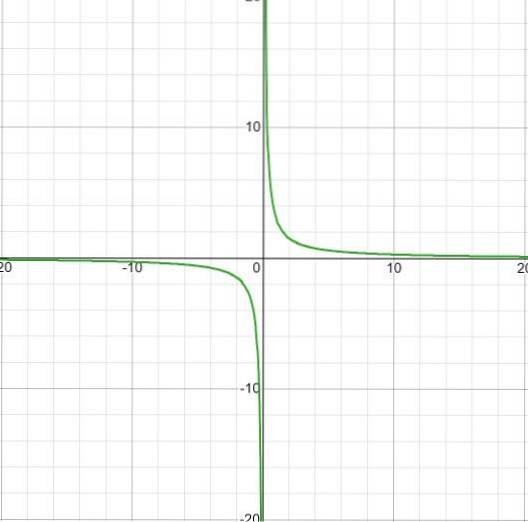
Det observeres at det ikke er noen vekstintervaller selv med hoppet fra minus til pluss uendelig ved x = 0.
Forfallintervallet er
ID: (-∞; o) U (0, ∞)
Øvelse 1.2
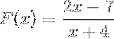
To polynomer observeres som i den opprinnelige definisjonen, så vi fortsetter i henhold til de etablerte trinnene.
Roten som er funnet er x = 7/2, som er resultatet av å sette funksjonen lik null.
Den vertikale asymptoten er ved x = - 4, som er verdien ekskludert fra domenet av den rasjonelle funksjonsbetingelsen.
Den horisontale asymptoten er ved y = 2, dette etter å ha delt 2/1, koeffisientene til variablene i grad 1.
Den har et y-skjæringspunkt = - 7/4. Verdien ble funnet etter å ha satt lik x til null.
Funksjonen vokser konstant, med et hopp fra pluss til minus uendelig rundt roten x = -4.
Dens vekstintervall er (-∞, - 4) U (- 4, ∞).
Når verdien av x nærmer seg uendelig, tar funksjonen verdier nær 2. Det samme skjer når x nærmer seg mer uendelig.
Uttrykket nærmer seg pluss uendelig når man vurderer til - 4 fra venstre, og til minus uendelig når man vurderer til - 4 fra høyre.
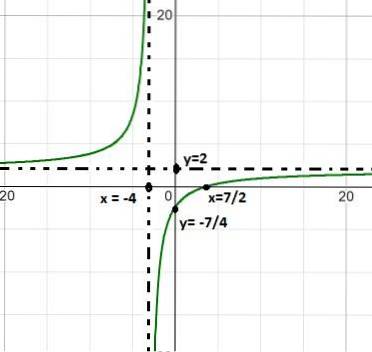
Øvelse 2
Grafen for følgende homografiske funksjon observeres:
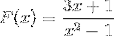
Beskriv dens oppførsel, røtter, vertikale og horisontale asymptoter, intervaller for vekst og reduksjon og skjæringspunkt med ordinataksen..
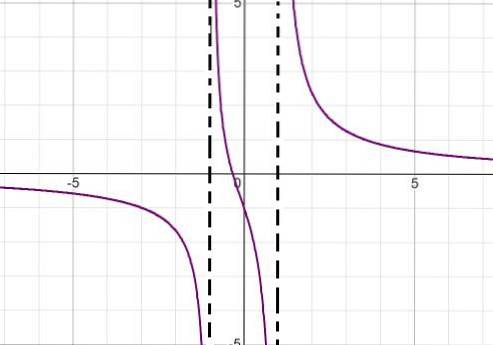
Nevneren til uttrykket forteller oss ved å faktorisere forskjellen i kvadrater (x + 1) (x - 1) verdiene til røttene. På denne måten kan begge vertikale asymptoter defineres som:
x = -1 og x = 1
Den horisontale asymptoten tilsvarer abscissa-aksen fordi den høyeste kraften er i nevneren.
Den eneste roten er definert av x = -1/3.
Uttrykket synker alltid fra venstre til høyre. Det nærmer seg null når det nærmer seg uendelig. Minus uendelig når du nærmer deg -1 fra venstre. Et pluss uendelig når det nærmer seg -1 fra høyre. Minus uendelig når du nærmer deg 1 fra venstre og mer uendelig når du nærmer deg 1 fra høyre.
Referanser
- Tilnærming med rasjonelle funksjoner. Donald J. Newman. American Mathematical Soc., 31. des. 1979
- Ortogonale rasjonelle funksjoner. UNIVERSIDAD DE LA LAGUNA TENERIFE ADHEMAR BULTHEEL, Adhemar Bultheel, Pablo Gonzalez-Vera, Erik Hendriksen, Olav Njastad. Cambridge University Press, 13. feb. 1999
- Rasjonell tilnærming av virkelige funksjoner. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3. mars. 2011
- Algebraiske funksjoner. Gilbert Ames Bliss. Courier Corporation, 1. jan 2004
- Journal of the Spanish Mathematical Society, bind 5-6. Spanish Mathematical Society, Madrid 1916



Ingen har kommentert denne artikkelen ennå.