
Ideell gassmodell, oppførsel, eksempler
EN ideell gass eller perfekt gass Det er en der den molekylære tiltrekningen eller frastøtningskraften mellom partiklene som komponerer den anses som ubetydelig, derfor er all dens indre energi kinetisk, det vil si energi assosiert med bevegelse.
I en slik gass er partiklene vanligvis ganske langt fra hverandre, selv om de fra tid til annen kolliderer med hverandre og med beholderens vegger..
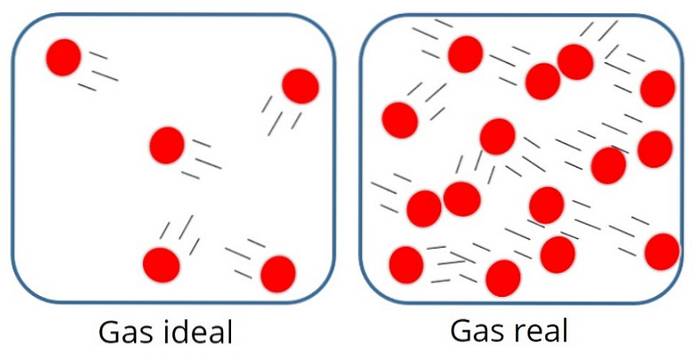
På den annen side, i den ideelle gassen, betyr ikke partikkelenes størrelse eller masse noe, siden det antas at volumet okkupert av dem er veldig lite sammenlignet med volumet av selve gassen..
Dette er selvfølgelig bare en tilnærming, for i realiteten er det alltid en viss grad av interaksjon mellom atomer og molekyler. Vi vet også at partikler opptar plass og har masse..
Imidlertid fungerer disse antagelsene ganske bra i mange tilfeller, for eksempel gasser med lav molekylvekt, i et godt trykk- og temperaturområde..
Gasser med høy molekylvekt, spesielt ved høyt trykk eller lave temperaturer, oppfører seg imidlertid ikke som idealgasser og andre modeller laget med det formål å beskrive dem med større presisjon..
Artikkelindeks
- 1 Første eksperimenter
- 1.1 De ideelle gasslovene
- 2 Ideell gassmodell
- 2.1 Ideell gassligning av tilstand
- 2.2 Gasskonstanten
- 3 Oppførsel av en ideell gass
- 4 Eksempler på ideelle gasser
- 4.1 Edelgasser
- 4.2 Luftballongen
- 4.3 Heliumballonger
- 5 Referanser
Første eksperimenter
Lovene som styrer gasser er empiriske, det vil si at de stammer fra eksperimentering. De mest bemerkelsesverdige eksperimentene ble utført gjennom det syttende, attende og tidlige nittende århundre.
Først er de av Robert Boyle (1627-1691) og Edme Mariotte (1620-1684), som uavhengig modifiserte Press i en gass og registrerte endringen av volum, å finne ut at de var omvendt proporsjonale: jo høyere trykk, jo mindre volum.

Jacques Charles (1746-1823) slo for sin del fast at volumet og temperatur absolutte verdier var direkte proporsjonale, så lenge trykket holdt seg konstant.
Amadeo Avogadro (1776-1856) oppdaget at to identiske volumer av forskjellige gasser inneholdt samme antall partikler, så lenge trykket og temperaturen var den samme. Og til slutt uttalte Joseph de Gay Lussac (1778-1850) at ved å holde volumet fast, er trykket i en gass direkte proporsjonalt med temperaturen..
De ideelle gasslover
Disse funnene kommer til uttrykk i enkle formler, kallende s til press, V til volum, n til antall partikler og T den ideelle gass temperaturen:
Boyle-Mariotte lov
Så lenge temperaturen er fast, skjer følgende:
p⋅V = konstant
Charles Law
Når gassen er under konstant trykk:
V / T = konstant
Gay Lussacs lov
Når du holder gassen på et fast volum, er det tilfreds med at:
p / T = konstant
Avogadros lov
Identiske volumer av gass, under samme trykk og temperaturforhold, har samme antall partikler. Derfor kan vi skrive:
V ∝ n
Hvor n er antall partikler og ∝ er symbolet på proporsjonalitet.
Ideell gassmodell
Den ideelle gassmodellen beskriver en gass slik at:
-Når partiklene samhandler, gjør de det i veldig kort tid ved hjelp av elastiske kollisjoner, der momentum og kinetisk energi er bevart..
-Dens bestanddeler er punktlige, med andre ord diameteren deres er mye mindre enn den gjennomsnittlige avstanden de reiser mellom en kollisjon og en annen..
-Intermolekylære krefter er ikke eksisterende.
-Kinetisk energi er proporsjonal med temperaturen.
Monatomiske gasser - hvis atomer ikke er bundet sammen - og lav molekylvekt, under standard betingelser for trykk og temperatur (atmosfæretrykk og 0 ° C temperatur), har slik oppførsel at den ideelle gassmodellen er en veldig god beskrivelse for dem..
Ideell gassligning av tilstand
Gasslovene som er oppført ovenfor, danner den generelle ligningen som styrer oppførselen til den ideelle gassen:
V ∝ n
V ∝ T
Derfor:
V ∝ n⋅T
Også fra Boyles lov:
V = konstant / s
Så vi kan bekrefte at:
V = (konstant x n⋅T) / p
Konstanten kalles gasskonstant og er betegnet med bokstaven R. Med dette valget relaterer den ideelle gassligningen for tilstand fire variabler som beskriver tilstanden til gassen, nemlig n, R, p og T, og etterlater:
p⋅V = n⋅R⋅T
Denne relativt enkle ligningen er i samsvar med de ideelle gasslovene. For eksempel, hvis temperaturen er konstant, reduseres ligningen til Boyle-Mariotte-loven.
Gasskonstanten
Som vi har sagt før, under standard betingelser for temperatur og trykk, det vil si ved 0 ° C (273,15 K) og en atmosfære av trykk, er oppførselen til mange gasser nær den for den ideelle gassen. Under disse forholdene er volumet på 1 mol av gassen 22.414 L.
I så fall:
R = (p⋅V) / (n⋅T) = (1 atm x 22,414 L) / (1 mol x 273,15 K) = 0,0821 atm ⋅ L / mol ⋅ K
Gasskonstanten kan også uttrykkes i andre enheter, for eksempel i SI International System er det verdt:
R = 8,314 J⋅ mol-1⋅ K-1
Når du løser et problem med den ideelle gassloven, er det praktisk å være oppmerksom på enhetene der konstanten uttrykkes, siden det er mange muligheter som vi kan se.
Oppførsel av en ideell gass
Som vi har sagt, oppfører seg enhver gass under standard betingelser for trykk og temperatur, og som har lav molekylvekt, veldig nær den ideelle gassen. Derfor er ligningen p⋅V = n⋅R⋅T anvendelig for å finne forholdet mellom de fire variablene som beskriver det: n, p, V og T.
På denne måten kan vi forestille oss en del ideell gass innelukket i en beholder og dannet av små partikler, som fra tid til annen kolliderer med hverandre og med beholderens vegger, alltid elastisk..
Dette er hva vi ser i den følgende animasjonen av en del helium, en monatomisk edelgass:
Eksempler på ideelle gasser
En ideell gass er en hypotetisk gass, det vil si at det er en idealisering, men i praksis oppfører mange gasser seg veldig nært, noe som gjør det mulig for modellen p⋅V = n⋅R arroT å gi veldig gode resultater..
Edelgasser
Eksempler på gasser som oppfører seg som ideelle under standardforhold er edelgasser, samt lette gasser: hydrogen, oksygen og nitrogen..
Den aerostatiske ballongen

Karls lov kan brukes på varmluftsballongen i figur 1: gassen varmes opp, derfor ekspanderer luften som fyller ballongen og som en konsekvens stiger den.
Heliumballonger
Helium er sammen med hydrogen det vanligste elementet i universet, og likevel er det sjeldent på jorden. Siden det er edelgass, er det inert, i motsetning til hydrogen, det er derfor heliumfylte ballonger er mye brukt som dekorative elementer..
Referanser
- Atkins, P. 1999. Fysisk kjemi. Omega-utgaver.
- Chang, R. 2013. Kjemi. 11. Utgave. Mc Graw Hill Utdanning.
- Cengel, Y. 2012. Termodynamikk. 7. utgave. Mcgraw hill.
- Cimbala, C. 2006. Fluid Mechanics, Fundamentals and Applications. Mc. Graw bakke.
- Giambattista, A. 2010. Fysikk. 2. plass. Ed. McGraw Hill.


Ingen har kommentert denne artikkelen ennå.