
Topp 9 kjennetegn ved rektangelet
De rektangel den er preget av å være en flat geometrisk figur som har fire sider og fire hjørner. Av disse fire sidene har det ene paret samme måling mens det andre paret har en måling som skiller seg fra det for det første paret..
Denne figuren er en polygon av parallellogramtypen, siden motsatte sider av et rektangel er parallelle og har de samme målene. Vinklene som utgjør rektanglene har en amplitude på 90 °, så de er rette vinkler. Det er her navnet kommer fra rektangel.

Det faktum at rektanglene har fire vinkler av samme amplitude får disse geometriske figurene til å kalles ekvivalenter.
Når et rektangel krysses av en diagonal linje, opprettes to trekanter. Krysser du et rektangel med to diagonale linjer, vil de krysse i midten av figuren.
9 nøkkelegenskaper om rektangler
1- Antall sider og dimensjon
Rektangler består av fire sider. Vi kan dele disse sidene i to par: et par sider måler det samme, mens det andre paret har målinger høyere eller lavere enn forrige par..
Motstridende sider har samme målinger, mens påfølgende sider har forskjellige målinger.
I tillegg til dette er rektanglene todimensjonale figurer, noe som betyr at de bare har to dimensjoner: bredde og høyde..
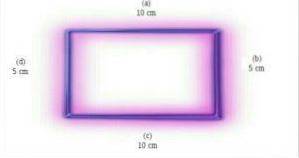
Den grunnleggende egenskapen til rektangler er at de har fire sider. Dette er todimensjonale figurer, fordi de er flate. Foto hentet fra en.wikipedia.org
2- Polygon
Rektanglene er en polygon. I denne forstand er rektangler geometriske figurer, som er avgrenset av en lukket polygonal linje (det vil si av et rett linjesegment som lukker seg inn på seg selv).
For å være mer spesifikk, er rektangler firsidige polygoner, fordi de har fire sider.
3- De er ikke ensidige polygoner
En polygon er ligesidig når alle sidene måler det samme. Sidene av et rektangel har ikke de samme målene. Av denne grunn kan det ikke sies at rektanglene er liksidige.
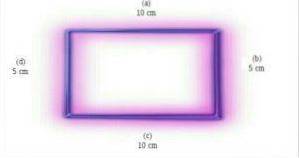
Rektangler er ikke like-sidige, fordi deres sider har forskjellige mål. På bildet over har sidene (a) og (c) den samme målingen, som skiller seg fra målingene på sidene (b) og (d). Foto hentet og tilpasset fra en.wikipedia.org
4- Ekvivalent polygon
Ekvivalent polygoner er de der de består av vinkler som har samme amplitude.
Alle rektangler består av fire rette vinkler (det vil si 90 ° vinkler). Et rektangel på 10 cm x 20 cm vil ha fire 90 ° vinkler, det samme vil skje med et rektangel av større eller mindre mål.
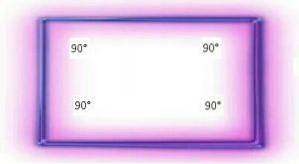
Alle rektangler er ekvivalenter fordi vinklene har samme amplitude. Det vil si 90 °. Foto hentet og tilpasset fra en.wikipedia.org
5- Området til et rektangel
Arealet til et rektangel er lik produktet av basen ganger høyden, basen er den horisontale siden mens høyden er den vertikale siden. En enklere måte å se på det er å multiplisere målingene på to sammenhengende sider.
Formelen for å beregne arealet til denne geometriske figuren er:
a = b x A
Noen eksempler på å beregne arealet til et rektangel er:
- Rektangel med en base på 5 cm og en høyde på 2 cm. 5cm x 2cm = 10cmto
- Rektangel med en base på 2 m og en høyde på 0,5 m. 2m x 0,5m = 2mto
- Rektangel med en base på 18 m og en høyde på 15 m. 18 m x 15 m = 270 mto
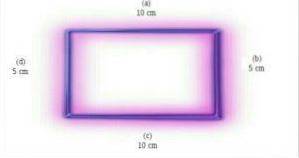
Rektangelet på bildet har en base på 10 cm og en høyde på 5 cm. Arealet vil være et produkt på 10 cm x 5 cm. I dette tilfellet er arealet på rektangelet 50 cmto. Foto hentet og tilpasset fra en.wikipedia.org
6- Rektangler er parallellogrammer
Kvadrilaterale kan klassifiseres i tre typer: trapeser, trapeser og parallellogrammer. Sistnevnte er preget av å ha to par parallelle sider, som ikke nødvendigvis trenger å ha de samme målene..
I denne forstand er rektanglene parallellogrammer, siden to par sider vender mot hverandre.
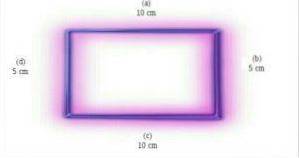
Rektangler er parallellogrammer fordi de har to par sider som er parallelle.. Sidene (a) og (c) er parallelle. Sidene (b) og (d) er parallelle. Foto hentet og tilpasset fra en.wikipedia.org
7- De motsatte vinklene er kongruente og de påfølgende er komplementære
De motsatte vinklene er de som er i de ikke-påfølgende hjørnene i figuren. Mens påfølgende vinkler er de som er tilstøtende, den ene ved siden av den andre.
To vinkler er kongruente når de har samme amplitude. For sin del er to vinkler komplementære når summen av amplituden deres gir en vinkel på 180 °, eller hva som er det samme, en rett vinkel.
Alle vinklene til et rektangel måler 90 °, så det kan sies at de motsatte vinklene til denne geometriske figuren er kongruente.
Med hensyn til påfølgende vinkler består rektangelet av 90 ° vinkler. Hvis de etterfølgende legges til, blir resultatet 180 °. Så det handler om komplementære vinkler.
8- Den er dannet av to høyre trekanter
Hvis en diagonal tegnes i rektangelet (en linje som går fra en vinkel på rektangelet til en annen som er motsatt), oppnås to høyre trekanter. Denne typen trekant er en som er dannet av en rett vinkel og to spisse vinkler.

På bildet representerer stinglinjen diagonalen. Dette deler rektangelet i to trekanter. Foto hentet og tilpasset fra en.wikipedia.org
9- Diagonalene krysser hverandre ved midtpunktet
Som allerede forklart er diagonalene linjene som går fra en av vinklene til en annen motsatt vinkel. Hvis to diagonaler er tegnet i rektangelet, vil de krysses ved midtpunktet på figuren.
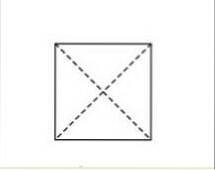
De stiplede linjene representerer diagonalene. Disse linjene krysser nøyaktig midt i rektangelet. Foto hentet og tilpasset fra dummies.com
Referanser
- Rektangel. Hentet 24. juli 2017 fra mathisfun.com.
- Rektangel. Hentet 24. juli 2017 fra merriam-webster.com.
- Egenskaper til romber, rektangler og firkanter. Hentet 24. juli 2017 fra dummies.com.
- Rektangel. Hentet 24. juli 2017 fra en.wikipedia.org.
- Rektangel. Hentet 24. juli 2017 fra collinsdictionary.com.
- Grunnleggende geometriske former. Hentet 24. juli 2017 fra universalclass.com.
- Quadrilaterals. Hentet 24. juli 2017 fra mathisfun.coma.



Ingen har kommentert denne artikkelen ennå.