
Faradays lovformel, enheter, eksperimenter, øvelse,
De Faradays lov i elektromagnetisme sier at en skiftende magnetfeltstrøm er i stand til å indusere en elektrisk strøm i en lukket krets.
I 1831 eksperimenterte den engelske fysikeren Michael Faraday med bevegelige ledere innenfor et magnetfelt og også varierende magnetfelt som passerte gjennom faste ledere..
Faraday innså at hvis han varierte magnetfeltstrømmen over tid, var han i stand til å etablere en spenning proporsjonal med den variasjonen. Hvis ε er spenningen eller indusert elektromotorisk kraft (indusert emf) og Φ er magnetfeltstrømmen, kan den i matematisk form uttrykkes:
| ε | = ΔΦ / Δt
Der symbolet Δ indikerer variasjon av mengden og stolpene i emf indikerer den absolutte verdien av dette. Siden det er en lukket krets, kan strømmen strømme i en retning eller den andre.
Magnetisk strømning, produsert av et magnetfelt over en overflate, kan variere på flere måter, for eksempel:
-Å bevege en stangmagnet gjennom en sirkulær sløyfe.
-Øker eller reduserer intensiteten til magnetfeltet som passerer gjennom løkken.
-Å la feltet stå fast, men ved hjelp av en eller annen mekanisme endre området på sløyfen.
-Kombinere metodene ovenfor.

Artikkelindeks
- 1 Formler og enheter
- 1.1 Lenzs lov
- 2 Faraday eksperimenter
- 2.1 Variasjon av magnetisk strømning ved rotasjon
- 3 Referanser
Formler og enheter
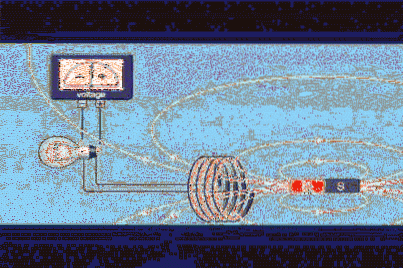
Anta at du har en lukket krets av område A, for eksempel en sirkulær sløyfe eller vikling lik den i figur 1, og at du har en magnet som produserer et magnetfelt B.
Magnetfeltstrømmen Φ er en skalar størrelse som refererer til antall feltlinjer som krysser område A. I figur 1 er de hvite linjene som forlater magnetens nordpol og går tilbake gjennom sør.
Feltets intensitet vil være proporsjonal med antall linjer per arealeenhet, så vi kan se at det er veldig intenst ved polene. Men vi kan ha et veldig intenst felt som ikke gir strøm i sløyfen, noe vi kan oppnå ved å endre orienteringen til denne (eller magneten).
For å ta hensyn til orienteringsfaktoren er magnetfeltstrømmen definert som det skalære produktet mellom B Y n, å være n enhetens normale vektor til overflaten av sløyfen og som indikerer orienteringen:
Φ = B•n A = BA.cosθ
Hvor θ er vinkelen mellom B Y n. Hvis for eksempel B Y n er vinkelrett, magnetfeltstrømmen er null, for i så fall er feltet tangent til sløyfens plan og kan ikke passere gjennom overflaten.
I stedet for ja B Y n er parallelle, betyr det at feltet er vinkelrett på sløyfens plan og linjene passerer gjennom det så langt som mulig.
Enheten i det internasjonale systemet for F er weberen (W), hvor 1 W = 1 T.mto (les "tesla per kvadratmeter").
Lenzs lov
I figur 1 kan vi se at polariteten til spenningen endres når magneten beveger seg. Polariteten er etablert av Lenzs lov, som sier at den induserte spenningen må motsette seg variasjonen som produserer den.
Hvis for eksempel magnetfluksen som produseres av magneten øker, etableres en strøm i lederen som sirkulerer og skaper sin egen strøm, som motsetter seg denne økningen..
Hvis tvert imot, strømmen som oppstår av magneten, synker, sirkulerer den induserte strømmen på en slik måte at dens egen strøm motvirker nevnte reduksjon..
For å ta hensyn til dette fenomenet settes et negativt tegn foran Faradays lov, og det er ikke lenger nødvendig å plassere de absolutte verdifeltene:
ε = -ΔΦ / At
Dette er Faraday-Lenz-loven. Hvis flytvariasjonen er uendelig liten, erstattes deltas med differensialer:
ε = -dΦ / dt
Ovennevnte ligning er gyldig for en sløyfe. Men hvis vi har en spole med N-svinger, er resultatet mye bedre, fordi emf multipliseres N ganger:
ε = - N (dΦ / dt)
Faraday eksperimenter
For at strømmen skal slå på pæren som skal produseres, må det være relativ bevegelse mellom magneten og sløyfen. Dette er en av måtene fluksen kan variere på, fordi på denne måten endres intensiteten til feltet som går gjennom sløyfen..
Så snart magnetens bevegelse opphører, slukker pæren, selv om magneten står stille midt i løkken. Det som trengs for å sirkulere strømmen som slår på pæren, er at feltstrømmen varierer.
Når magnetfeltet varierer med tiden, kan vi uttrykke det som:
B = B (t).
Ved å holde området A på sløyfen konstant og la den være fast i en konstant vinkel, som i tilfelle av figuren er 0º, så:


Hvis det er mulig å endre sløyfeområdet, la orienteringen være fast og plassere den midt i et konstant felt, blir den induserte emk gitt av:

En måte å oppnå dette på er å sette en stang som glir på en lederskinne med en viss hastighet, som vist i følgende figur.

Stangen og skinnen, pluss en lyspære eller en motstand forbundet med ledende ledninger, danner en lukket krets i form av en rektangulær sløyfe..
Når du skyver stangen, lengden x øker eller avtar, og med det endres området på sløyfen, noe som er nok til å skape en variabel flyt.
Variasjon av magnetisk strømning ved rotasjon
Som vi sa før, hvis vinkelen mellom B og sløyfens normale endres, feltstrømmen endres i henhold til:
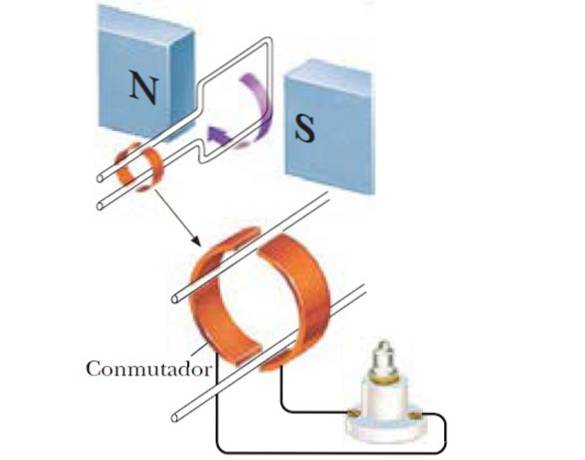

Dermed oppnås en sinusformet generator, og hvis det i stedet for en enkelt spole brukes et antall N spoler, er den induserte emf større:


En sirkulær N-spole og radius R, roterer med vinkelfrekvensen ω midt i et magnetfelt av størrelse B. Finn et uttrykk for maksimal emf indusert i spolen.
Løsning
Uttrykket for emk indusert av rotasjon brukes når spolen har N svinger, vel vitende om at:
-Arealet av spolen er A = πRto
-Vinkelen θ varierer som en funksjon av tiden som θ = ωt
Det er viktig å merke seg at først θ = ω er erstattet i Faradays lov og snart er avledet med hensyn til tid:
ε = -NBA (cos θ) '= -NB (πRto[cos (ωt)] '= NBω (πRto) synd (ωt)
Siden maksimal emf blir bedt om, oppstår det når sin ωt = 1, så til slutt:
εmaks = NBω (πRto)
Referanser
- Figueroa, D. 2005. Serie: Physics for Sciences and Engineering. Volum 6. Elektromagnetisme. Redigert av Douglas Figueroa (USB).
- Giambattista, A. 2010. Fysikk. Andre utgave. Mcgraw hill.
- Giancoli, D. 2006. Fysikk: prinsipper med applikasjoner. Sjette. Ed. Prentice Hall.
- Resnick, R. 1999. Fysikk. Vol. 2. 3. utgave på spansk. Compañía Editorial Continental S.A. av C.V.
- Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Red. Bind 2.



Ingen har kommentert denne artikkelen ennå.