De Hookes lov påpeker at deformasjonen en elastisk gjenstand opplever er direkte proporsjonal med kraften som påføres den. Konstanten av proporsjonaliteten avhenger av gjenstandens natur, dens geometri og materialet den er laget med..
Alle materialer har elastiske egenskaper i større eller mindre grad, så de overholder Hookes lov så lenge de går tilbake til sine opprinnelige dimensjoner, når kraften opphører. Fjærer og strikker er gode eksempler på gjenstander som oppfyller Hookes lov, men det er også stålpinner som er en del av en bro.
Å ta en fjær eller fjær som et eksempel, for å holde den strukket eller komprimert, er det nødvendig å påføre en kraft hvis størrelse er F. I følge Hookes lov vil fjæren oppleve en deformasjon x:
F ∝ x
Konstanten av proporsjonalitet, som å være en kilde kalles vårstivhet konstant, betegnes som k, derfor:
F = k⋅x
I enhetene til det internasjonale systemet er styrken i newton (N) og deformasjonen i meter (m). Derfor har vårkonstanten enheter på N / m. Fjærkonstanten representerer kraften som må påføres for å deformere den med 1 m lengde.
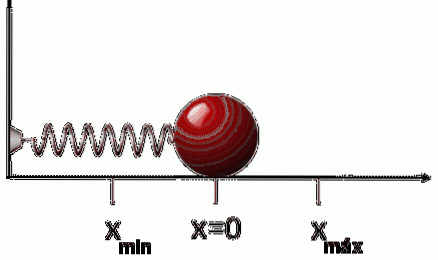
Hvis den frigjøres etter å ha strukket eller komprimert fjæren, vil den bevege seg i motsatt retning av den påførte kraften. Dette betyr at hvis vi strekker den, komprimerer den og omvendt. Derav styrken FR hva våren anstrenger Det er:
FR = -k⋅x
Det negative tegnet indikerer det ovennevnte: at styrken motarbeider forskyvning, derfor er denne kraften kjent som gjenopprettende kraft.
Artikkelindeks
Forholdet mellom styrke og forskyvning på en vår ble oppdaget av Robert Hooke (1635-1703), en bemerkelsesverdig engelsk fysiker kjent for sin rivalisering med Isaac Newton. Hooke var en allsidig forsker som vellykket våget seg inn i forskjellige vitenskapsfelt: mekanikk, biologi, astronomi og arkitektur..
Hooke innså at hvis kraften som påføres en fjær ikke er veldig stor, deformeres fjæren proporsjonalt med kraften, og når kraften forsvinner, går fjæren tilbake til sin naturlige lengde.
Dermed er Hookes lov i grafisk form i form av en rett linje, hvor skråningen er vårkonstant. Følgende bilde viser kraften som utøves på fjæren for å strekke den - eller komprimere den - som en funksjon av posisjon x. Legg også merke til at kraften ikke avhenger av vårens naturlige lengde, men av dens forskyvning..
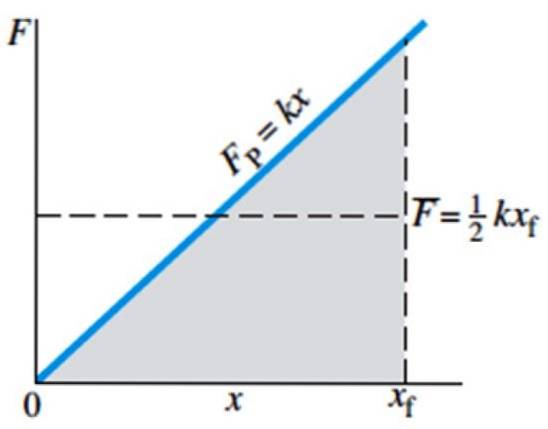
Gjennomsnittlig kraft er indikert på grafen med stolpen F og er lik ½ kxF, hvor xF er vårens endelige posisjon.
Både kraften som utøves på fjæren, og kraften den utøver på en gjenstand som er bundet til den, er variable krefter. Jo mer du vil strekke eller komprimere våren, jo mer kraft må du bruke for å oppnå den..
Når en deformerende kraft påføres fjæren, utføres arbeid som er lagret på våren og kan brukes senere..
Mekanisk arbeid er definert som området under grafen for kraft F som en funksjon av posisjon x. For å beregne arbeidet W som en variabel kraft F (x) gjør når et objekt flyttes fra posisjon x1 opp til posisjon xto vi må beregne den bestemte integralen:
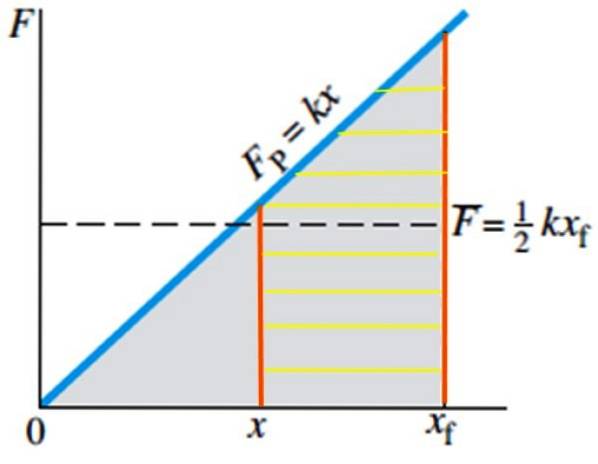
Når det gjelder arbeidet som kreves for å bringe en fjær fra sin likevektsposisjon til posisjon xF Det er veldig enkelt, siden området som skal beregnes, er det i trekanten som er skyggelagt i grått i figur 4, hvis formel er kjent:
Areal av trekanten = ½ base. høyde
Derfor er det nødvendige arbeidet:
W = ½ xF . (kxF) = ½ k (xF)to
Og hvis du vil beregne arbeidet som er nødvendig for å bringe fjæren fra posisjon x til posisjon xF, ville være ekvivalent med å beregne arealet til den klekkede trapesformen i figur 5:
W = ½ k (xF)to - ½ k xto
Avhengig av applikasjonen de er ment for, kan fjærene være spiralformede, sylindriske, koniske, spiralformede, med et sirkulært tverrsnitt (den vanligste), firkantede eller rektangulære..
En mye brukt klassifisering er i henhold til hvilken type innsats de skal utsettes for: det er vridnings-, bøynings-, kompresjons- og forlengelsesfjærer. Sistnevnte brukes mye, og noen fungerer likt for spenning og komprimering..
Et eksempel på en trykkfjær er den som brukes i leketøyet pogo eller hoppestokk. Disse fjærene lagrer mye potensiell energi når de komprimeres og frigjør den litt etter litt når de går tilbake til likevektsposisjonen. På denne måten er ikke reboundene for brå.
Trampolinfjærer er forlengelsesfjærtypen og er produsert med tett viklede spoler, med to kroker i endene. De er i stand til å beholde mye potensiell energi, som de deretter frigjør når noen klatrer opp og begynner å hoppe på matten, som også har sin egen elastiske respons, som alle materialer..
Torsjonsfjærer er veldig vanlige, fordi de brukes til å lage klesnåler. I stedet for kroker i endene, bøyer de seg i en vinkel for å motstå torsjonskrefter.
De mest egnede materialene for å lage fjærer er de med en ultimate motstand (endelig motstand) høy, det vil si at de støtter en stor innsats før de bryter. Det er også ønskelig at materialet har et høyt flytepunkt, slik at det ikke mister sine elastiske egenskaper med liten innsats..
Kraftige fjærer er laget av legeringer, inkludert høykarbonstål, kobber, nikkel og bronse.
Siden fjærer har dyden til å lagre potensiell energi når de strekkes eller komprimeres, er de i stand til å gjøre arbeid ved å flytte ting som mekanismer..
På denne måten har fjærene mange bruksområder, fra små og hverdagslige gjenstander, gjennom biler, til maskiner av alle slag. Fjærene er vant til å:
-Fukt vibrasjoner.
-Produsere uttrekkbare mekanismer: penner, klesklyper, hårklipp.
-Lag vårvekter eller dynamometre
Og de er også en del av mekanismen for:
-Klokker.
-Trampoliner.
-Låser.
-Leker.
-Våpen.
-Nålemålere, for eksempel galvanometeret, brukes til å måle strømmer, spenninger og motstand.
En kraft på 5,0 N påføres en fjær, noe som fører til at en lengde på 3,5 cm strekkes fra sin naturlige lengde..
a) Hvor mye strekker den seg når den påførte kraften er 7 N?
b) Finn arbeidet som er utført av den påførte kraften for å strekke fjæren 3,5 cm fra sin naturlige lengde.
Å vite at fjæren strekkes 3,5 cm ved å bruke 5,0 N, kan vi beregne dens konstant:
k = F / x = 5,0 N / 3,5 cm = 1,43 N / cm.
Når en kraft på 7 N påføres, oppnås følgende strekk:
x = F / k = 7,0 N / 1,43 N / m = 4,9 cm
Arbeidet som kreves for å deformere en fjær er gitt av:
W = ½ kxto = 0,5 x 1,43 N / cm x (3,5 cm)to = 8,76 N. cm = 8,76 N. 1 x 10 -to m = 0,0876 J.
En fjær med ubetydelig masse og 10 cm lang er hengt opp fra en støtte. Hvis det henges en masse på 2 kg, strekkes våren til 15 cm. Regne ut:
a) Vårkonstanten
b) Fjærens størrelse når en 3 kg masse er suspendert.
Vårstrekningen er x = 15 - 10 cm = 5 cm
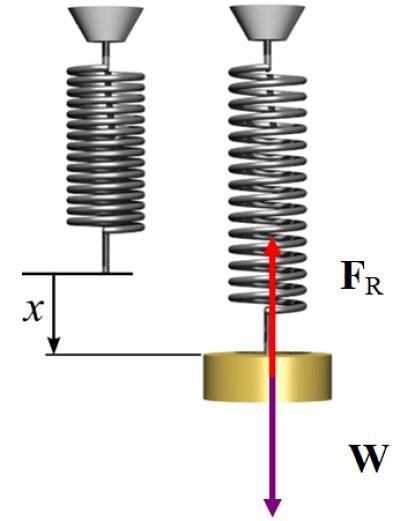
Siden systemet er i statisk likevekt, styres kraften som fjæren utøver når det strekkes, loddrett oppover for å kompensere for vekten som er rettet nedover, og deretter:
FR = W → kx = mg
k = 2 x 9,8 N / 5 x 10 -to m = 392 N / m
Når en vekt på 3 kg er suspendert, er den nye kraften W = 3 x 9,8 N = 29,4 N
I et slikt tilfelle er strekningen:
x = mg / k = 29. 4 N / 392 N / m = 0,075 m = 7,5 cm
Ingen har kommentert denne artikkelen ennå.