Blokkere algebraelementer, eksempler, løste øvelser

De blokker algebra refererer til settet med operasjoner som utføres gjennom blokker. Disse og noen andre elementer tjener til å skjematisk representere et system og enkelt visualisere dets respons på en gitt inngang..

Generelt inneholder et system forskjellige elektriske, elektroniske og elektromekaniske elementer, og hver av dem, med sin respektive funksjon og posisjon i systemet, samt måten de er relatert til, er skissert gjennom funksjonelle blokker.

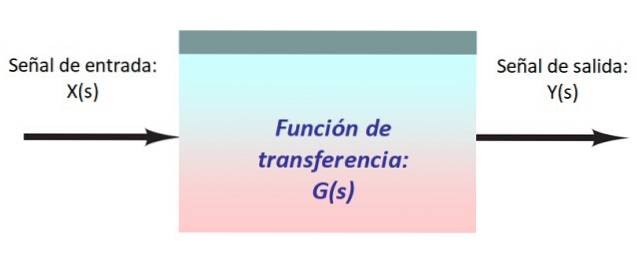
I figuren ovenfor er det et veldig enkelt system, bestående av et inngangssignal X (er), som kommer inn i blokken med overføringsfunksjonen G (s) som modifiserer den og produserer utgangen Y (s).

Det er praktisk å representere signalene og deres vei gjennom systemet ved hjelp av piler som går inn og ut av hver blokk. Vanligvis blir signalstrømmen dirigert fra venstre mot høyre.

Fordelen med denne typen skjematisk er den visuelle hjelpen den gir for å forstå systemet, selv om det ikke er en fysisk representasjon av systemet. Faktisk er blokkdiagrammet ikke unikt, for avhengig av synspunktet kan flere diagrammer av det samme systemet til og med tegnes..

Det kan også skje at det samme diagrammet betjener flere systemer som ikke nødvendigvis er relatert til hverandre, så lenge det tilstrekkelig beskriver deres atferd. Det er forskjellige systemer hvis respons er lik i mange henseender, for eksempel en LC-krets (induktorkondensator) og et massefjærsystem..

Artikkelindeks

• 1 Hva er et blokkdiagram?
• 2 Elementer av blokkdiagrammet
  • 2.1 Signalet
  • 2.2 Blokken
  • 2.3 Sumpoeng
  • 2.4 Grenpunkt
• 3 Eksempler på blokkalgebraregler
  • 3.1 Kaskader
  • 3.2 Blokker parallelt
  • 3.3 Flytt en adder til venstre
  • 3.4 Flytt en adder til høyre
  • 3.5 Flytte et forgreningspunkt fra venstre til høyre
  • 3.6 Flytt et forgreningspunkt fra høyre til venstre
  • 3.7 Tilbakemeldingssystem
  • 3.8 System med tilbakemelding og svinger
• 4 Løst øvelser
  • 4.1 Øvelse 1
  • 4.2 Øvelse 2
• 5 Referanser

Hva er et blokkdiagram?

Systemene er generelt mer kompliserte enn den i figur 1, men blokkalgebra gir en rekke enkle regler for å manipulere systemskjemaet og redusere det til sin enkleste versjon..

Som forklart i begynnelsen, bruker diagrammet blokker, piler og sirkler for å etablere forholdet mellom hver komponent i systemet og strømmen av signaler som går gjennom det..

Blokk algebra lar deg sammenligne to eller flere signaler ved å legge til, trekke fra og multiplisere dem, samt analysere bidraget som hver komponent gir til systemet.

Takket være dette er det mulig å redusere hele systemet til et enkelt inngangssignal, en enkelt overføringsfunksjon som fullt ut beskriver systemets handling og den tilsvarende utgangen..

Blokkdiagramelementer

Elementene i blokkdiagrammet er som følger:

Signalet

Signalene er av veldig variert natur, for eksempel er det vanlig at det er en elektrisk strøm eller en spenning, men det kan være lys, lyd og mer. Det viktige er at den inneholder informasjon om et bestemt system.

Signalet er betegnet med en stor bokstav hvis det er en funksjon av variabelen s av Laplace-transformasjonen: X (s) (se figur 1) eller med små bokstaver hvis det er en funksjon av tiden t, som x (t).

I blokkdiagrammet er inngangssignalet representert av en pil rettet mot blokken, mens utgangssignalet, betegnet som Y (s) eller y (t), er indikert med en utgående pil.

Både inngangs- og utgangssignalene er unike, og retningen informasjonen flyter bestemmes av pilens retning. Og algebraen er den samme for en av de to variablene.

Blokken

Blokken er representert med et kvadrat eller et rektangel (se figur 1) og kan brukes til å utføre operasjoner eller implementere overføringsfunksjonen, som vanligvis betegnes med stor bokstav G. Denne funksjonen er en matematisk modell som bruker svaret tilbys av systemet til et inngangssignal.

Overføringsfunksjonen kan uttrykkes i form av tid t som G (t) eller variabelen s som G (s).

Når inngangssignalet X (er) når blokken, multipliseres det med overføringsfunksjonen og transformeres til utgangssignalet Y (s). Matematisk uttrykkes det slik:

Y (s) = X (s). G (s)

Tilsvarende er overføringsfunksjonen forholdet mellom Laplace-transformasjonen av utgangssignalet og Laplace-transformasjonen av inngangssignalet, forutsatt at de innledende forholdene til systemet er null:

G (s) = Y (s) / X (s)

Sum poeng

Tilleggspunktet, eller addereren, er symbolisert av en sirkel med et kryss inni. Den brukes til å kombinere to eller flere signaler ved hjelp av addisjon og subtraksjon. På slutten av pilen som symboliserer tegnet, plasseres et + tegn direkte hvis tegnet legges til eller et - tegn hvis det trekkes fra..

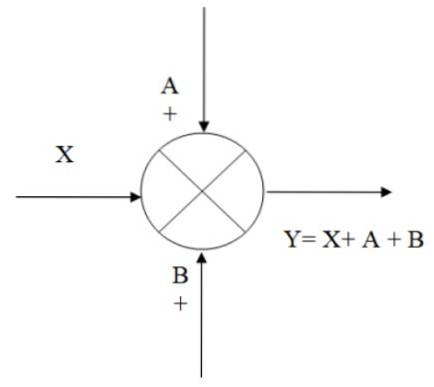
I den følgende figuren er det et eksempel på hvordan addereren fungerer: vi har inngangssignalet X, som signalene A og B er lagt til, og får resultatet Y, som er algebraisk ekvivalent med:

Y = X + A + B

Grenpunkt

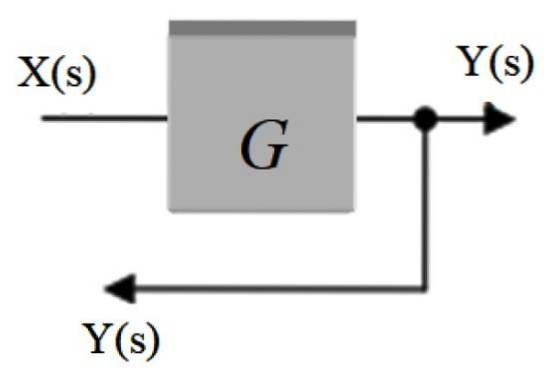
Det kalles også forgreningspunkt. I den distribueres signalet som kommer ut av en blokk til andre blokker eller til en hugger. Den er representert av et punkt plassert på signalpilen, og en annen pil kommer ut av den som omdirigerer signalet til en annen del.

Eksempler på blokkalgebraregler

Som forklart tidligere, er ideen å uttrykke systemet ved hjelp av blokkdiagrammet og redusere det for å finne overføringsfunksjonen som beskriver det. Følgende er blokkalgebrareglene for å forenkle diagrammer:

Cascading blokker

Når du har et signal som går suksessivt gjennom G-blokkene₁, G_to, G₃..., reduseres til en enkelt blokk hvis overføringsfunksjon er produktet av G₁, G_to, G₃...

I det følgende eksemplet kommer signalet X (e) inn i den første blokken, og utgangen er:

Y₁(s) = X (s) .G₁(s)

Snu Y₁(s) gå inn i blokk G_to(s), hvis produksjon er:

Y_to(s) = X (s) .G₁(s). G_to(s)

Fremgangsmåten er gyldig for n kaskadeblokker:

Y_n (s) = X (s). G₁(s) .G_to(s) ... G_n(s)

Parallelle blokker

I diagrammet til venstre forgrener signalet X seg for å komme inn i G-blokkene₁(s) og G_to(s):

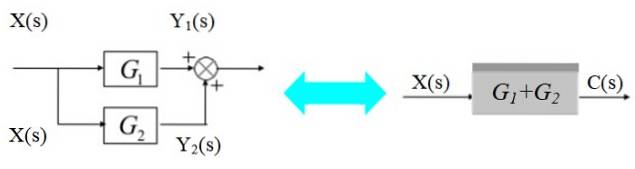
De respektive utgangssignalene er:

Y₁(s) = X (s) .G₁(s)

Y_to(s) = X (s) .G_to(s)

Disse signalene legges sammen for å oppnå:

C (s) = Y₁(s) + Y_to(s) = X (s). [G₁(s) + G_to(s)]

Som vist i diagrammet til høyre.

Flytt en hugger til venstre

En hugger kan flyttes til venstre for blokken som følger:

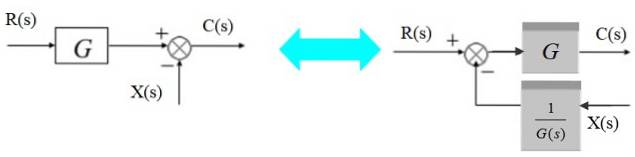
Til venstre er utgangssignalet:

C (s) = R (s). G (s) - X (s)

Tilsvarende til høyre:

C (s) = [R (s) - X (s) / G (s)]. G (s)

Flytt en hugger til høyre

Adderingen kan flyttes til høyre for blokken slik:

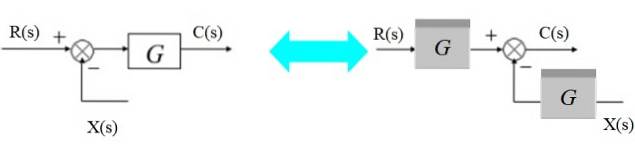
Til venstre har vi: [R (s) - X (s)]. G (s) = C (s)

Og til høyre:

R (s). G (s) - X (s). G (s) = C (s)

Flytt et forgreningspunkt fra venstre til høyre

For å flytte forgreningspunktet fra venstre til høyre for blokken, må du bare observere at utgangen C (s) til høyre er produktet X (s) .G (s). Siden du vil konvertere den til X (s) igjen, multipliser med inversen av G (s).

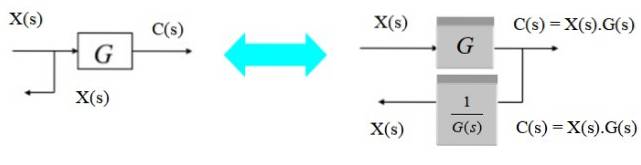
Flytt et forgreningspunkt fra høyre til venstre

Alternativt kan forgreningspunktet flyttes fra høyre til venstre som følger:

Siden vi ved utgangen av grenen vil oppnå C (s), setter du ganske enkelt inn en ny blokk G (s) ved et forgreningspunkt til venstre for den opprinnelige blokken.

Tilbakemeldingssystem

I det følgende systemet blir utgangssignalet C (s) matet tilbake gjennom huggeren til venstre:

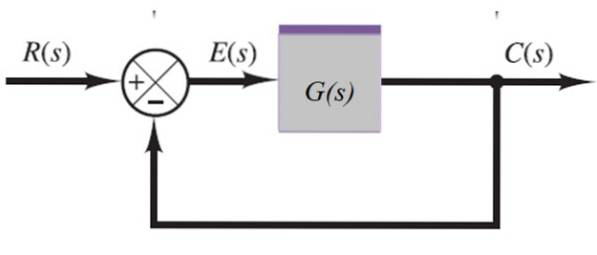
C (s) = E (s). G (s)

Men:

E (s) = R (s) -C (s)

Ved å erstatte dette uttrykket i forrige ligning forblir det: C (s) = [R (s) -C (s)]. G (s), hvor C (s) kan løses:

C (s) + C (s) .G (s) = R (s) .G (s) → C (s). [1 + G (s)] = R (s) .G (s)

C (s) = R (s). G (s) / [1 + G (s)]

Eller alternativt:

C (s) / R (s) = G (s) / [1 + G (s)]

I grafisk form forblir det etter forenkling:

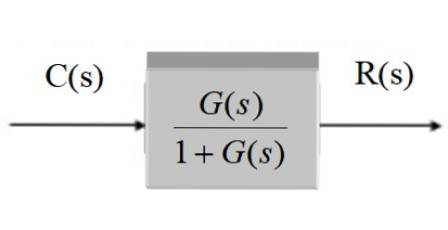
System med tilbakemelding og svinger

Transduseren består av overføringsfunksjonen H (s):

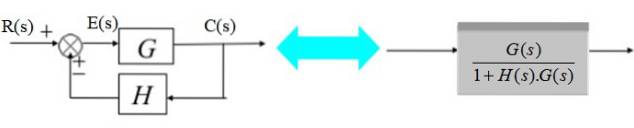
I diagrammet til høyre er utgangssignalet C (s):

C (s) = E (s). G (s) med E (s) = R (s) - C (s). H (s)

Deretter:

C (s) = [R (s) - C (s). H (s)]. G (s)

C (s) [1+ H (s) .G (s)] = R (s) .G (s)

Derfor kan C (s) løses ved:

C (s) = G (s). R (s) / [1+ H (s) .G (s)]

Og overføringsfunksjonen vil være:

G (s) / [1+ H (s) .G (s)]

Som vist i det forenklede diagrammet til høyre.

Løst øvelser

Øvelse 1

Finn overføringsfunksjonen til følgende system:

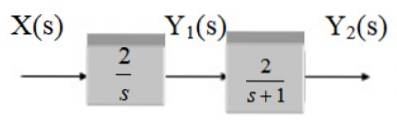
Løsning

Den behandler to blokker i kaskade, derfor er overføringsfunksjonen produktet av funksjonene G₁ og G_to.

Det må:

G₁ = 2 / s

G_to = 2 / (s + 1)

Derfor er den søkte overføringsfunksjonen:

G (s) = 4 / [s (s + 1)]

Øvelse 2

Reduser følgende system:

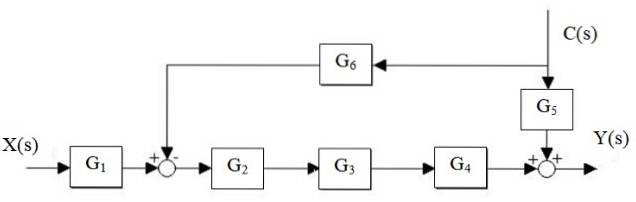
Løsning

Først reduseres G-kaskaden_to, G₃ og G_4, og parallellen G er atskilt₅ og G₆:

Deretter legger huggeren til venstre for blokk G_to ⋅G₃ ⋅ G₄ beveger seg til høyre:

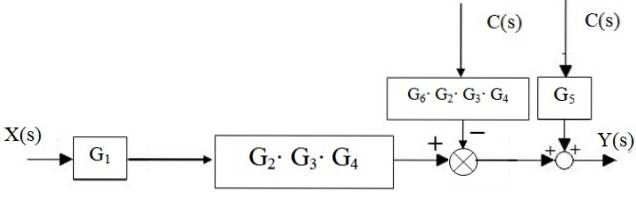
Tilleggene til høyre er redusert til bare en, i tillegg til kaskader:

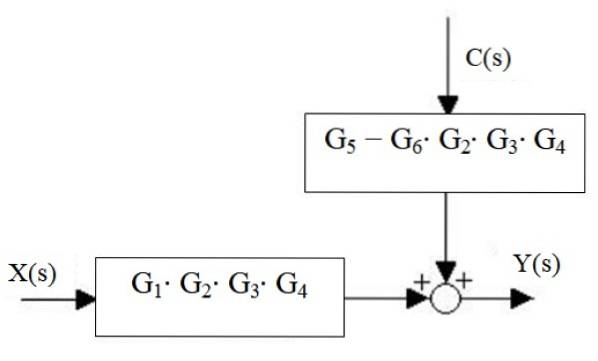
Til slutt er utdataene fra systemet:

Y (s) = X (s) ⋅G₁⋅ G_to ⋅G₃ ⋅ G₄ + C (s) ⋅ [G₅ - G₆ ⋅ G_to ⋅G₃ ⋅ G₄]

Referanser

1. Alaydi, J. Blokkdiagram for kontrollsystem. Gjenopprettet fra: site.iugaza.edu.ps.
2. Bolton, W. 2006. Kontrollteknikk. 2. plass. Utgave. Alpha Omega.
3. Cwalinsky, J. Innføring i systemblokkalgebra. Gjenopprettet fra: cedengineering.com.
4. Dademuchconnection. Blokkdiagram. Gjenopprettet fra: dademuch.com.
5. Ogata, K. 2010. Moderne kontrollteknikk. 5. Utgave. Pearson.