
Vector Algebra Fundamentals, Magnitudes, Vectors
De vektor algebra er en gren av matematikk som har ansvar for å studere systemer for lineære ligninger, vektorer, matriser, vektorrom og deres lineære transformasjoner. Det er relatert til områder som engineering, oppløsning av differensiallikninger, funksjonsanalyse, operasjonsforskning, datagrafikk, blant andre..
Et annet område som lineær algebra har tatt i bruk er fysikk, siden det gjennom dette har vært mulig å utvikle studiet av fysiske fenomener, som beskriver dem ved bruk av vektorer. Dette har muliggjort en bedre forståelse av universet.

Artikkelindeks
- 1 Grunnleggende
- 1.1 Geometrisk
- 1.2 Analytisk
- 1.3 Aksiomatisk
- 2 størrelser
- 2.1 Skala størrelse
- 2.2 Vektorstørrelse
- 3 Hva er vektorer?
- 3.1 Modul
- 3.2 Adresse
- 3.3 Følelse
- 4 Klassifisering av vektorer
- 4.1 Fast vektor
- 4.2 Gratis vektor
- 4.3 Skyvevektor
- 5 Egenskaper for vektorer
- 5.1 teamlinsevektorer
- 5.2 Tilsvarende vektorer
- 5.3 Likestilling av vektorer
- 5.4 Motsatte vektorer
- 5.5 Enhetsvektor
- 5.6 Nullvektor
- 6 Komponenter i en vektor
- 6.1 Eksempler
- 7 Operasjoner med vektorer
- 7.1 Addisjon og subtraksjon av vektorer
- 7.2 Multiplikasjon av vektorer
- 8 Referanser
Grunnleggende
Vektoralgebra stammer fra studien av kvaternioner (utvidelse av reelle tall) 1, i, j og k, samt fra den kartesiske geometrien promotert av Gibbs og Heaviside, som innså at vektorer ville tjene som et instrument for å representere ulike fysiske fenomen.
Vektoralgebra studeres gjennom tre grunnleggende:
Geometrisk
Vektorer er representert med linjer som har en orientering, og operasjoner som addisjon, subtraksjon og multiplikasjon med reelle tall defineres gjennom geometriske metoder..
Analytisk
Beskrivelsen av vektorer og deres operasjoner gjøres med tall, kalt komponenter. Denne typen beskrivelse er resultatet av en geometrisk fremstilling fordi et koordinatsystem brukes.
Aksiomatisk
En beskrivelse av vektorene er laget, uavhengig av koordinatsystemet eller hvilken som helst type geometrisk fremstilling.
Studiet av figurer i rommet gjøres gjennom deres representasjon i et referansesystem, som kan ha en eller flere dimensjoner. Blant de viktigste systemene er:
- Endimensjonalt system, som er en linje der et punkt (O) representerer opprinnelsen og et annet punkt (P) bestemmer skalaen (lengden) og dens retning:
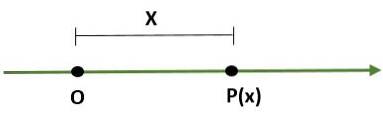
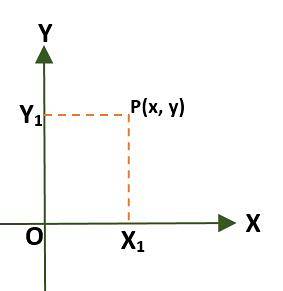
- Rektangulært koordinatsystem (todimensjonalt), som består av to vinkelrette linjer kalt x-aksen og y-aksen, som passerer gjennom et punkt (O) opprinnelse; på denne måten er flyet delt inn i fire regioner som kalles kvadranter. I dette tilfellet er et punkt (P) i planet gitt av avstandene mellom aksene og P.
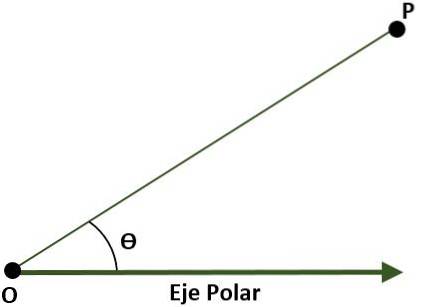
- Polarkoordinatsystem (todimensjonalt). I dette tilfellet er systemet sammensatt av et punkt O (opprinnelse) som kalles polen og en stråle med opprinnelse i O kalt polaraksen. I dette tilfellet blir punktet P på planet, med referanse til polen og polaraksen, gitt av vinkelen (Ɵ), som dannes av avstanden mellom opprinnelsen og punktet P.
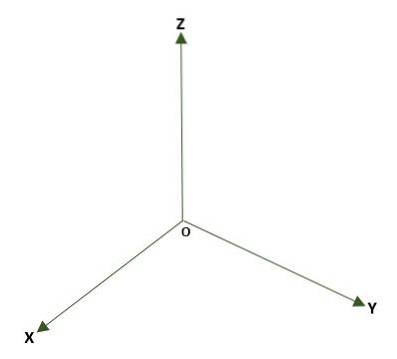
- Rektangulært tredimensjonalt system, dannet av tre vinkelrette linjer (x, y, z) hvis opprinnelse er et punkt O i rommet. Tre koordinatplaner dannes: xy, xz og yz; rommet vil bli delt inn i åtte regioner som kalles oktanter. Henvisningen til et punkt P i rommet er gitt av avstandene mellom flyene og P.
Størrelser
En størrelse er en fysisk størrelse som kan telles eller måles gjennom en numerisk verdi, som i tilfelle noen fysiske fenomener; det er imidlertid ofte nødvendig å kunne beskrive disse fenomenene med andre faktorer enn numeriske. Derfor er størrelsesorden klassifisert i to typer:
Skala størrelse
De er de størrelsene som er definert og representert numerisk; det vil si av en modul sammen med en måleenhet. For eksempel:
a) Tid: 5 sekunder.
b) Masse: 10 kg.
c) Volum: 40 ml.
d) Temperatur: 40 ºC.
Vector størrelse
De er de størrelsene som er definert og representert av en modul sammen med en enhet, så vel som en sans og retning. For eksempel:
a) Hastighet: (5ȋ - 3ĵ) m / s.
b) Akselerasjon: 13 m / sto; S 45º E.
c) Kraft: 280 N, 120 °.
d) Vekt: -40 ĵ kg-f.
Vektormengder er representert grafisk av vektorer.
Hva er vektorer?
Vektorer er grafiske representasjoner av en vektormengde; det vil si at de er linjesegmenter der den endelige enden er tuppen av en pil.
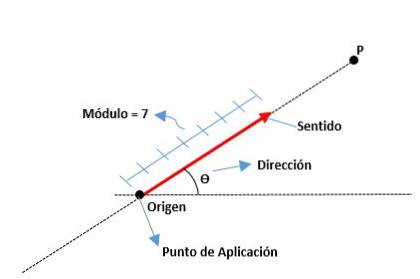
Disse bestemmes av modulens eller segmentlengden, retningen, som er indikert av pilspissen, og retningen i henhold til linjen den tilhører. Opprinnelsen til en vektor er også kjent som applikasjonspunktet.
Elementene til en vektor er som følger:
Modul
Det er avstanden fra opprinnelsen til slutten av en vektor, representert med et reelt tall sammen med en enhet. For eksempel:
| OM | = | A | = A = 6 cm
Retning
Det er målet for vinkelen som eksisterer mellom x-aksen (fra det positive) og vektoren, så vel som kardinalpunktene (nord, sør, øst og vest) brukes.
Føle
Den er gitt av pilspissen som er plassert på enden av vektoren, og indikerer hvor den skal.
Klassifisering av vektorer
Generelt er vektorer klassifisert som:
Fast vektor
Det er en hvis brukspunkt (opprinnelse) er løst; det vil si at den forblir knyttet til et punkt i rommet, så den kan ikke bevege seg i dette.
Gratis vektor
Den kan bevege seg fritt i rommet fordi opprinnelsen beveger seg til et hvilket som helst punkt uten å endre modul, retning eller retning..
Skyvevektor
Det er en som kan overføre sin opprinnelse langs sin handlingslinje uten å endre modul, retning eller retning..
Egenskaper av vektorer
Blant de viktigste egenskapene til vektorer er følgende:
Vektorer teamlinser
De er de gratis vektorene som har samme modul, retning (eller de er parallelle) og forstår som en skyvevektor eller en fast vektor.
Tilsvarende vektorer
Det oppstår når to vektorer har samme retning (eller er parallelle), samme sans, og til tross for at de har forskjellige moduler og applikasjonspunkter, forårsaker de samme effekter.
Vectorlikhet
Disse har samme modul, retning og sans, selv når utgangspunktene er forskjellige, noe som gjør at en parallell vektor kan oversette seg selv uten å påvirke den..
Motsatte vektorer
De er de som har samme modul og retning, men deres sans er motsatt.
Enhetsvektor
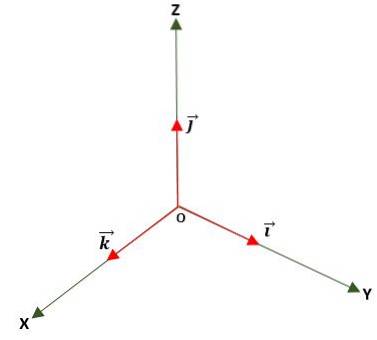
Det er en der modulen er lik enheten (1). Dette oppnås ved å dele vektoren med modulen og brukes til å bestemme retning og følelse av en vektor, enten i planet eller i rommet, ved hjelp av basen eller normaliserte enhetsvektorer, som er:
Null vektor
Det er den hvis modul er lik 0; det vil si at dens utgangspunkt og slutt sammenfaller på samme punkt.
Komponenter i en vektor
Komponentene i en vektor er de verdiene til vektorens projeksjoner på aksene til referansesystemet; Avhengig av dekomponering av vektoren, som kan være på to- eller tredimensjonale akser, vil man få henholdsvis to eller tre komponenter..
Komponentene i en vektor er reelle tall, som kan være positive, negative eller til og med null (0).
Således, hvis vi har en vektor Ā, med opprinnelse i et rektangulært koordinatsystem i xy-planet (todimensjonalt), er projeksjonen på x-aksen Āx og projeksjonen på y-aksen er Āy. Dermed vil vektoren bli uttrykt som summen av komponentvektorene.
Eksempler
Første eksempel
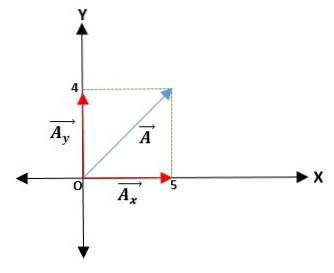
Vi har en vektor Ā som starter fra opprinnelsen og koordinatene til dens ender er gitt. Dermed er vektoren Ā = (Āx; TILY) = (4; 5) cm.
Hvis vektoren Ā virker ved opprinnelsen til et tredimensjonalt trekantet koordinatsystem (i rommet) x, y, z, til et annet punkt (P), vil projeksjonene på aksene være Āx, Āy og Āz; således vil vektoren uttrykkes som summen av dens tre komponentvektorer.
Andre eksempel
Vi har en vektor Ā som starter fra opprinnelsen og koordinatene til dens ender er gitt. Dermed er vektoren Ā = (Ax; TILY; TILz) = (4; 6; -3) cm.
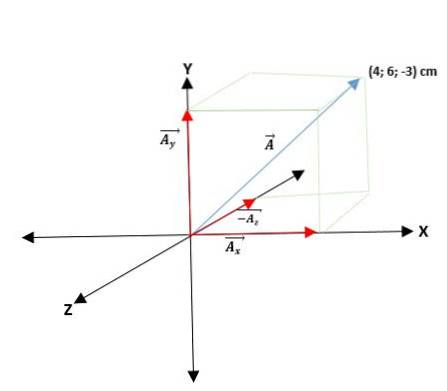
Vektorer som har sine rektangulære koordinater kan uttrykkes som basisvektorer. For det trenger du bare å multiplisere hver koordinat med sin respektive enhetsvektor, på en slik måte at de for flyet og rommet vil være følgende:
For flyet: Ā = Axi + A.Yj.
For rommet: Ā = A.xi + A.Yj + A.zk.
Vector operasjoner
Det er mange størrelser som har en modul, sans og retning, som akselerasjon, hastighet, forskyvning, kraft, blant andre..
Disse brukes i forskjellige vitenskapsområder, og for å anvende dem er det i noen tilfeller nødvendig å utføre operasjoner som addisjon, subtraksjon, multiplikasjon og deling av vektorer og skalarer..
addisjon og subtraksjon av vektorer
Tilsetting og subtraksjon av vektorer regnes som en enkelt algebraisk operasjon fordi subtraksjonen kan skrives som en sum; for eksempel kan subtraksjonen av vektorene Ā og Ē uttrykkes som:
Ā - Ē = Ā + (-Ē)
Det er forskjellige metoder for å utføre addisjon og subtraksjon av vektorer: de kan være grafiske eller analytiske.
Grafiske metoder
Brukes når en vektor har en modul, sans og retning. For dette tegnes linjer som danner en figur som senere hjelper til med å bestemme resultatet. Blant de mest kjente er følgende:
Parallelogrammetode
For å gjøre addisjonen eller subtraksjonen av to vektorer, velges et felles punkt på koordinataksen - som vil representere vektorenes opprinnelsespunkt - og holde modul, retning og retning..
Linjer tegnes deretter parallelt med vektorene for å danne et parallellogram. Den resulterende vektoren er diagonalen som går fra opprinnelsespunktet til begge vektorene til toppunktet til parallellogrammet:
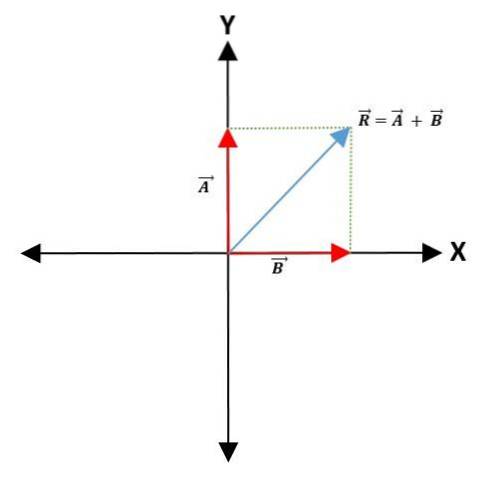
Trekantmetode
I denne metoden er vektorene plassert etter hverandre, med moduler, retninger og retninger. Den resulterende vektoren vil være foreningen av opprinnelsen til den første vektoren med slutten av den andre vektoren:
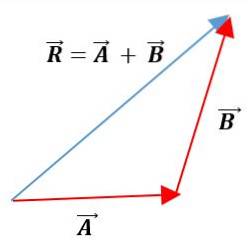
Analytiske metoder
To eller flere vektorer kan legges til eller trekkes fra ved hjelp av en geometrisk eller vektormetode:
Geometrisk metode
Når to vektorer danner et trekant eller parallellogram, kan modulen og retningen til den resulterende vektoren bestemmes ved hjelp av lovene til sinus og cosinus. Dermed er modulen til den resulterende vektoren, som anvender cosinusloven og ved trekantmetoden, gitt av:
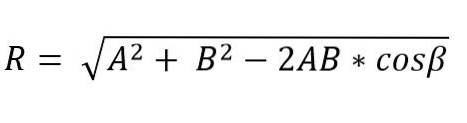
I denne formelen er β vinkelen motsatt siden R, og denne er lik 180º - Ɵ.
I stedet for, ved hjelp av parallellogrammetoden, er modulen til den resulterende vektoren:
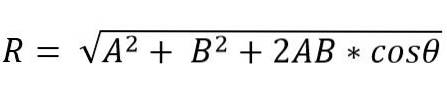
Retningen til den resulterende vektoren er gitt av vinkelen (α), som danner den resulterende med en av vektorene.
Ved sinusloven kan tillegg eller subtraksjon av vektorer også gjøres ved hjelp av trekanten eller parallellogrammetoden, vel vitende om at sidene i hver trekant er proporsjonale med vinklene:
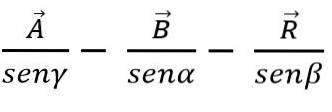
Vektormetode
Dette kan gjøres på to måter: avhengig av dets rektangulære koordinater eller basisvektorene.
Det kan gjøres ved å oversette vektorene som skal legges til eller trekkes ut mot koordinatens opprinnelse, og deretter alle projeksjonene på hver av aksene for planet (x, y) eller mellomrom (x og Z); til slutt blir komponentene lagt til algebraisk. Så for flyet er det:
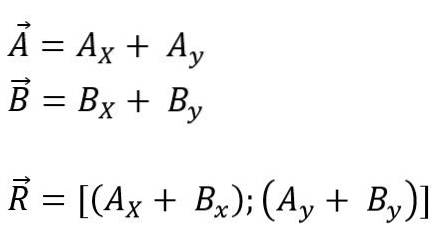
Modulen til den resulterende vektoren er:
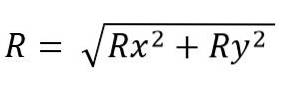
Mens det er plass:
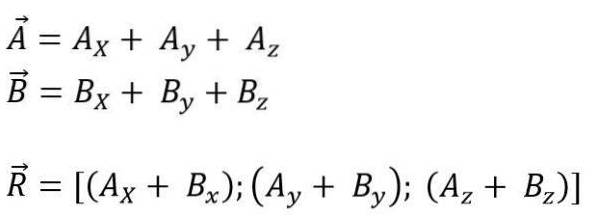
Modulen til den resulterende vektoren er:
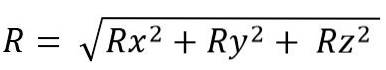
Når vektorsummer utføres, brukes flere egenskaper, som er:
- Assosiativ egenskap: den resulterende endres ikke når du legger til to vektorer først, og deretter legger til en tredje vektor.
- Kommutativ eiendom: rekkefølgen på vektorene endrer ikke resultatet.
- Vektordistribusjonsegenskap: Hvis en skalar multipliseres med summen av to vektorer, er den lik multiplikasjonen av skalaren med hver vektor.
- Skalærfordelingsegenskap: Hvis en vektor multipliseres med summen av to skalarer, er den lik multiplikasjonen av vektoren for hver skalar.
Multiplikasjon av vektorer
Multiplikasjonen eller produktet av vektorer kan gjøres som addisjon eller subtraksjon, men å gjøre det på den måten mister den fysiske betydningen og blir nesten aldri funnet i applikasjoner. Derfor er vanligvis de mest brukte produkttypene skalar- og vektorproduktet.
Scalar produkt
Det er også kjent som prikkproduktet til to vektorer. Når modulene til to vektorer multipliseres med cosinus med den minste vinkelen dannet mellom dem, oppnås en skalar. For å uttrykke et skalarprodukt mellom to vektorer, plasseres et punkt mellom dem, og dette kan defineres som:
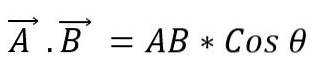
Verdien av vinkelen som eksisterer mellom de to vektorene vil avhenge av om de er parallelle eller vinkelrette; dermed må du:
- Hvis vektorene er parallelle og har samme sans, er cosinus 0º = 1.
- Hvis vektorene er parallelle og har motsatt retning, er cosinus 180º = -1.
- Hvis vektorene er vinkelrette, er cosinus 90º = 0.
Den vinkelen kan også beregnes og vite at:

Punktproduktet har følgende egenskaper:
- Kommutativ eiendom: rekkefølgen på vektorene endrer ikke skalaren.
-Fordelingsegenskap: Hvis en skalar multipliseres med summen av to vektorer, er den lik multiplikasjonen av skalaren med hver vektor.
Vector produkt
Vektormultiplikasjon, eller kryssprodukt av to vektorer A og B, vil resultere i en ny vektor C og uttrykkes ved hjelp av et kryss mellom vektorene:
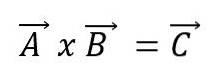
Den nye vektoren vil ha sine egne egenskaper. Den veien:
- Retningen: denne nye vektoren vil være vinkelrett på planet, som bestemmes av de opprinnelige vektorene.
- Retningen: dette bestemmes med høyre håndregel, der vektor A roteres mot B, som indikerer rotasjonsretningen med fingrene, og retningen til vektoren er markert med tommelen.
- Modulen: bestemmes av multiplikasjonen av modulene til vektorene AxB, av sinusen til den minste vinkelen som eksisterer mellom disse vektorene. Det uttrykkes:
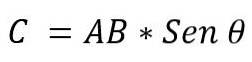
Verdien av vinkelen som eksisterer mellom de to vektorene vil avhenge av om de er parallelle eller vinkelrette. Så det er mulig å si følgende:
- Hvis vektorene er parallelle og har samme sans, er sinus 0º = 0.
- Hvis vektorene er parallelle og har motsatt retning, er sinus 180º = 0.
- Hvis vektorene er vinkelrette, er sinus 90º = 1.
Når et vektorprodukt uttrykkes som en funksjon av basisvektorene, har vi:
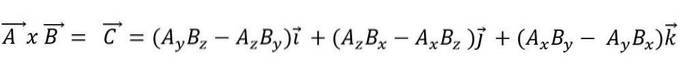
Punktproduktet har følgende egenskaper:
- Det er ikke kommutativt: rekkefølgen på vektorene endrer skalaren.
- Fordelingsegenskap: Hvis en skalar multipliseres med summen av to vektorer, er den lik multiplikasjonen av skalaren med hver vektor.
Referanser
- Altman Naomi, M. K. (2015). "Enkel lineær regresjon." Naturmetoder .
- Angel, A. R. (2007). Elementær algebra. Pearson Education,.
- Arthur Goodman, L. H. (1996). Algebra og trigonometri med analytisk geometri. Pearson Education.
- Gusiatnikov, P., og Reznichenko, S. (s.f.). Vektoralgebra i eksempler. Moskva: Mir.
- Lay, D.C. (2007). Lineær algebra og dens applikasjoner. Pearson Education.
- Llinares, J. F. (2009). Lineær algebra: Vektorrom. Euklidisk vektorplass. Universitetet i Alicante.
- Mora, J. F. (2014). Lineær algebra. Hjemland.



Ingen har kommentert denne artikkelen ennå.