
Vinkelrette linjekarakteristikker, eksempler, øvelser
EN vinkelrett linje Det er en som danner en vinkel på 90 ° i forhold til en annen linje, kurve eller overflate. Vær oppmerksom på at når to linjer er vinkelrette og er på samme plan, danner de fire identiske vinkler, hver på 90º når de krysser hverandre..
Hvis en av vinklene ikke er 90 °, sies det at linjene er skrå. Vinkelrette linjer er vanlige i design, arkitektur og konstruksjon, for eksempel nettverket av rør i følgende bilde.

Retningen til de vinkelrette linjene kan være forskjellig, slik som de som er vist nedenfor:
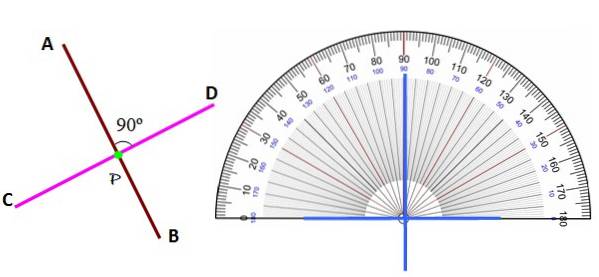
Uansett posisjon gjenkjennes linjene vinkelrett på hverandre ved å identifisere vinkelen mellom dem som 90º, ved hjelp av vinkelmåler.
Merk at i motsetning til parallelle linjer i planet, som aldri krysser hverandre, gjør vinkelrette linjer det alltid på et punkt P, kalt fot av en av linjene over den andre. Derfor er det også to vinkelrette linjer flekker.
Enhver linje har uendelige vinkelrett på den, siden bare ved å flytte segment AB til venstre eller høyre over segment CD, vil vi ha nye vinkelrett med en annen fot.
Imidlertid kalles den vinkelrette som passerer rett gjennom midtpunktet til et segment halvsnitt av nevnte segment.
Artikkelindeks
- 1 Eksempler på vinkelrette linjer
- 1.1 Flere eksempler på vinkelrette linjer
- 2 Øvelser
- 2.1 - Øvelse 1
- 2.2 - Øvelse 2
- 3 Referanser
Eksempler på vinkelrette linjer
Vinkelrette linjer er vanlige i bylandskapet. I det følgende bildet (figur 3) er bare noen få av de mange vinkelrette linjene som kan sees i den enkle fasaden til denne bygningen og dens elementer som dører, kanaler, trinn og mer blitt fremhevet:

Det gode er at tre linjer vinkelrett på hverandre hjelper oss med å etablere plasseringen av punkter og objekter i rommet. De er koordinataksene identifisert som X-akse, Akse y Y z-aksen, godt synlig i hjørnet av et rektangulært rom som det nedenfor:
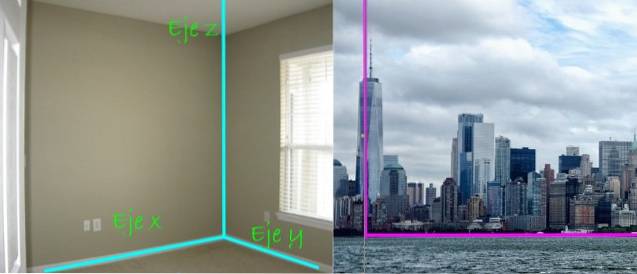
I panoramautsikten over byen, til høyre, er også vinkelrett mellom skyskraper og bakken merkbar. Den første, vil vi si, finnes langs z-aksen, mens bakken er et fly, som i dette tilfellet er flyet xy.
Hvis bakken utgjør flyet xy, skyskraperen er også vinkelrett på enhver gate eller gate, noe som garanterer stabiliteten, siden en skrånende struktur er ustabil.
Og i gatene, uansett hvor det er rektangulære hjørner, er det vinkelrette linjer. Mange veier og gater har en vinkelrett utforming, så lenge terrenget og geografiske trekk tillater det..
For å kort uttrykke vinkelrettheten mellom linjer, segmenter eller vektorer, brukes symbolet ⊥. For eksempel hvis linjen L1 er vinkelrett på linjen Lto, vi skrev:
L1 ⊥ Lto
Flere eksempler på vinkelrette linjer
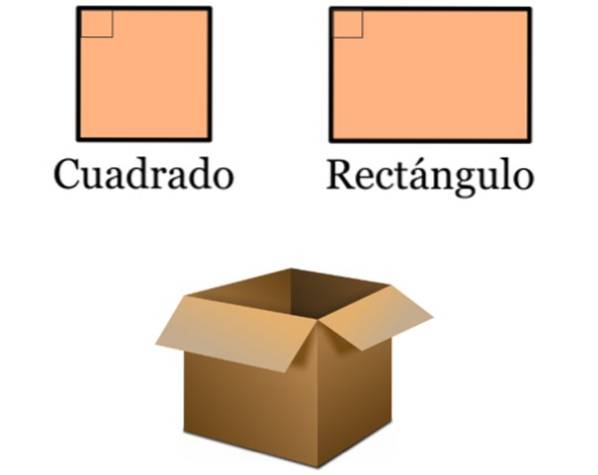
- I utformingen er de vinkelrette linjene veldig til stede, siden mange vanlige gjenstander er basert på firkanter og rektangler. Disse firkantene er preget av å ha indre vinkler på 90 º, fordi sidene er parallelle to og to:
- Feltene der forskjellige idretter praktiseres er avgrenset av mange firkanter og rektangler. Disse inneholder igjen vinkelrette linjer.
- To av segmentene som utgjør en rett trekant er vinkelrett på hverandre. Disse kalles ben, mens den resterende linjen kalles hypotenuse.
- Linjene til den elektriske feltvektoren er vinkelrett på overflaten til en leder i elektrostatisk likevekt.
- For en ladet leder er de ekvipotensielle linjene og overflatene alltid vinkelrette på det elektriske feltets.
- I rør- eller ledningssystemer som brukes til å transportere forskjellige typer væsker, for eksempel gass vist i figur 1, er vinkelrette albuer vanlige. Derfor danner de vinkelrette linjer, slik er det med et fyrrom:

Opplæring
- Øvelse 1
Tegn to vinkelrette linjer ved hjelp av linjal og kompass.
Løsning
Det er veldig enkelt å gjøre, ved å følge disse trinnene:
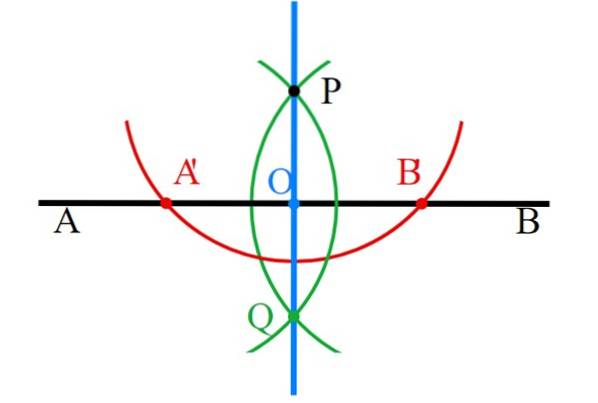
-Den første linjen er tegnet, kalt AB (svart).
-Over (eller under hvis du foretrekker det) markerer du punkt P, som vinkelrett vil passere gjennom. Hvis P er like over (eller under) midten av AB, er den vinkelrette halveringen av segmentet AB.
-Med kompasset sentrert på P, tegner du en sirkel som skjærer AB på to punkter, kalt A 'og B' (rød).
-Kompasset åpnes ved A'P, det er sentrert på A 'og en sirkel tegnes som går gjennom P (grønn).
-Gjenta forrige trinn, men nå åpner du målene lengden på segmentet B'P (grønn). Begge omkretsbuer krysses ved punkt Q under P og selvfølgelig ved sistnevnte.
-Punktene P og Q er sammenføyd med linjalen og den vinkelrette linjen (blå) er klar.
-Til slutt må alle hjelpekonstruksjonene slettes nøye, slik at bare de vinkelrette er igjen..
- Øvelse 2
To linjer L1 og jegto er vinkelrette hvis deres respektive skråninger m1 og Mto møte dette forholdet:
m1 = -1 / mto
Gitt linjen y = 5x - 2, finn en linje vinkelrett på den og som passerer gjennom punktet (-1, 3).
Løsning
-Finn først skråningen til den vinkelrette linjen m⊥, som angitt i uttalelsen. Skråningen til den opprinnelige linjen er m = 5, koeffisienten som følger med "x". Deretter:
m⊥= -1/5
-Deretter blir ligningen av den vinkelrette linjen konstruert og⊥, erstatter den tidligere funnet verdien:
Y⊥= -1 / 5x + b
-Deretter bestemmes verdien av b, ved hjelp av punktet gitt av utsagnet, (-1,3), siden den vinkelrette linjen må passere gjennom den:
y = 3
x = -1
Erstatter:
3 = -1/5 (-1) + b
Løs verdien for b:
b = 3- (1/5) = 14/5
-Endelig er den endelige ligningen bygget:
Y⊥= -1 / 5x + 14/5
Referanser
- Baldor, A. 2004. Plan- og romgeometri. Kulturelle publikasjoner.
- Clemens, S. 2001. Geometri med applikasjoner og problemløsning. Addison Wesley.
- Matematikk er gøy. Vinkelrette linjer. Gjenopprettet fra: mathisfun.com.
- Monterey Institute. Vinkelrette linjer. Gjenopprettet fra: montereyinstitute.org.
- Wikipedia. Vinkelrette linjer. Gjenopprettet fra: es.wikipedia.org.



Ingen har kommentert denne artikkelen ennå.