Invers matriseberegning og løst øvelse

De Invers matrise av en gitt matrise, er det matrisen som multipliseres med de opprinnelige resultatene i identitetsmatrisen. Den omvendte matrisen er nyttig for å løse systemer av lineære ligninger, derav viktigheten av å vite hvordan man skal beregne den.

Matriser er veldig nyttige i fysikk, ingeniørfag og matematikk, siden de er et kompakt verktøy for å løse komplekse problemer. Nytten av matriser forbedres når de er inverterbare og deres inverse er også kjent.

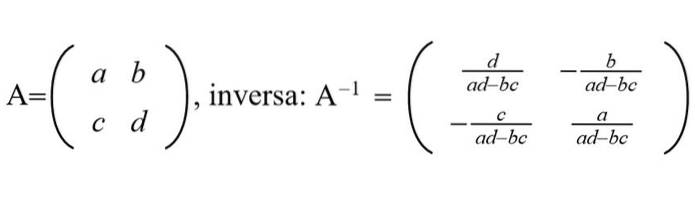
Innen grafisk prosessering, Big Data, Data Mining, Machine Learning og andre, brukes effektive og raske algoritmer for å evaluere den inverse matrisen til nxn-matriser med veldig stor n, i størrelsesorden tusenvis eller millioner.

For å illustrere bruken av den inverse matrisen til å håndtere et system med lineære ligninger, begynner vi med det enkleste tilfellet av alle: 1 × 1 matriser.

Det enkleste tilfellet: en lineær ligning av en enkelt variabel blir vurdert: 2 x = 10.

Tanken er å finne verdien av x, men det vil bli gjort "matrisemessig". 

Matrisen M = (2) som multipliserer vektoren (x) er en 1 × 1 matrise som resulterer i vektoren (10):

M (x) = (10)

Det omvendte av matrisen M er betegnet med M^-1.

Den generelle måten å skrive dette "lineære systemet" på er:

M X = B, hvor X er vektoren (x) og B er vektoren (10).

Per definisjon er den inverse matrisen en som multiplisert med den opprinnelige matrisen resulterer i identitetsmatrisen I:

M^-1 M = jeg

I tilfellet vurderes matrisen M^-1 er matrisen (½), det vil si M^-1 = (½) siden M^-1 M = (½) (2) = (1) = I

For å finne den ukjente vektoren X = (x), i den foreslåtte ligningen, multipliseres begge medlemmer med den inverse matrisen:

M^-1 M (x) = M^-1 (10)

(½) (2) (x) = (½) (10)

(½ 2) (x) = (½ 10)

(1) (x) = (5)

(x) = (5)

En likhet med to vektorer er nådd, som bare er like når de tilsvarende elementene er like, det vil si x = 5.

Beregning av det inverse av en matrise

Det som motiverer beregningen av den inverse matrisen, er å finne en universell metode for løsning av lineære systemer som følgende 2 × 2-system:

x - 2 y = 3

-x + y = -2

Etter trinnene i 1 × 1-saken, studert i forrige avsnitt, skriver vi ligningssystemet i matriseform:

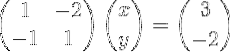
Merk at dette systemet er skrevet i kompakt vektornotasjon som følger:

M X = B

hvor

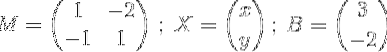
Det neste trinnet er å finne det omvendte av M.

Metode 1: Bruke Gaussisk eliminering

Den Gaussiske eliminasjonsmetoden vil bli brukt. Som består i å gjøre elementære operasjoner på radene til matrisen, disse operasjonene er:

- Multipliser en rad med et tall som ikke er null.

- Legg til eller trekk fra en rad en annen rad, eller flere av en annen rad.

- Bytt rad.

Målet er å konvertere den opprinnelige matrisen til identitetsmatrisen gjennom disse operasjonene. 

Når dette er gjort, brukes nøyaktig de samme operasjonene i matrise M til identitetsmatrisen. Når etter flere operasjoner på radene M blir transformert til enhetsmatrisen, vil den som opprinnelig var enheten bli transformert til den inverse matrisen til M, det vil si M^-1.

1- Vi begynner prosessen med å skrive matrisen M og ved siden av enheten matrisen:

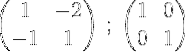
2- Vi legger til de to radene, og vi legger resultatet i den andre raden, på denne måten får vi null i det første elementet i den andre raden:

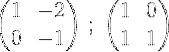
3- Vi ganger den andre raden med -1 for å oppnå 0 og 1 på den andre raden:

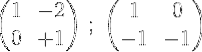
4- Den første raden multipliseres med ½:

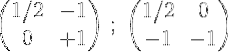
5- Det andre og det første legges til og resultatet plasseres i første rad:

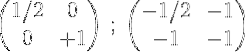
6- For å fullføre prosessen, multipliser den første raden med 2 for å oppnå identitetsmatrisen i den første raden og den inverse matrisen til den opprinnelige matrisen M i den andre:

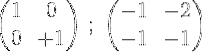
Nemlig:

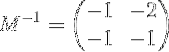
Systemløsning

Når den inverse matrisen er oppnådd, fortsetter vi med å løse ligningssystemet ved å bruke den inverse matrisen på begge delene av den kompakte vektorligningen:

M^-1M X = M^-1B

X = M^-1B

Som eksplisitt ser slik ut:

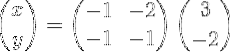
Deretter utføres matriksmultiplikasjon for å oppnå vektor X:

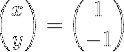
Metode 2: Bruk vedlagt matrise

I denne andre metoden beregnes den inverse matrisen med utgangspunkt i den tilstøtende matrisen til den opprinnelige matrisen TIL.

Anta en matrise A gitt av:

hvor til_{jeg, j} er elementet i raden Jeg og kolonnen j av matrisen TIL.

Tilgrensningen til matrisen TIL det vil bli kalt Adj (A) og dets elementer er:

annonse_{jeg, j} = (-1)^{(i + j)} ¦Ai, j¦

hvor Ai, j er den komplementære mindre matrisen oppnådd ved å eliminere rad i og kolonne j fra den opprinnelige matrisen TIL. Stolpene ¦ ¦ indikerer at determinanten beregnes, altså ¦Ai, j¦ er determinanten for den komplementære mindre matrisen.

Invers matriseformel

Formelen for å finne den omvendte matrisen som starter fra den tilstøtende matrisen til den opprinnelige matrisen er følgende:

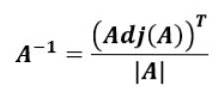
Det vil si den omvendte matrisen til TIL, TIL^-1, er transponere av tilknytningen til TIL delt på determinanten av TIL.

Transponere TIL^Tav en matrise TIL er den som oppnås ved å bytte rader mot kolonner, det vil si at den første raden blir den første kolonnen og den andre raden blir den andre kolonnen og så videre til n radene i den opprinnelige matrisen er fullført.

Treningen løst

La matrisen A være følgende:

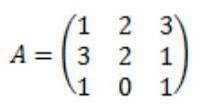
Hvert eneste element i den tilgrensende matrisen til A beregnes: Adj (A)

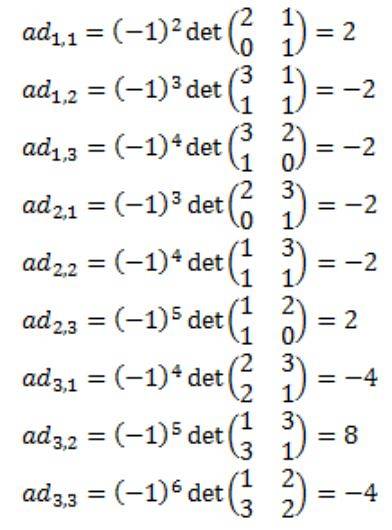
Det resulterer i at den tilgrensende matrisen til A, Adj (A) er følgende:

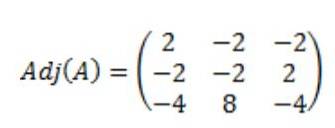
Deretter beregnes determinanten for matrise A, det (A):

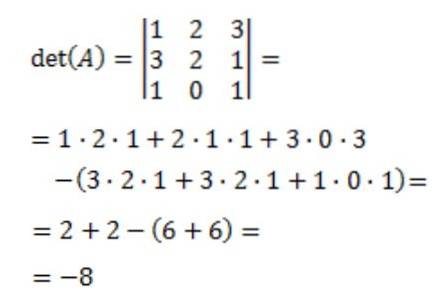
Til slutt oppnås den omvendte matrisen til A:

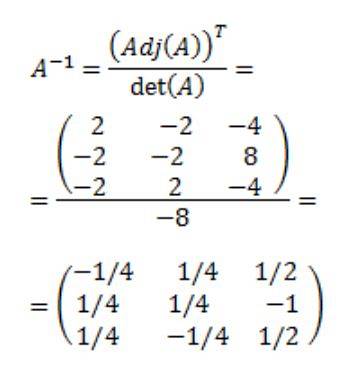
Referanser

1. Anthony Nicolaides (1994) Determinants & Matrices. Bestå publikasjon.
2. Awol Assen (2013) En studie om beregning av determinanter av en 3 × 3
3. Casteleiro Villalba M. (2004) Introduksjon til lineær algebra. ESIC-redaksjon.
4. Dave Kirkby (2004) Maths Connect. Heinemann.
5. Jenny Olive (1998) Maths: A Students Survival Guide. Cambridge University Press.
6. Richard J. Brown (2012) 30-Second Maths: The 50 Most Mind-Expanding Theories in Mathematics. Ivy press begrenset.
7. Matrise. Lap Lambert Academic Publishing.