Målinger av posisjon, sentral tendens og spredning

De mål på sentral tendens, spredning og posisjon, er verdier som brukes til å tolke et sett med statistiske data riktig. Disse kan bearbeides direkte, ettersom de er hentet fra den statistiske studien, eller de kan organiseres i grupper med like frekvens, noe som letter analysen..

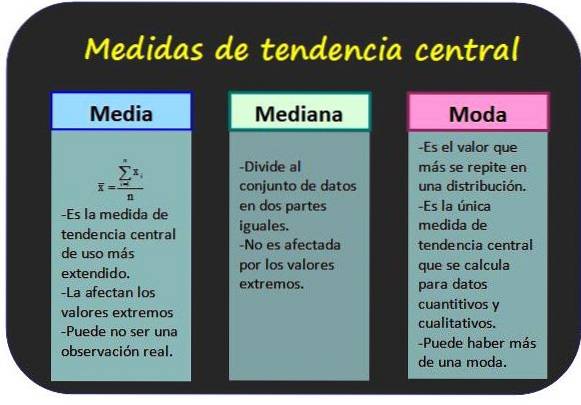
Tiltak for sentral tendens

De tillater å vite rundt hvilke verdier de statistiske dataene er gruppert.

Aritmetisk gjennomsnitt

Det er også kjent som gjennomsnittet av verdiene til en variabel og oppnås ved å legge til alle verdiene og dele resultatet med det totale antall data.

• Aritmetisk gjennomsnitt for ikke-grupperte data

La være en variabel x som vi har n data uten å organisere eller gruppere, beregnes dens aritmetiske gjennomsnitt som følger:

Og i summeringsnotasjon:

Eksempel

Eierne av et fjellturisthus har til hensikt å vite hvor mange dager i gjennomsnitt besøkende blir i fasilitetene. For dette ble det ført en oversikt over varighetene til 20 grupper turister, og innhentet følgende data:

1; 1; to; to; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; to; to; 3; 4; 1

Gjennomsnittlig antall dager turister oppholder seg er:

• Aritmetisk gjennomsnitt for grupperte data

Hvis dataene til variabelen er organisert i en tabell over absolutte frekvenser f_Jeg og klassesentrene er x₁, x_to,..., x_n, gjennomsnittet beregnes av:

I summeringsnotasjon:

Median

Medianen for en gruppe n-verdier for variabelen x er den sentrale verdien av gruppen, forutsatt at verdiene er ordnet i økende rekkefølge. På denne måten er halvparten av alle verdier mindre enn modusen, og den andre halvparten er større..

• Median av ikke-grupperte data

Følgende tilfeller kan forekomme:

-Antall n av verdiene til variabelen x  merkelig: medianen er verdien som er midt i gruppen av verdier:

-Antall n av verdiene til variabelen x par: i dette tilfellet beregnes medianen som gjennomsnittet av de to sentrale verdiene i datagruppen:

Eksempel

For å finne medianen for dataene fra turistherberget bestilles de først fra laveste til høyeste:

1; 1; 1; 1; 1; 1; 1; to; to; to; to; 3; 3; 3; 4; 4; 4; 4; 5; 5

Antall data er jevnt, derfor er det to sentrale data: X₁₀ og X_elleve og siden begge er verdt 2, er gjennomsnittet også.

Median = 2

• Median av samlede data

Følgende formel brukes:

Symbolene i formelen betyr:

-c: bredden på intervallet som inneholder medianen

-B_M: nedre grense for samme intervall

-F_m: antall observasjoner i intervallet som medianen tilhører.

-n: totale data.

-F_BM: antall observasjoner før av intervallet som inneholder medianen.

mote

Modusen for ikke-grupperte data er verdien med høyest frekvens, mens for grupperte data er den klassen med høyest frekvens. Mote regnes som de mest representative dataene eller klassen for distribusjonen.

To viktige kjennetegn ved dette tiltaket er at et datasett kan ha mer enn en modus, og modusen kan bestemmes for både kvantitative og kvalitative data..

Eksempel

Fortsetter med dataene fra turistparadoren, er den som gjentas mest, 1, derfor er det vanligste at turister blir 1 dag i paradoren.

Tiltak for spredning

Målinger av spredning beskriver hvor gruppert dataene er rundt de sentrale målene.

Rang

Det beregnes ved å trekke de største og minste dataene. Hvis denne forskjellen er stor, er det et tegn på at dataene er spredt, mens små verdier indikerer at dataene er nær gjennomsnittet..

Eksempel

Rekkevidden for dataene til turistparadoren er:

Rekkevidde = 5−1 = 4

Forskjell

• Avvik for ikke-grupperte data

For å finne variansen s^to Det kreves å først kjenne det aritmetiske gjennomsnittet, deretter beregnes den kvadratiske forskjellen mellom hvert stykke data og gjennomsnittet, alle blir lagt til og delt på totalt antall observasjoner. Disse forskjellene er kjent som avvik.

Variansen, som alltid er positiv (eller null), indikerer hvor langt observasjonene er fra gjennomsnittet: hvis avviket er høyt, er verdiene mer spredt enn når variansen er liten.

Eksempel

Avviket for dataene fra turistherberget er:

1; 1; to; to; 1; 4; 5; 1; 3; 4; 5; 4; 3; 1; 1; to; to; 3; 4; 1

• Avvik for grupperte data

For å finne variansen til et gruppert datasett, kreves følgende: i) gjennomsnittet, ii) frekvensen f_Jeg  som er de totale dataene i hver klasse og iii) x_Jeg  eller klasseverdi:

Standardavviket er den positive kvadratroten til variansen, så den har en fordel i forhold til variansen: den kommer i de samme enhetene som variabelen som studeres, og dermed har du en mer direkte ide om hvor nær eller langt variabelen er fra gjennomsnittet.

• Standardavvik for ikke-grupperte data

Det bestemmes ganske enkelt ved å finne kvadratroten til variansen for ikke-grupperte data:

Standardavviket for dataene fra turistherberget er:

s = √ (s^to) = √1.95 = 1.40

• Standardavvik for grupperte data

Det beregnes ved å finne kvadratroten til variansen for grupperte data:

Posisjonsmålinger

Måling av posisjon deler et ordnet datasett i like store deler. Medianen, i tillegg til å være et mål på sentral tendens, er også et mål på posisjon, siden den deler helheten i to like store deler. Men mindre deler kan fås med kvartiler, desiler og persentiler.

Kvartiler

Kvartilene deler settet i fire like deler, som hver inneholder 25% av dataene. De er betegnet som Q₁, Spørsmål_to og Q₃ og medianen er kvartilen Q_to. På denne måten er 25% av dataene under Q-kvartilen.₁, 50% under Q-kvartilen_to eller median og 75% under Q-kvartilen₃.

• Kvartiler for ikke-grupperte data

Dataene er bestilt, og totalen er delt inn i 4 grupper med samme antall data hver. Posisjonen til den første kvartilen er funnet av:

Spørsmål₁ = (n + 1) / 4

Hvor n er de totale dataene. Hvis resultatet er et helt tall, blir dataene som tilsvarer den posisjonen lokalisert, men hvis det er desimal, blir dataene som tilsvarer heltallets gjennomsnitt beregnet med det neste, eller for større presisjon interpoleres det lineært mellom nevnte data.

Eksempel

Posisjonen til den første kvartilen Q₁ for dataene til turistparadoren er:

Spørsmål₁ = (n + 1) / 4 = (20 + 1) / 4 = 5,25

Dette er posisjonen til kvartil 1, og siden resultatet er desimal, blir dataene X søkt₅ og X_6, som er henholdsvis X₅ = 1 og X₆ = 1 og er gjennomsnitt, noe som resulterer i:

Første kvartil = 1

1; 1; 1; 1; 1; 1; 1; to; to; to; to; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Posisjonen til andre kvartil Q_to Det er:

Spørsmål_to = 2 (n + 1) / 4 = 10,5

Hva er gjennomsnittet mellom X₁₀ og X_elleve og samsvarer medianen:

Andre kvartil = Median = 2

Posisjonen til den tredje kvartilen beregnes av:

Spørsmål₃ = 3 (n + 1) / 4 = 3 (20 + 1) / 4 = 15,75

Det er også desimal, derfor blir X gjennomsnittet_femten og X₁₆:

1; 1; 1; 1; 1; 1; 1; to; to; to; to; 3; 3; 3; 4; 4; 4; 4; 5; 5.

Men siden begge er verdt 4:

Tredje kvartil = 4

Den generelle formelen for plassering av kvartiler i ugrupperte data er:

Spørsmål_k = k (n + 1) / 4

Med k = 1,2,3.

• Kvartiler for grupperte data

De beregnes på samme måte som medianen:

Forklaringen på symbolene er:

-B_Spørsmål: nedre grense for intervallet som inneholder kvartilen

-c: bredden på det intervallet

-F_hva: antall observasjoner i kvartilintervallet.

-n: totale data.

-F_BQ: antall data før av intervallet som inneholder kvartilen.

Deciler og persentiler

Desiler og persentiler deler datasettet i henholdsvis 10 like deler og 100 like deler, og beregningen deres utføres på en lignende måte som kvartilene.

• Deciler og persentiler for ikke-grupperte data

Formlene brukes henholdsvis:

D_k = k (n + 1) / 10

Med k = 1,2,3… 9.

Decile D₅ må være lik medianen.

P_k = k (n + 1) / 100

Med k = 1,2,3… 99.

P-persentilen_femti må være lik medianen.

Eksempel

I eksemplet med turistherberget, posisjonen til D₃ Det er:

D₃ = 3 (20 + 1) / 10 = 6,3

Siden det er et desimaltall, blir X gjennomsnittet₆ og X_7, begge er like 1:

1; 1; 1; 1; 1; 1; 1; to; to; to; to; 3; 3; 3; 4; 4; 4; 4; 5; 5

Det betyr at 3 tideler av dataene er under X₇ = 1 og de resterende over.

• Deciler og persentiler for grupperte data

Formlene er analoge med de for kvartiler. D brukes til å betegne desiler og P for persentiler, og symbolene tolkes på samme måte:

Den empiriske regelen

Når dataene er symmetrisk fordelt og fordelingen er unimodal, er det en regel som kalles  empirisk regel eller regel 68 - 95 - 99, som grupperer dem i følgende intervaller:

• 68% av dataene er i området:

• 95% av dataene er i området:

• 99% av dataene er i området:

Eksempel

I hvilket intervall er 95% av dataene fra turistparadoren?

De er i intervallet: [2.5−1.40; 2,5 + 1,40] = [1,1; 3.9].

Referanser

1. Berenson, M. 1985. Statistikk for ledelse og økonomi. Interamericana S.A.
2. Devore, J. 2012. Sannsynlighet og statistikk for ingeniørvitenskap og vitenskap. 8. plass. Utgave. Cengage.
3. Levin, R. 1988. Statistikk for administratorer. 2. plass. Utgave. Prentice hall.
4. Spiegel, M. 2009. Statistikk. Schaum-serien. 4. plass Utgave. Mcgraw hill.
5. Walpole, R. 2007. Sannsynlighet og statistikk for ingeniørfag og vitenskap. Pearson.