
Euler-metoden hva den er til, prosedyre og øvelser
De Eulers metode er den mest grunnleggende og enkle av prosedyrene som brukes for å finne tilnærmet numeriske løsninger på en vanlig differensialligning av første orden, forutsatt at den opprinnelige tilstanden er kjent.
En vanlig differensialligning (ODE) er ligningen som relaterer en ukjent funksjon av en enkelt uavhengig variabel med dens derivater.
Hvis det største derivatet som vises i ligningen er av grad 1, er det en vanlig differensialligning av første grad.
Den mest generelle måten å skrive en ligning av første grad er:

x = x0
y = y0
Artikkelindeks
- 1 Hva er Eulers metode?
- 2 Løst øvelser
- 2.1 Øvelse 1
- 2.2 Øvelse 2
- 2.3 Øvelse 3
- 3 Newtons dynamikk og Eulers metode
- 3.1 Øvelse 4
- 4 Øvelser foreslått for hjemmet
- 4.1 Øvelse 1
- 4.2 Øvelse 2
- 5 Referanser
Hva er Eulers metode?
Ideen med Eulers metode er å finne en numerisk løsning på differensiallikningen i intervallet mellom X0 og XF .
Først diskuteres intervallet i n + 1 poeng:
x0, x1, xto, x3..., xn
Som oppnås slik:
xJeg= x0+ih
Hvor h er bredden eller trinnet til delintervallene:

Med den opprinnelige tilstanden er det også mulig å kjenne derivatet i begynnelsen:
y '(xeller) = f (xeller, Yeller)
Dette derivatet representerer hellingen til tangentlinjen til kurven til funksjonen y (x) nøyaktig ved punktet:
Ao = (xeller, Yeller)
Deretter foretas en omtrentlig prediksjon av verdien til funksjonen y (x) på følgende punkt:
y (x1) ≈ og1
Y1 = Yeller +(x1- xeller) f (xeller, Yeller) = ogeller + h f (xeller, Yeller)
Det neste omtrentlige punktet i løsningen er da oppnådd, som vil svare til:
TIL1 = (x1, Y1)
Prosedyren gjentas for å oppnå de påfølgende poengene
TILto, TIL3..., xn
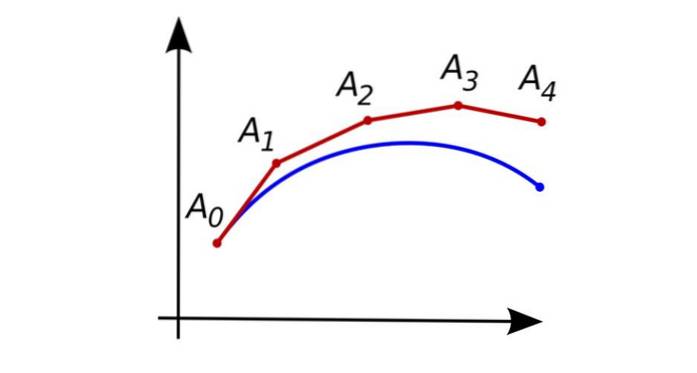
I figuren som vises i begynnelsen, representerer den blå kurven den nøyaktige løsningen på differensiallikningen, og den røde representerer de påfølgende omtrentlige punktene oppnådd ved Euler-prosedyren.
Løst øvelser
Øvelse 1
Jeg) La differensiallikningen være:

Med startbetingelsen x = a = 0; Ytil= 1
Få en omtrentlig løsning på Eulers metode Y i koordinaten X = b = 0,5, og deler intervallet [a, b] i n = 5 deler.
Løsning

De numeriske resultatene er oppsummert som følger:

Fra hvor det konkluderes med at løsningen Y for verdien 0,5 er 1,4851.
Merk: for å utføre beregningene, Smath studio, gratis å bruke gratis program.
Øvelse 2
II) Fortsett med differensiallikningen fra øvelse I), finn den nøyaktige løsningen og sammenlign den med resultatet oppnådd ved Eulers metode. Finn feilen eller forskjellen mellom det nøyaktige og omtrentlige resultatet.
Løsning

Den eksakte løsningen er ikke veldig vanskelig å finne. Derivatet av funksjonen sin (x) er kjent for å være funksjonen cos (x). Derfor blir løsningen y (x):
y (x) = sin x + C
For at den opprinnelige tilstanden skal oppfylles og (0) = 1, må konstanten C være lik 1. Det nøyaktige resultatet blir deretter sammenlignet med det omtrentlige:
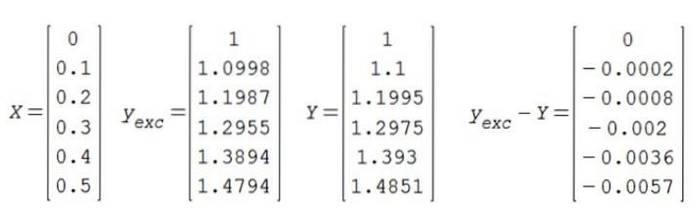
Det konkluderes med at tilnærmingen i det beregnede intervallet har tre signifikante presisjonstall.
Øvelse 3
III) Tenk på differensiallikningen og dens opprinnelige forhold gitt nedenfor:
y '(x) = - yto
Med den opprinnelige tilstanden x0 = 0; Y0 = 1
Bruk Eulers metode for å finne omtrentlige verdier av løsningen y (x) i intervallet x = [0, 1.5]. Bruk trinn h = 0,1.
Løsning
Eulers metode er veldig egnet til å brukes sammen med et regneark. I dette tilfellet vil vi bruke regnearket til geogebra, et gratis og gratis å bruke program.
Regnearket i figuren viser tre kolonner (A, B, C), den første er variabelen x , den andre kolonnen representerer variabelen Y, og den tredje kolonnen avledet Y '.
Rad 2 inneholder startverdiene for X, Y, Y ' .
Verditrinnet 0.1 er plassert i cellen med absolutt posisjon ($ D $ 4).
Den opprinnelige verdien av y0 er i celle B2, og y1 er i celle B3. For å beregne y1 formelen brukes:
Y1 = Yeller +(x1- xeller) f (xeller, Yeller) = ogeller + h f (xeller, Yeller)
Denne regnearkformelen vil være nummer B3: = B2 + $ D $ 4 * C3.
Tilsvarende vil y2 være i celle B4, og formelen er vist i følgende figur:
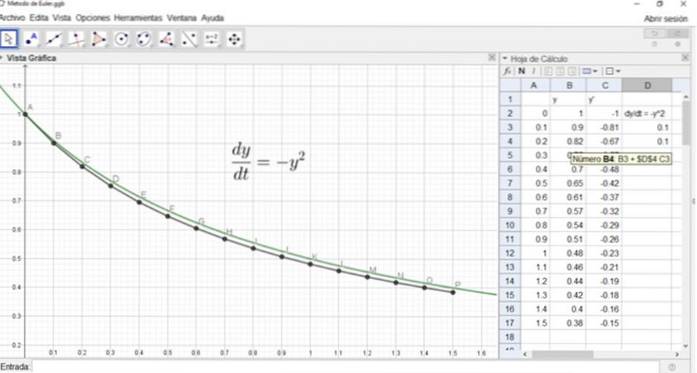
Figuren viser også grafen for den nøyaktige løsningen, og punktene A, B, ..., P for den omtrentlige løsningen etter Eulers metode.
Newtons dynamikk og Eulers metode
Klassisk dynamikk ble utviklet av Isaac Newton (1643 - 1727). Den opprinnelige motivasjonen til Leonard Euler (1707 - 1783) for å utvikle sin metode, var nettopp å løse ligningen til Newtons andre lov i forskjellige fysiske situasjoner..
Newtons andre lov uttrykkes vanligvis som en differensialligning av andre grad:

Hvor x representerer posisjonen til et objekt for øyeblikket t. Nevnte objekt har en masse m og blir utsatt for en styrke F. Funksjonen F er relatert til kraft og masse som følger:


For å anvende Eulers metode kreves de innledende verdiene for tiden t, hastighet v og posisjon x.
Den følgende tabellen forklarer hvordan man starter fra startverdiene t1, v1, x1, en tilnærming av hastigheten v2 og posisjonen x2, for øyeblikket t2 = t1 + Δt, der Δt representerer en liten økning og tilsvarer trinnet i metoden til Euler.

Øvelse 4
IV) Et av de grunnleggende problemene i mekanikken er en masseblokk M bundet til en fjær (eller fjær) med elastisk konstant K.
Newtons andre lov for dette problemet ville se slik ut:
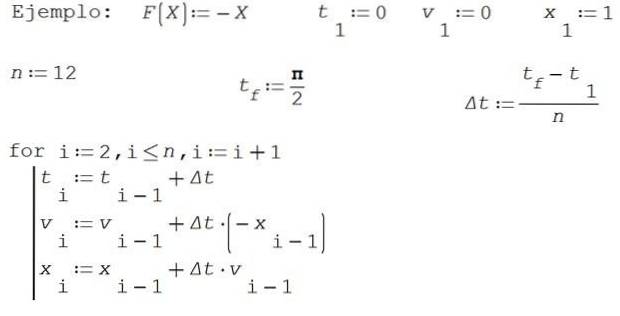
I dette eksemplet tar vi for enkelhets skyld M = 1 og K = 1. Finn omtrentlige løsninger for posisjonering x og fart v etter Eulers metode på tidsintervallet [0, π / 2] som deler opp intervallet i 12 deler.
Ta 0 som første øyeblikk, starthastighet 0 og utgangsposisjon 1.
Løsning
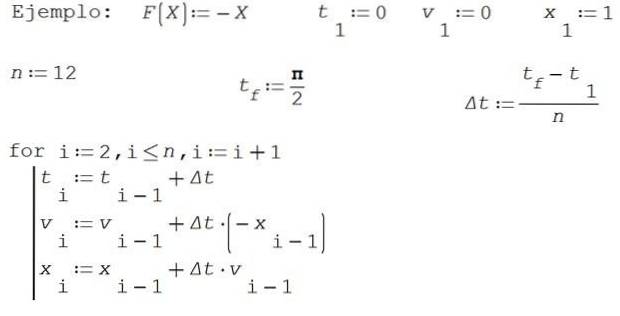
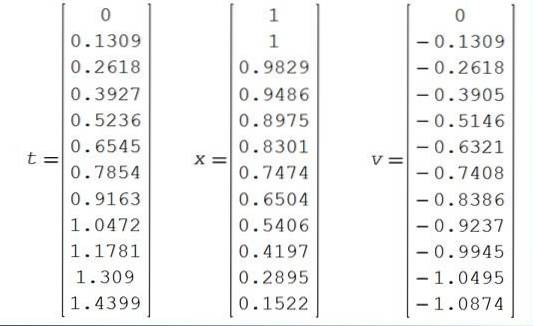
De numeriske resultatene er vist i følgende tabell:
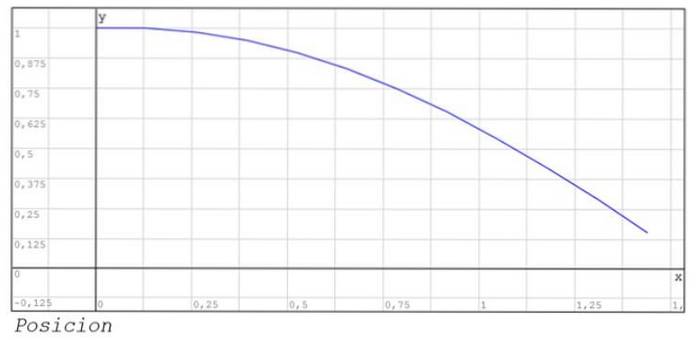
Grafene over posisjon og hastighet mellom øyeblikk 0 og 1.44 er også vist..
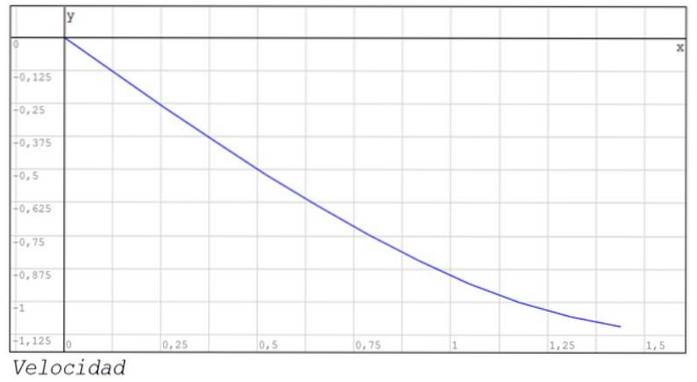
Foreslåtte øvelser for hjemmet
Øvelse 1
Bruk et regneark til å bestemme en omtrentlig løsning ved å bruke Eulers metode for differensiallikningen:
y '= - Exp (-y) med startbetingelsene x = 0, y = -1 i intervallet x = [0, 1]
Start med et 0,1 trinn. Plott resultatet.
Øvelse 2
Bruk et regneark til å finne numeriske løsninger på følgende kvadratiske ligning, der y er en funksjon av den uavhengige variabelen t.
y "= - 1 / y² med utgangsbetingelsen t = 0; y (0) = 0,5; y '(0) = 0
Finn løsningen på intervallet [0,5; 1.0] ved hjelp av et trinn på 0,05.
Plott resultatet: y vs t; y 'vs t
Referanser
- Eurlers metode Hentet fra wikipedia.org
- Euler-løser. Hentet fra en.smath.com



Ingen har kommentert denne artikkelen ennå.