
Dobbel prøvetaking


Hva er dobbel prøvetaking?
De dobbel prøvetaking er en teknikk som brukes i inferensiell statistikk når du vil vite mer detaljer og sikkerhet om en bestemt variabel, som kjennetegner en viss populasjon.
Den andre populasjonsprøven utføres vanligvis etter at en første prøve er tatt og analysert, hvis analyse ikke ga en statistisk signifikant konklusjon på noen av studievariablene..
Av denne grunn er dobbelt utvalg i statistikk også kjent som totrinns prøvetaking. Nytten av den andre prøven er at den hjelper til med større presisjon å bestemme estimeringen av forhold og regresjoner av en viss hjelpevariabel, som oppstår i lys av analysen av en første prøve..
En annen bruk som er gitt for dobbel prøvetaking er å samle inn informasjon for å utføre en prøvetaking etter lag..
Eksempler
Ulike situasjoner der dobbelt prøvetaking er berettiget, vil bli beskrevet nedenfor..
Kvalitetskontroll i produksjon av deler
Metoden med dobbelt prøvetaking brukes ofte i industriell kvalitetskontroll og gjøres vanligvis i to faser..
Anta for eksempel en industriell maskin som lager visse deler. Uansett hvor mye maskinen er justert, er ingen deler identiske med en annen, siden det kan forekomme små variasjoner i dimensjoner og vekt. Det handler om å avgjøre om et parti med deler produsert av maskinen oppfyller toleranskriteriene for at det skal aksepteres eller avvises..
Først tas et tilfeldig utvalg av brikker som du vil sjekke om en av variablene, for eksempel lengden på brikken, er innenfor toleranse.
I tilfelle at den gjennomsnittlige lengden er under eller over den ønskede toleranse for nevnte variabel, i denne første prøven, blir det utledet at partiet er mangelfullt og det må kastes. I dette tilfellet er det ikke nødvendig med nye prøver.
Omvendt, hvis gjennomsnittsverdien er innenfor toleranseområdet, men standardavviket til prøven er stort nok til at tillegg eller subtraksjon av gjennomsnittsverdien faller utenfor området, må en andre større prøve samles inn..
Denne andre prøven må inkludere den opprinnelige prøven for å gjøre om beregningene og dermed kunne ta en endelig beslutning om den undersøkte variabelen. På denne måten kan det være kjent om batchen er defekt eller ikke.
Lavere prøvetakingskostnader
Ved mange anledninger er informasjonen om en av variablene som skal studeres vanskelig tilgjengelig. Men det kan være en hjelpevariabel lettere for datainnsamling.
I dette tilfellet blir det tatt to prøver, en stor for hjelpevariabelen, billigere og en mindre prøve, inneholdt i den større prøven av den dyreste variabelen..
Denne metoden er anvendbar når det blir bestemt at det er en sammenheng mellom begge variablene, som generelt er et proporsjonalt forhold..
Et eksempel på denne situasjonen vises i skogvitenskap, der det er ønskelig å bestemme prosentandelen av trær som er berørt av en parasittisk plante (ringorm)..
Ettersom dette er svært omfattende regioner og vanskelig tilgjengelige, er det ikke mulig å studere den totale bestanden av trær i tid og kostnader. Disse trinnene følges deretter:
Trinn 1: ta prøver
En foreløpig prøvetaking vil bestå av bruk av luftfotografering, og skogen er delt inn i mye. Herfra blir noen få partier valgt tilfeldig, og det blir estimert, ved å analysere bildene av de utvalgte partiene, hvor mange trær som påvirkes av ringorm, siden fargen på trærne påvirkes av parasitten..
Trinn 2: feltarbeid
Men den fotografiske analysen kan være upresis, så noen få batcher av den første prøven blir valgt, helst tilfeldig, for å gjøre feltarbeid..
Trinn 3: sammenligning
Feltresultatet blir deretter sammenlignet med det fotografiske for avlytting av de to settene. Denne sammenligningen kan for eksempel utføres ved å lage en graf der den horisontale aksen er verdien oppnådd for hver batch gjennom fotografering og på den vertikale aksen verdien som oppnås per batch gjennom feltarbeid..
Denne grafiske metoden gjør det mulig å visuelt identifisere hvorvidt det er en sammenheng mellom begge resultatene, og å bestemme proporsjonalitetskoeffisienten eller forholdet mellom begge prøvene gjennom en regresjonsanalyse..
Etter den største prøven, det vil si fotografiprøven, blir gjennomsnittsverdien av infiserte trær og deres standardavvik tatt. Men siden proporsjonalitetskoeffisienten og feilen med feltprøvene ble bestemt, er det mulig å korrigere resultatet av den større prøven (den fotografiske).
Dette resultatet kan deretter ekstrapoleres til hele trepopulasjonen.
Fordeler og ulemper ved dobbel prøvetaking
I eksemplene som er beskrevet er kostnadsfordelen tydelig, siden det å erstatte en lett tilgjengelig variabel med en annen som er vanskelig tilgjengelig, sparer tid og penger..
En ulempe er at det i tilfelle dobbelt prøvetaking for kvalitetskontroll er en risiko for å gå gjennom gode partier med produkter som er utenfor toleranse..
Trening
Vi vil estimere antall syke trær i en 162 hektar stor skog. Siden skogen er veldig omfattende, er den delt inn i 100 pakker av samme område. 18 tomter er tilfeldig valgt, og ved hjelp av en fotografisk undersøkelse anslås det at det i disse 18 tomtene er 8,5 syke trær med en standardfeil på pluss minus 4,5 trær.
Fra disse 18 tomtene er det valgt tilfeldig 8 tomter der feltstudien utføres. For disse åtte tomtene viser den fotografiske studien 10 syke trær med en feil på pluss minus 5,3 trær..
På den annen side viser feltstudien for de samme åtte tomtene 12,4 syke trær med en feil på pluss minus 6,3 trær.
Det spør:
- a) Bestem proporsjonalitetskoeffisienten mellom feltstudien ved lineær regresjon.
- b) Beregn antall syke trær ved hjelp av fotografisk metode i hundre tomter.
- c) Bruk korreksjonen med oppnådd proporsjonalitetskoeffisient, for å estimere det virkelige antall syke trær i hele skogen.
Løsning
En graf er laget av antall trær per fotografisk antall vs feltantall for de åtte partiene som er valgt for begge studiene..
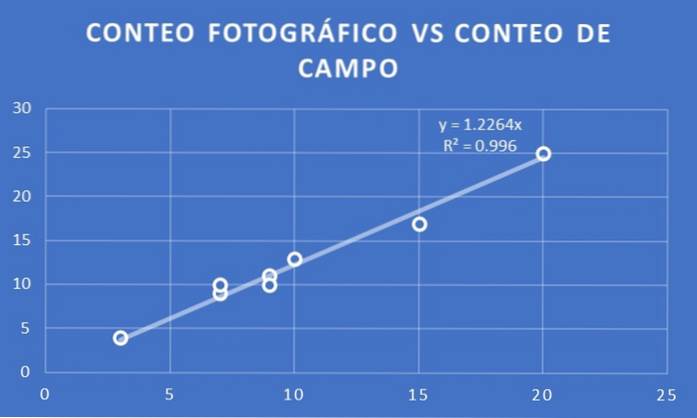
En trendlinje er montert og hellingen bestemt. I dette tilfellet oppnås det at proporsjonalitetskoeffisienten er 1,23. Det vil si at hvis X er antallet per fotografisk antall, anslås det at feltantallet vil være Y = 1,23 X.
Antall syke trær i henhold til fotografisk antall i de 18 utvalgte partiene vil være:
18 x 8,5 = 153
Men siden hele skogen ble delt inn i 100 tomter i samme område, er antallet syke trær som er estimert etter den fotografiske metoden: (100/18) x 153 = 850.
Korreksjonsfaktoren oppnådd fra sammenligningen mellom feltstudiet og fotografisk studie er nå brukt:
Anslått faktisk antall syke trær i skogen = 1,23 x 850 = 1046.
Referanser
- Dobbel prøvetaking for forholdsestimering, PennState College. Gjenopprettet fra psu.edu
- Dobbel, flere og sekvensiell prøvetaking, NC State University. Gjenopprettet fra ncsu.edu
- Enkel tilfeldig prøvetaking. Gjenopprettet fra investopedia.com
- Hva er dobbel prøvetaking? Gjenopprettet fra: nist.gov
- Prøvetaking. Gjenopprettet fra: en.wikipedia.org
- Flertrinns prøvetaking. Gjenopprettet fra: en.wikipedia.org



Ingen har kommentert denne artikkelen ennå.