Innskrevet vinkel på en sirkeldefinisjon, teoremer, eksempler

De innskrevet vinkel på en sirkel Det er et som har toppunktet på omkretsen, og dets stråler er hemmelige eller tangerende for det. Som en konsekvens vil den innskrevne vinkelen alltid være konveks eller flat..

I figur 1 er flere vinkler angitt i deres respektive omkrets representert. Vinkelen ∠EDF er innskrevet ved å ha toppunktet D på omkretsen og de to strålene [DE) og [DF) som krysser omkretsen. 

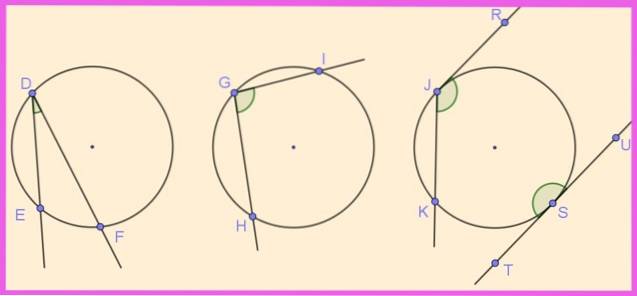
Tilsvarende er vinkelen ∠HGI innskrevet, da den har toppunktet på omkretsen og sidene er skille til den.

Vinklene ∠KJR og ∠UST er også innskrevet på omkretsen. Den første har en sekant side og den andre tangerer, mens den andre har sine to sider som tangerer omkretsen, og danner en plan innskrevet vinkel (180º).

Noen forfattere kaller den halvinnskrevne vinkelen som en av sidene har tangens til omkretsen, men i denne artikkelen regnes den som innskrevet..

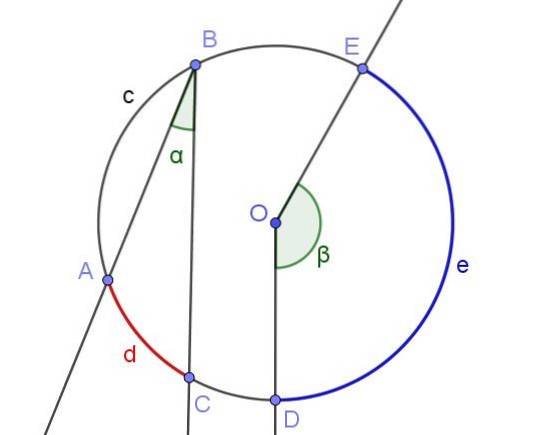
Hver innskrevet vinkel definerer eller undertrykker en bue assosiert med den. For eksempel undertegner vinkelen ∠ABC i figur 2 buen A⌒C med lengden d.

Den samme figuren viser vinkelen ∠DOE, som ikke er innskrevet i omkretsen fordi toppunktet ikke har omkretsen, men i sentrum O.

Artikkelindeks

• 1 Sentral vinkel
• 2 teoremer
  • 2.1 - Teorem 1 (innskrevet vinkel og sentral vinkel)
  • 2.2 - Teorem 2
  • 2.3 - Teorem 3
• 3 eksempler
  • 3.1 - Eksempel 1
  • 3.2 - Eksempel 2
• 4 Referanser

Sentral vinkel

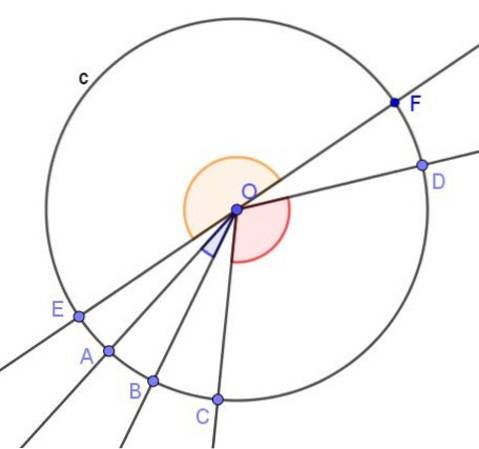
I tillegg til den innskrevne vinkelen, i en omkrets sentral vinkel, som er den som har toppunktet i sentrum av omkretsen og hvis sider krysser omkretsen.

Tiltaket i radianer av en sentral vinkel er kvotienten mellom den underliggende buen, det vil si omkretsbuen mellom sidene av vinkelen og radiusen av omkretsen.

Hvis omkretsen er enhetlig (av radius 1), er lengden på buen i de samme radienhetene mål for vinkelen i radianer.

Og når det kreves vinkelmåling i grader, multipliseres tiltaket i radianer med faktoren 180º / π.

Vinkelmåleinstrumenter bruker alltid en sentral vinkel, og lengden på buen som er understreket av den er direkte kalibrert i grader. Dette betyr at når en vinkel måles, i bakgrunnen, måles lengden på buen som er undertrykket av den sentrale vinkelen.

Setninger

- Theorem 1 (Inscribed Angle and Central Angle)

Mål på en innskrevet vinkel er halvparten av målet på den sentrale vinkelen, hvis begge vinklene understreker den samme buen.

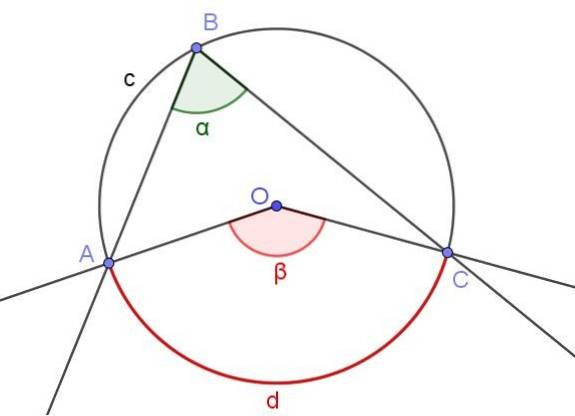
I figur 4 er det vist to vinkler ∠ABC og ∠AOC, som skjærer den samme bue av omkrets A⌒C.

Hvis målingen på den innskrevne vinkelen er α, er målingen β av den sentrale vinkelen dobbelt så stor som målingen for den innskrevne vinkelen (β = 2 α) fordi begge understreker den samme målebuen d.

Demonstrasjon 1a

For å bevise setning 1, begynner vi med å vise flere spesielle tilfeller, til vi når den generelle saken.

Anta en innskrevet vinkel der den ene siden går gjennom sentrum av omkretsen, som vist i figur 5.

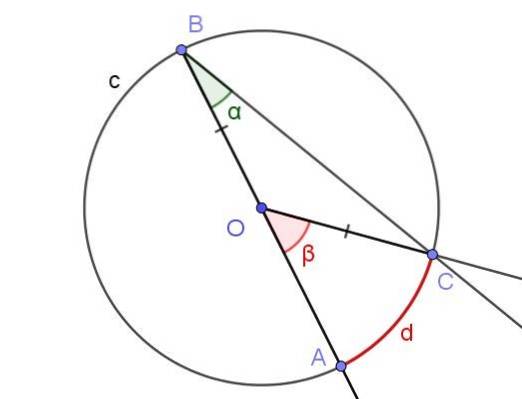
I dette tilfellet dannes den likebenede trekanten COB, siden [OC] = [OB].

I en likestilt trekant er vinklene ved siden av basen like, derfor ∠BCO = ∠ABC = α. På den annen side ∠COB = 180º - β.

Tatt i betraktning summen av de indre vinklene til trekanten COB, har vi:

α + α + (180 º - β) = 180 º

Fra hvilket det følger at 2 α = β, eller hva som tilsvarer: α = β / 2. Dette sammenfaller med det som setning 1 sier: målet for den innskrevne vinkelen er halvparten av den sentrale vinkelen, hvis begge vinklene underlegger samme akkord [AC].

Demonstrasjon 1b

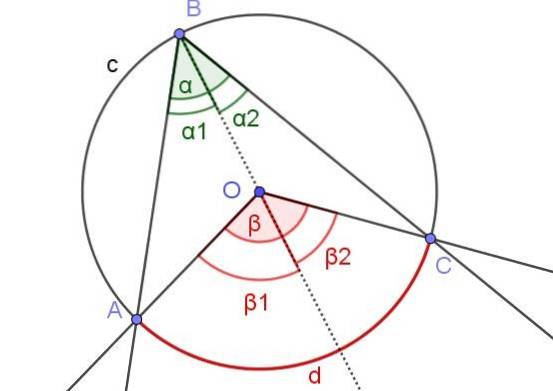
I dette tilfellet har vi en innskrevet vinkel ∠ABC, der sentrum O av omkretsen er innenfor vinkelen.

For å bevise teorem 1 i dette tilfellet tegnes hjelpestrålen [BO] slik at vi har to innskrevne vinkler ∠ABO og ∠OBC ved siden av strålen.

På samme måte har vi de sentrale vinklene β₁ og β_to ved siden av nevnte stråle. På denne måten har vi den samme situasjonen som i bevis 1a, så det kan sies at α_to = β_to / 2 og α₁ = β₁ /to. Siden α = α₁ + α_to og β = β₁ + β_to derfor følger det at α = α₁ + α_to = β₁ / 2 + β_to / 2 = (β₁ + β_to) / 2 = β / 2.

Avslutningsvis α = β / 2, som oppfyller setning 1.

- Setning 2

Hvis to eller flere innskrevne vinkler har samme bue, har de samme mål.

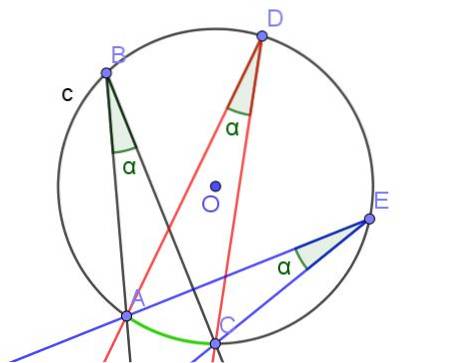
- Setning 3

De innskrevne vinklene som underordner akkorder av samme mål er like.

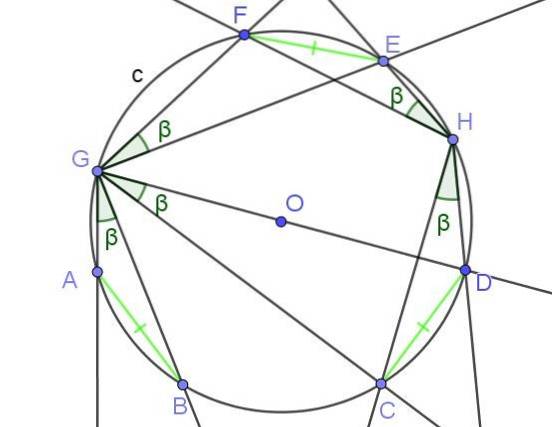
Eksempler

- Eksempel 1

Vis at den innskrevne vinkelen som understreker diameteren er en rett vinkel.

Løsning

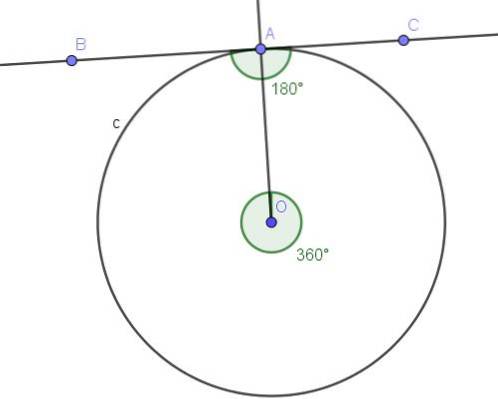
Den sentrale vinkelen ∠AOB assosiert med diameteren er en plan vinkel, hvis mål er 180 º.

I henhold til teorem 1 har hver vinkel som er innskrevet i omkretsen som legger samme akkord (i dette tilfellet diameteren), som mål halvparten av den midtre vinkelen som legger samme akkord, som for vårt eksempel er 180º / 2 = 90º.

- Eksempel 2

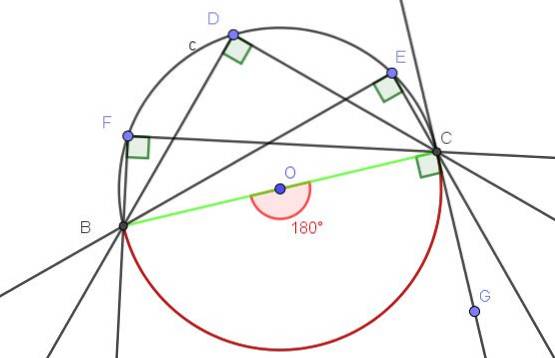
Linjen (BC) som tangerer A til omkretsen C, bestemmer den innskrevne vinkelen ∠BAC (se figur 10).

Bekreft at setning 1 av de innskrevne vinklene er oppfylt.

Løsning

Vinkelen ∠BAC er innskrevet fordi toppunktet er på omkretsen, og sidene [AB) og [AC] er tangent til omkretsen, slik at definisjonen av innskrevet vinkel er oppfylt.

På den annen side underkaster den innskrevne vinkelen ∠BAC buen A, A, som er hele omkretsen. Den sentrale vinkelen som legger buen A⌒A, er en konveks vinkel hvis mål er full vinkel (360º).

Den innskrevne vinkelen som legger hele buen, måler halvparten av den tilhørende sentrale vinkelen, det vil si ∠BAC = 360º / 2 = 180º.

Med alt det ovennevnte er det bekreftet at denne spesielle saken oppfyller setning 1.

Referanser

1. Baldor. (1973). Geometri og trigonometri. Mellomamerikansk kulturredaksjon.
2. E. A. (2003). Element av geometri: med øvelser og geometri av kompasset. University of Medellin.
3. Geometri 1. ESO. Vinkler på omkretsen. Gjenopprettet fra: edu.xunta.es/
4. All vitenskap. Foreslåtte øvelser av vinkler i omkretsen. Gjenopprettet fra: francesphysics.blogspot.com
5. Wikipedia. Innskrevet vinkel. Gjenopprettet fra: es.wikipedia.com