Supplerende vinkler hva er de, beregning, eksempler, øvelser

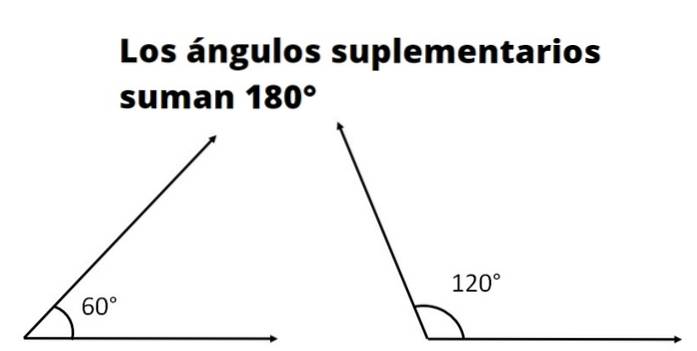
To eller flere er det tilleggsvinkler hvis summen av målene tilsvarer målet for en rett vinkel. Mål på en rett vinkel, også kalt en plan vinkel, i grader er 180 º og i radianer er det π.

For eksempel finner vi at de tre innvendige vinklene til en trekant er supplerende, siden summen av deres mål er 180º. Tre vinkler er vist i figur 1. Av det ovenstående følger at α og β er supplerende, siden de ligger ved siden av og summen fullfører en rett vinkel.

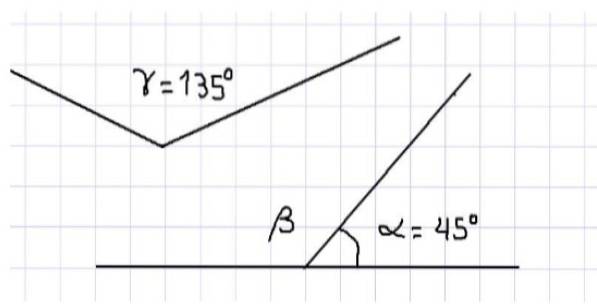
Også i samme figur har vi vinklene α og γ som også er supplerende, fordi summen av deres mål er lik målene for en plan vinkel, det vil si 180º. Det kan ikke sies at vinklene β og γ er supplerende fordi, da begge vinklene er stumpe, er deres mål større enn 90 º og derfor overstiger summen 180 º.

På den annen side kan det fastslås at målingen på vinkelen β er lik målingen på vinkelen γ, siden hvis β er supplerende til α og γ er supplerende til α, så er β = γ = 135º.

Artikkelindeks

• 1 Eksempler
  • 1.1 Eksempel A
  • 1.2 Eksempel B
  • 1.3 Eksempel C
  • 1.4 Eksempel D
  • 1.5 Eksempel E
  • 1.6 Eksempel F
• 2 Øvelser
  • 2.1 - Øvelse I
  • 2.2 - Øvelse II
  • 2.3 - Øvelse III
• 3 Supplerende vinkler i to paralleller kuttet av en sekant
  • 3.1 - Øvelse IV
• 4 Referanser

Eksempler

I de følgende eksemplene blir det bedt om å finne de ukjente vinklene, angitt med spørsmålstegn i figur 2. De spenner fra de enkleste eksemplene til noen litt mer forseggjorte at leseren skal være mer forsiktig.

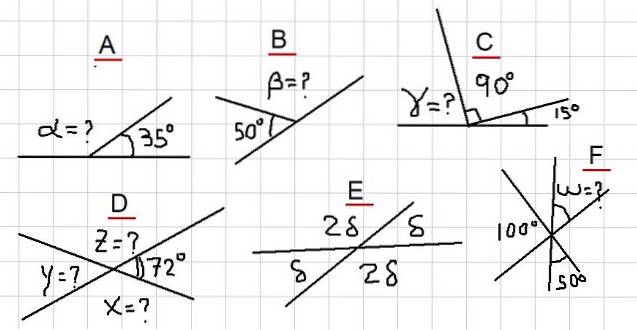
Eksempel A

I figuren har vi at tilstøtende vinkler α og 35 º legger opp til en plan vinkel. Det vil si α + 35º = 180º og derfor er det sant at: α = 180º- 35º = 145º.

Eksempel B

Siden β er supplerende med vinkelen på 50º, følger det at β = 180º - 50º = 130º.

Eksempel C

Fra figur 2C observeres følgende sum: γ + 90º + 15º = 180º. Det vil si at γ er supplerende med vinkelen 105º = 90º + 15º. Det ble da konkludert med at: 

γ = 180 º - 105 º = 75 º

Eksempel D

Siden X er supplement til 72º, følger det at X = 180º - 72º = 108º. Videre er Y supplerende med X, så Y = 180º - 108º = 72º.

Og til slutt er Z supplerende med 72º, derfor Z = 180º - 72º = 108º.

Eksempel E

Vinklene δ og 2 δ er supplerende, derfor δ + 2 δ = 180 º. Noe som betyr at 3δ = 180º, og dette igjen lar oss skrive: δ = 180º / 3 = 60º.

Eksempel F

Hvis vi kaller vinkelen mellom 100º og 50º U, er U supplerende til dem, fordi det observeres at summen deres fullfører en plan vinkel.

Det følger umiddelbart at U = 150º. Siden U er motsatt av toppunktet til W, så er W = U = 150º.

Opplæring

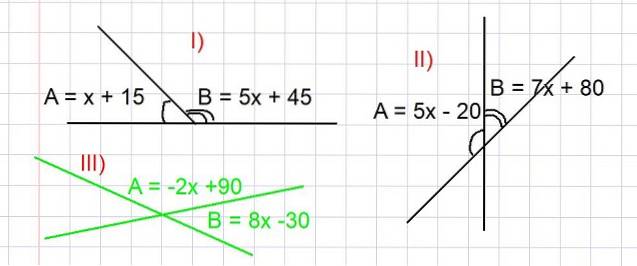
Tre øvelser er foreslått nedenfor, i alle må verdien av vinklene A og B i grader være funnet, slik at forholdene vist i figur 3. Oppfylles. Begrepet supplerende vinkler brukes til å løse dem alle..

- Øvelse I

Bestem verdiene til vinklene A og B fra del I) i figur 3.

Løsning

A og B er supplerende, hvorfra vi har at A + B = 180 grader, så er uttrykket for A og B erstattet som en funksjon av x, slik det ser ut på bildet:

(x + 15) + (5x + 45) = 180

En lineær ligning av første ordre oppnås. For å løse det grupperes begrepene umiddelbart:

6 x + 60 = 180

Ved å dele begge medlemmene på 6 har vi:

x + 10 = 30

Og til slutt å løse, følger det at x er verdt 20º.

Nå må vi plugge inn verdien på x for å finne de valgte vinklene. Derfor er vinkelen A: A = 20 +15 = 35º.

Og for sin del er vinkel B B = 5 * 20 + 45 = 145º.

- Øvelse II

Finn verdiene til vinklene A og B fra del II) i figur 3.

Løsning

Siden A og B er supplerende vinkler, har vi at A + B = 180 grader. Ved å erstatte uttrykket for A og B som en funksjon av x gitt i del II) i figur 3, har vi:

(-2x + 90) + (8x - 30) = 180

Igjen oppnås en førstegradsligning, som vilkårene må være gruppert for:

6 x + 60 = 180

Ved å dele begge medlemmene på 6 har vi:

x + 10 = 30

Det følger av at x er verdt 20º.

Med andre ord, vinkelen A = -2 * 20 + 90 = 50º. Mens vinkel B = 8 * 20-30 = 130º.

- Øvelse III

Bestem verdiene til vinklene A og B fra del III) i figur 3 (i grønn farge).

Løsning

Siden A og B er supplerende vinkler, har vi at A + B = 180 grader. Vi må erstatte uttrykket for A og B som en funksjon av x gitt i figur 3, hvorfra vi har:

(5x - 20) + (7x + 80) = 180

12 x + 60 = 180

Ved å dele begge medlemmene med 12 for å løse verdien av x, har vi:

x + 5 = 15

Endelig er det funnet at x er verdt 10 grader.

Nå fortsetter vi å erstatte for å finne vinkelen A: A = 5 * 10 -20 = 30º. Og for vinkel B: B = 7 * 10 + 80 = 150º

Supplerende vinkler i to paralleller kuttet av en sekant

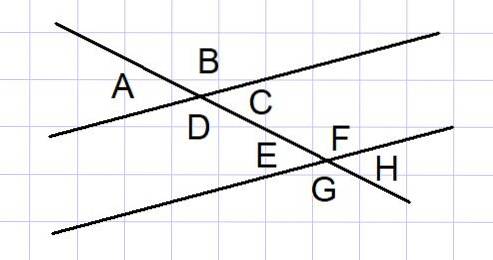
To parallelle linjer kuttet av en sekant er en vanlig geometrisk konstruksjon i noen problemer. Mellom slike linjer dannes 8 vinkler som vist i figur 4.

Av disse 8 vinklene er noen par vinkler supplerende, som vi viser nedenfor:

1. De utvendige vinklene A og B, og de utvendige vinklene G og H
2. Innvendige vinkler D og C, og innvendige vinkler E og F
3. De utvendige vinklene A og G, og de ytre vinklene B og H
4. Interiørvinklene D og E, og interiørene C og F

For fullstendighet er vinklene like hverandre også navngitt:

1. De interne vekslene: D = F og C = E
2. De eksterne alternerer: A = H og B = G
3. De tilsvarende: A = E og C = H
4. Motsetninger etter toppunkt A = C og E = H
5. De tilsvarende: B = F og D = G
6. Motsetninger etter toppunkt B = D og F = G

- Øvelse IV

Med henvisning til figur 4, som viser vinklene mellom to parallelle linjer kuttet av en sekant, bestem verdien av alle vinkler i radianer, vel vitende om at vinkelen A = π / 6 radianer.

Løsning

A og B er supplerende ytre vinkler, så B = π - A = π - π / 6 = 5π / 6

A = E = C = H = π / 6

B = F = D = G = 5π / 6

Referanser

1. Baldor, J. A. 1973. Plane and Space Geometry. Mellomamerikansk kultur. 
2. Matematiske lover og formler. Vinkelmålesystemer. Gjenopprettet fra: ingemecanica.com.
3. Wentworth, G. Plane Geometry. Gjenopprettet fra: gutenberg.org.
4. Wikipedia. Supplerende vinkler. Gjenopprettet fra: es.wikipedia.com
5. Wikipedia. Transportør. Gjenopprettet fra: es.wikipedia.com
6. Zapata F. Goniómetro: historie, deler, drift. Gjenopprettet fra: lifeder.com