De nkvantetall brukes til å beskrive kvantetilstanden til elektronene i atomet og stammer fra løsningen av Schrödinger-ligningen for det enkleste av alle: hydrogen.
Schrödinger-ligningen er en differensialligning, hvis løsninger er bølgefunksjoner og er betegnet med den greske bokstaven ψ. Uendelige løsninger kan foreslås, og kvadratet er lik sannsynligheten for å finne elektronet i et lite område av rommet, kalt orbital.
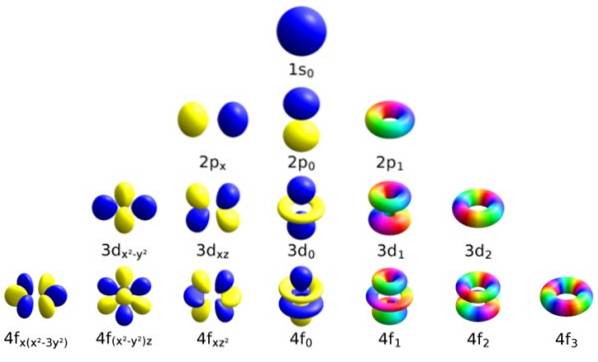
Hver bane har bestemte egenskaper som skiller den fra de andre, som energi, vinkelmoment og spinn, en helt kvanteegenskap for elektronet og som blant annet er ansvarlig for magnetiske effekter..
Måten å identifisere hver bane er å skille den med et sett med tall som beskriver det, og dette er nettopp kvantetallene:
-n: er hovedkvantetallet.
-ℓ: det azimutale kvantetallet.
-mℓ, er det magnetiske tallet.
-ms, spinnnummeret.
Artikkelindeks
Kvantetall brukes til å beskrive tilstanden til elektronene inne i atomet. Atommodellen der elektronet kretser rundt kjernen er unøyaktig, fordi den ikke er i samsvar med atomstabilitet eller med et stort antall observerte fysiske fenomener..
Derfor kom danske Niels Bohr (1885-1962) med et dristig forslag i 1913: elektronet kan bare finnes i visse stabile baner, hvis størrelse avhenger av et heltall kalt n.
Senere, i 1925, foreslo den også østerrikske fysikeren Erwin Schrödinger (1887-1961) en differensialligning i partielle derivater, hvis løsninger beskriver hydrogenatomet. De er bølgefunksjonene ψ nevnt i begynnelsen.
Denne differensialligningen inkluderer de tre romlige koordinatene pluss tid, men når dette ikke er inkludert, er løsningen av Schrödinger-ligningen analog med en stående bølge (en bølge som forplantes mellom visse grenser).
Den tidsuavhengige Schrödinger-ligningen løses i sfæriske koordinater, og løsningen skrives som produktet av tre funksjoner, en for hver romlige variabel. I dette koordinatsystemet, i stedet for å bruke koordinatene til de kartesiske aksene x, Y Y z koordinatene brukes r, θ Y φ. På denne måten:
ψ (r, θ, φ) = R (r) ⋅f (θ) ⋅g (φ)
Bølgefunksjonen er immateriell, men kvantemekanikken forteller oss at den kvadratiske amplituden:
| ψ (r, θ, φ) |to
Det vil si at modul eller absolutt verdi av bølgefunksjonen, i kvadrat, er et reelt tall som representerer sannsynligheten for å finne elektronet, i en bestemt region rundt punktet hvis koordinater er r, θ Y φ.
Og dette faktum er noe mer konkret og håndgripelig.
For å finne bølgefunksjonen, må du løse tre vanlige differensiallikninger, en for hver variabel r, θ Y φ.
Løsningene til hver ligning, som vil være funksjonene R (r), f (θ) og g (φ), inneholder de tre første kvantetallene som er nevnt.
Vi beskriver kort arten av hvert kvantetall nedenfor. De tre første, som tidligere nevnt, stammer fra løsningene i Schrödinger-ligningen.
Den fjerde utgaven ble lagt til av Paul Dirac (1902 - 1984) i 1928.
Det er betegnet med n og indikerer størrelsen på den tillatte bane, så vel som elektronens energi. Jo høyere verdi, jo lenger er elektronet fra kjernen, og energien vil også være høyere, men til gjengjeld reduserer den stabiliteten.
Dette tallet kommer fra funksjonen R (r), som er sannsynligheten for å finne elektronet på en viss avstand r av kjernen, som bestemmes av:
-Plancks konstant: h = 6,626 × 10 -3. 4 J.s
-Elektronmasse mog = 9,1 × 10-31 kg
-Elektronladning: e = 1,6 × 10-19 C.
-Elektrostatisk konstant: k = 9 × 10 9 N.mto/ Cto
Når n = 1 tilsvarer det Bohr-radiusen som er omtrent 5,3 × 10−11 m.
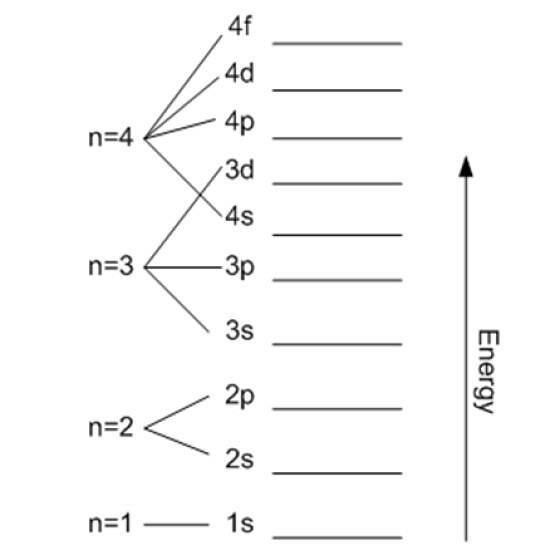
Med unntak av det første laget, er de andre delt inn i underlag eller undernivåer. Hvert skall har en energi i elektronvolt gitt av:
I teorien er det ingen øvre grense for n, men i praksis observeres det at den bare når n = 8. Lavest mulig energi tilsvarer n = 1 og er den for grunnleggende tilstand.
Betegnet med den kursive bokstaven ℓ, bestemmer dette tallet formen på orbitalene, ved å kvantifisere størrelsen på elektronets banevinkelmoment.
Det kan ta positive og heltallverdier mellom 0 og n-1, for eksempel:
-Når n = 1, så er ℓ = 0 og det er bare ett undernivå.
-Hvis n = 2, kan ℓ være lik 0 eller 1, så vi har to undernivåer.
-Og hvis n = 3, antar ℓ verdiene 0, 1 og 2 og det er 3 undernivåer.
Det kan fortsettes på denne måten på ubestemt tid, selv om som sagt før, i praksis n går opp til 8. Undernivåene er betegnet med bokstavene: s, s, d, F Y g og de øker i energi.
Dette tallet bestemmer orbitalens retning i rommet, og verdien avhenger av ℓ.
For en gitt ℓ er det (2ℓ + 1) heltallverdier på m ℓ, som tilsvarer de respektive orbitalene. Disse er:
-ℓ, (- ℓ + 1),… 0,… (+ ℓ -1), + ℓ.
Hvis n = 2, vet vi at ℓ = 0 og ℓ = 1, så m ℓ tar følgende verdier:
-For ℓ = 0: m ℓ = 0.
-For ℓ = 1: m ℓ = -1, m ℓ = 0, m ℓ = +1
Orbitale n = 2 har to undernivåer, den første med n = 2, ℓ = 0 og m ℓ = 0. Så har vi det andre delnivået: n = 2, ℓ = 1, med 3 orbitaler:
De tre orbitalene har samme energi, men ulik romlig orientering.
Når du løser Schrödinger-ligningen i tre dimensjoner, kommer tallene som allerede er beskrevet frem. Imidlertid observeres i hydrogen en enda finere struktur som disse tallene ikke er nok til å forklare.
Av denne grunn foreslo en annen fysiker, Wolfgang Pauli, i 1921 eksistensen av et fjerde tall: spinnnummeret ms, som tar verdier på + ½ eller -½.
Dette tallet beskriver en veldig viktig egenskap for elektronet, som er snurre rundt, ord som kommer fra engelsk snurre rundt (for å slå på seg selv). Og spinnet er i sin tur relatert til atomets magnetiske egenskaper.
En måte å forstå spinn på er å forestille seg at elektronet oppfører seg som en liten magnetisk dipol (en magnet med nord- og sørpoler), takket være en rotasjon rundt sin egen akse. Rotasjonen kan være i samme retning som med klokken, eller i motsatt retning.
Selv om Pauli foreslo eksistensen av dette nummeret, hadde resultatene av et eksperiment utført av Otto Stern og Walter Gerlach i 1922 allerede forventet det..
Disse forskerne klarte å dele en stråle av sølvatomer i to ved å bruke et ikke-ensartet magnetfelt.
Verdien av ms avhenger ikke av n, ℓ og m ℓ. I grafisk form representeres den av en pil: en pil opp indikerer en sving med urviseren og en nedoverpil indikerer en moturs sving.
Oppførselen til elektroner i atomet er oppsummert i Pauli-ekskluderingsprinsippet, som sier at to elektroner i et atom ikke kan eksistere i samme kvantetilstand..
Derfor må hvert elektron ha et annet sett med kvantetall n, ℓ, m ℓ og Ms.
Betydningen av kvantetall og dette prinsippet ligger i forståelsen av egenskapene til elementene i det periodiske systemet: elektroner er organisert i lag i henhold til n, og deretter i underlag i henhold til ℓ og resten av tallene.
Ingen har kommentert denne artikkelen ennå.