
Jevntall hvordan man identifiserer dem, eksempler, øvelser

De parnummer er alle de som kan deles nøyaktig med 2, for eksempel 0, 2, 4, 6, 8 10, 12, 14, 16, 18 ... Blant de negative tallene er det også par: -2, -4, - 6, - 8, -10 ...
Hvis vi ser nøye på tallene som følger 8 i rekkefølgen av positive tall: 10, 12, 14, 16 og 18, kan det sees at de ender på henholdsvis 0, 2, 4, 6 og 8. Med dette i bakhodet kan følgende partall tall konstrueres: 20, 22, 24, 26, 28, 30, 32, 34, 36, 38 ...
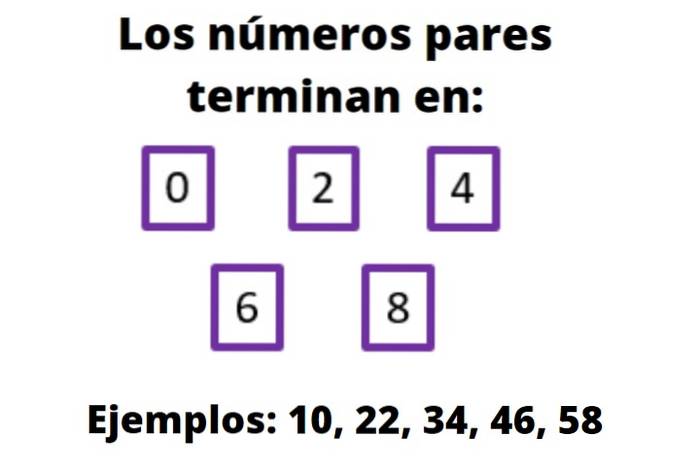
Det konkluderes med at for å identifisere et par, uansett hvor stort det er, eller hvis det har et negativt tegn, se på tallet der det ender. Hvis dette er 0, 2, 4, 6 eller 8, er vi i nærvær av et partall. For eksempel: 1554, 3578, -105.962 og så videre.
Siden hvert partall er delbart med nøyaktig 2, kan vi oppnå et partall fra alle andre ganske enkelt ved å multiplisere med 2. Det følger at den generelle formen for et hvilket som helst partall er:
2n
Hvor n er et helt tall:… -2, -1, 1, 2, 3, 4, 5,…
Og hva skjer med tallene som er mellom parene, som 3, 5, 7 og mer?
Vel, det er de oddetall. På denne måten kan hele tall klassifiseres i disse to brede kategoriene: odde og jevne. Denne kvaliteten på tall kalles paritet.
Og som vi ser fra de numeriske sekvensene, er de jevne og oddene sammenflettet, det vil si hvis vi begynner med 0, som er jevn, så 1, som er merkelig, så 2, som er jevn, så 3, som er rart. og så videre.
Artikkelindeks
- 1 Eksempler på partall
- 2 Operasjoner og egenskaper for partall
- 3 Løst øvelser
- 3.1 - Øvelse 1
- 3.2 - Øvelse 2
- 3.3 - Øvelse 3
- 4 Referanser
Eksempler på partall
Så lenge det er hele mengder, kan noen av dem være jevne og finnes i naturen og i mange virkelige situasjoner. Hvis vi har en viss mengde med hvilke grupper på to som kan dannes, er den størrelsen jevn. For eksempel:
-Totalt er fingrene på hendene 10, som er et partall. Vi har også jevnt antall øyne, armer, ører, ben og føtter.
-Insekter har nesten alltid 2 par vinger, det vil si at de har 4 vinger totalt, de har også 3 par ben, totalt 6 ben og 2 antenner.
-Vi har 2 foreldre, 4 besteforeldre, 8 oldeforeldre, 16 oldeforeldre og så videre nedover slektstreet. Dette er alle partall.
-Det er blomster med et jevnt antall kronblader, inkludert noen tusenfryd som har opptil 34.

-En jury består vanligvis av 12 personer.
-Sport som tennis, boksing, gjerder, bryting, sjakk spilles mellom 2 personer. I tennis er det kamper mellom par.
-Et volleyballag består av 6 spillere på banen.
-Sjakkbrettet har 64 firkanter og 2 sett med brikker: hvitt og svart. Settet har 16 stykker kalt slik: konge, dronning, biskop, ridder og bonde, som alle har et jevnt antall stykker, bortsett fra kongen og dronningen som er unike. På denne måten har hver spiller 2 biskoper, 2 tårn, 2 riddere og 8 bønder..
Operasjoner og egenskaper for partall
Med de jevne tallene kan du utføre alle de kjente aritmetiske operasjonene: legge til, trekke fra, multiplisere, dele, forbedre og mer. Oppsummert kan alle tillatte operasjoner gjøres med heltallene, der partallene er en del.
Resultatene av disse operasjonene har imidlertid noen særegenheter. Merkbare ting som vi kan observere fra resultatene er følgende:
-Partallene er presentert ispedd mellom de merkelige, som vi så tidligere.
-Hver gang vi legger til to eller flere like tall, blir resultatet jevnt. La oss se:
2 + 18 + 44 + 4 = 68
-Men hvis vi legger til to tall, ett like og ett oddetall, er resultatet merkelig. For eksempel 2 + 3 = 5 eller 15 + 24 = 39.
-Ved å multiplisere to partall vil vi også få et partall. Det samme skjer hvis vi multipliserer et oddetall eller et partall. For å se det, la oss gjøre noen enkle operasjoner som:
Par x par: 28 x 52 = 1456
Odd x jevn: 12 x 33 = 396
I stedet er produktet av to oddetall alltid odde.
-Ethvert tall som løftes til en jevn kraft er positivt, uavhengig av tegnet på tallet:
to4 = 2 x 2 x 2 x 2 = 16
(-5)to = (-5) x (-5) = 25
(-3)4 = (-3) x (-3) x (-3) x (-3) = 81
-Ja til er et tall slik at tilto det er enda da til det er jevnt. La oss undersøke de første rutene for å se om de stammer fra partall:
4, 9,16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225 ...
Det er sant at: 2to = 4 og 2 er jevn; 16 = 4to, 36 = 6to og så.
I stedet er 25 kvadraten på 5, som er merkelig, 49 er kvadratet på 7, som også er merkelig.
-Resten mellom delingen av ett par og et annet par er også jevn. Hvis vi for eksempel deler 100 med 18, er kvotienten 5 og resten er 10.
Løst øvelser
- Øvelse 1
Identifiser hvilke som er like tall og hvilke som er rare:
12, 33, 46, 51, 69, 70, 82, 98, 100, 101, 121, 134, 145, 159, 162, 177, 183, 196.
Løsning
12, 46, 70, 82, 98, 100, 134, 162, 196.
- Øvelse 2
Tre jevne tall på rad legger opp til 324. Hva er tallene?
Løsning
La oss være et hvilket som helst nummer som vi vil kalle "n". Siden vi ikke vet om det er jevnt eller ikke, sørger vi for at det er med kriteriet gitt i begynnelsen, det som sier at et partall er av formen 2n.
Antallet påfølgende til 2n er 2n + 1, men det er rart, fordi vi vet at de er sammenflettet, så vi legger tilbake 1: 2n +2.
Og med dette er det tredje tallet: 2n + 4.
Nå som vi har de tre påfølgende partallene klare, legger vi dem til og tilsvarer summen til 324, slik utsagnet krever:
2n + 2n + 2 + 2n + 4 = 324
Vi legger til alle "2n" -termer, siden de er like, og også tallene til venstre for likestillingen:
6n + 6 = 324 → 6n = 318
n = 53
Men oppmerksomhet, n = 53 Det er ikke et partall og er ikke en del av tallene som problemet ber oss om. Uttalelsen sier at de er "tre partall på rad".
Egentlig er det første tallet vi ser etter: 2n = 2 x 53 = 106.
Den neste er 108 og den tredje er 110.
Hvis vi legger til de tre tallene, ser vi at 324 faktisk oppnås:
106 + 108 + 110 = 324
- Øvelse 3
Finn en formel for å oppnå det tjuende jevne naturlige tallet, fra 0 og finn dette tallet, og sjekk manuelt.
Løsning
Husk at 0 er det første partall, så kommer 2, deretter 4 og så sammenflettet, la oss tenke på en formel som lar oss få 0 fra et annet tall, en som også er naturlig.
Denne formelen kan være:
2n - 2, med n = 1, 2, 3, 4, 5 ... .
Med den får vi 0 ved å lage n = 1:
2.1 - 2 = 0
La oss nå lage n = 2 og få paret 2
2.2 - 2 = 2
Å ta n = 3 resulterer i par 4:
2.3 - 2 = 4
Til slutt lager n = 20:
- 20 - 2 = 40 - 2 = 38
Det tjuende paret er 38, og vi bekrefter det:
0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38
Kan leseren fortelle hva det hundre og femte partallet blir ved å bruke formelen?
Referanser
- Baldor, A. 1986. Aritmetikk. Codex-utgaver og distribusjoner.
- Matematikk er gøy. Jevne og oddetall. Gjenopprettet fra mathisfun.com.
- Matematikkverksted. Jevnlig dualitet. Gjenopprettet fra: ehu.eus.
- Wikipedia. Paritet på null. Gjenopprettet fra: es.wikipedia.org.
- Wikipedia. Paritet. Gjenopprettet fra: en.wikipedia.org.


Ingen har kommentert denne artikkelen ennå.