Perfekte tall hvordan du kan identifisere dem og eksempler

EN perfekt tall er et naturlig tall slik at summen av delene er den samme som tallet. Selve tallet kan selvsagt ikke inkluderes mellom delerne.

Et av de enkleste eksemplene på et perfekt tall er 6, siden dets delere er: 1, 2 og 3. Hvis vi legger til delene, får vi: 1 + 2 + 3 = 6.

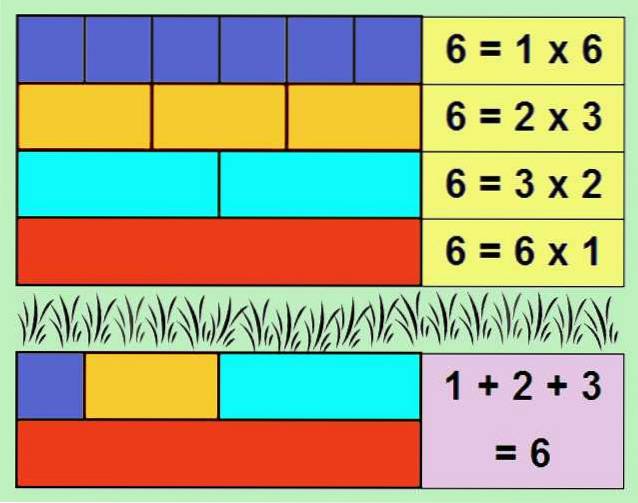
Summen av delene til et helt tall, ikke inkludert selve tallet, kalles alikvot. Derfor er et perfekt tall lik alikvoten.

Men hvis selve tallet er inkludert i summen av delere av et tall, vil et perfekt tall være ett som summen av alle dets delere delt med 2 er lik selve tallet..

Artikkelindeks

• 1 Historie
• 2 Egenskaper med perfekte tall
  • 2.1 Euclids formel og kriterium
  • 2.2 Det største kjente perfekte tallet
  • 2.3 Et perfekt nummer er venner med seg selv
• 3 Eksempler på perfekte tall
• 4 Øvelser
  • 4.1 - Øvelse 1
  • 4.2 - Øvelse 2
  • 4.3 - Øvelse 3
  • 4.4 - Øvelse 4
• 5 Referanser

Historie

Antikens matematikere, særlig grekerne, la stor vekt på perfekte tall og tilskrev dem guddommelige egenskaper..

For eksempel bekreftet Philo av Alexandria, mot det første århundre, at 6 og 28 er perfekte tall som sammenfaller med de seks dagene verdens skapelse og de tjueto dagene det tar for månen å gå rundt jorden..

Perfekte tall er også til stede i naturen, for eksempel på nordpolen til Saturn vises også det perfekte tallet 6, en sekskantformet virvel funnet av Cassini-sonden og som forskere har fascinert.. 

Bikakene til biene har celler i sekskantet form, det vil si med 6 sider. Det er vist at polygonet med det perfekte tallet 6 er det som tillater maksimering av antall celler i bikuben, med et minimum av voks for utarbeidelsen..

Egenskaper med perfekte tall

Summen av alle delere av et naturlig tall n er betegnet med σ (n). I et perfekt tall er det tilfreds med at: σ (n) = 2n.

Euclids formel og kriterier

Euclid oppdaget en formel og et kriterium som gjør det mulig å finne de perfekte tallene. Denne formelen er:

to^(n-1) (toⁿ -1)

Imidlertid vil tallet som genereres av formelen bare være perfekt når faktoren (2ⁿ -1) være en fetter.

La oss se hvordan de første perfekte tallene genereres:

Hvis n = 2, sitter vi igjen med 2¹ (to^to - 1) = 2 x 3 = 6 som vi allerede har sett er perfekt.

Når n = 3 har vi 2^to (to³ - 1) = 4 x 7 = 28, som også er perfekt, som det er detaljert verifisert i eksempel 1.

La oss se hva som skjer med n = 4. Når vi bytter ut i Euclids formel, har vi:

to³ (to⁴ - 1) = 8 x 15 = 120

Det kan verifiseres at dette tallet ikke er perfekt, som vist i detalj i eksempel 3. Dette strider ikke mot Euclids kriterium, siden 15 ikke er prime, et nødvendig krav for at resultatet skal være et perfekt tall.

La oss nå se hva som skjer når n = 5. Ved å bruke formelen har vi:

to⁴ (to⁵ - 1) = 16 x 31 = 496

Siden 31 er et primtall, må tallet 496 være perfekt, i henhold til Euclids kriterier. I eksempel 4 er det vist i detalj at det faktisk er.

Primtall som har skjema 2^s - 1 kalles fettere til Mersenne, etter munken Marin Mersenne, som studerte primtall og perfekte tall tilbake på 1600-tallet..

Senere på 1700-tallet viste Leonhard Euler at alle perfekte tall generert av Euclids formel er jevne.

Til dags dato er det ikke funnet noe perfekt som er rart.

Det største perfekte nummeret

Til dags dato er 51 perfekte tall kjent, alle generert av formelen og Euclids kriterium. Dette tallet ble oppnådd når den større Mersenne-fetteren ble funnet, som er: (2^82589933 - 1).

Det perfekte tallet # 51 er (2^82589933) x (2^82589933 - 1) og har 49724095 sifre.

Et perfekt nummer er venner med seg selv

I tallteori sies det at to tall er venner når summen av delere av en, ikke inkludert selve tallet, er lik det andre tallet og omvendt.

Leseren kan verifisere at summen av delere på 220, ikke inkludert 220, er 284. På den annen side er summen av delere på 284, ikke inkludert 284, lik 220. Derfor er tallet på nummer 220 og 284 venner.

Fra dette synspunktet er et perfekt nummer venner med seg selv..

Eksempler på perfekte tall

De første åtte perfekte tallene er listet opp nedenfor:

6

28

496

8128

33550336

8589869056

137438691328

2305843008139952128

Opplæring

I de følgende øvelsene vil det være nødvendig å beregne delene til et tall, for deretter å legge dem til og verifisere om tallet er et perfekt tall eller ikke..

Derfor, før vi nærmer oss øvelsene, vil vi gjennomgå konseptet og vise hvordan de beregnes..

Til å begynne med må du huske at tall kan være primtall (når de bare kan deles nøyaktig med seg selv og 1) eller sammensatte (når de kan spaltes som et produkt av primtall).

For et sammensatt tall N har vi:

N = aⁿ . b^m. c^s ... r^k 

Hvor a, b, c… r er primtall og n, m, p ... k er eksponenter som tilhører de naturlige tallene, som kan være fra 1 og utover.

Når det gjelder disse eksponentene, er det en formel for å vite hvor mange delere tallet N har, selv om det ikke forteller oss hva dette er. La C være denne mengden, så:

C = (n +1) (m + 1) (p +1) ... (k + 1)

Å dekomponere tallet N som et produkt av primtall og vite hvor mange delere det har, både primtall og ikke-primtall, vil hjelpe oss med å bestemme hva disse delerne er..

Når du har alle sammen, bortsett fra den siste som ikke kreves i summen, kan du sjekke om det er et perfekt tall eller ikke.

- Øvelse 1

Bekreft at tallet 28 er perfekt.

Løsning

Det første vil være å dekomponere tallet i dets viktigste faktorer.

28 | 2
14 | 2
07 | 7
01 | 1

Delingene er: 1, 2, 4, 7, 14 og 28. Hvis vi utelukker 28, gir summen av delene:

1 + 2 + 4 + 7 + 14 = 3 + 4 + 7 + 14 = 7 + 7 + 14 = 14 + 14 = 28

Derfor er 28 et perfekt tall.

Videre er summen av alle delene 28 + 28, så regelen σ (28) = 2 x 28 er oppfylt.

- Øvelse 2

Bestemme om tallet 38 er perfekt eller ikke.

Løsning

Antallet blir dekomponert i de viktigste faktorene:

39 | 3
13 | 13
01 | 1

Delerne på 39 uten å inkludere selve tallet er: 1, 3 og 13. Summen 1 + 3 + 13 = 4 + 13 = 17 er ikke lik 39, derfor er 39 et ufullkommen eller ikke-perfekt tall. 

- Øvelse 3

Finn ut om nummer 120 er perfekt eller ufullkommen.

Løsning

Vi fortsetter å dekomponere tallet i dets viktigste faktorer:

120 | 2
060 | 2
 30 | 2
 15 | 3
  5 | 5
  1 | 1

Fra de viktigste faktorene fortsetter vi med å finne skillelinjene:

1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 og 120

Hvis 120 var perfekte, skulle tillegging av alle delene få 2 x 120 = 240. 

1 + 2 + 3 + 4 + 5 + 6 + 8 + 10 + 12 + 15 + 20 + 24 + 30 + 40 + 60 + 120 = 360

Dette resultatet er klart forskjellig fra 240, så det konkluderes med at tallet 120 ikke er et perfekt tall..

- Øvelse 4

Bekreft at tallet 496, oppnådd etter Euclids kriterium, er et perfekt tall.

Løsning

Tallet 496 er spaltet i sine viktigste faktorer:

496 | 2
248 | 2
124 | 2
062 | 2
031 | 31
001 | 1

Så dens delere er:

1, 2, 4, 8, 16, 31, 62, 124, 248, 496

Nå er alle lagt til, unntatt 496:

1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496

Bekrefter at det virkelig er et perfekt tall.

Referanser

1. Baldor, A. 1986. Aritmetikk. Codex-utgaver og distribusjoner.
2. Alt om primtall. Vennlige tall. Gjenopprettet fra: numeroprimos.org.
3. Wolfram MathWorld. Eulers regel. Gjenopprettet fra: mathworld.wolfram.com.
4. Wolfram MathWorld. Perfekt nummer. Gjenopprettet fra: mathworld.wolfram.com.
5. Wikipedia. Perfekte tall. Gjenopprettet fra: en.wikipedia.org.
6. Wikipedia. Vennlige tall. Gjenopprettet fra: es.wikipedia.org.