De rasjonelle tall er alle tall som kan oppnås som inndelingen av to hele tall. Eksempler på rasjonelle tall er: 3/4, 8/5, -16/3 og de som vises i følgende figur. I et rasjonelt tall er kvotienten angitt, og det er mulig å gjøre det senere om nødvendig.
Figuren representerer ethvert objekt, rundt for enkelhets skyld. Hvis vi vil dele den i to like store deler, som til høyre, har vi to halvdeler igjen, og hver er verdt 1/2.
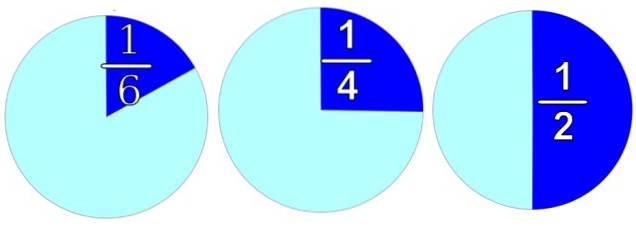
Ved å dele den i 4 like deler, får vi 4 stykker, og hver er verdt 1/4, som på bildet i midten. Og hvis det er nødvendig å distribuere den i 6 like deler, fordi hver del ville være verdt 1/6, som vi ser på bildet til venstre.
Selvfølgelig kunne vi også dele den i to ulike deler, for eksempel kunne vi beholde 3/4 deler og spare 1/4 del. Andre divisjoner er også mulig, for eksempel 4/6 deler og 2/6 deler. Det viktige er at summen av alle delene er 1.
På denne måten er det tydelig at ting som mat, penger, land og alle slags gjenstander kan deles, telles og fordeles i brøkdeler med rasjonelle tall. Og dermed utvides mengden operasjoner som kan gjøres med tallene.
Rasjonelle tall kan også uttrykkes i desimalform, som det kan sees i følgende eksempler:
1/2 = 0,5
1/3 = 0,33333 ...
3/4 = 0,75
1/7 = 0.142857142857142857…
Senere vil vi indikere hvordan man kan gå fra ett skjema til et annet med eksempler.
Artikkelindeks
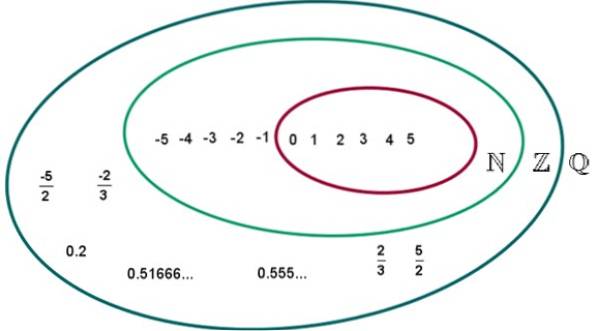
Rasjonelle tall, hvis sett vi vil betegne med bokstaven Q, har følgende egenskaper:
-Q inkluderer de naturlige tallene N og hele tallene Z.
Tatt i betraktning at et hvilket som helst tall til Det kan uttrykkes som kvotienten mellom seg selv og 1, det er lett å se at det blant de rasjonelle tallene også er naturlige tall og heltall.
Dermed kan det naturlige tallet 3 skrives som en brøkdel, og også -5:
3 = 3/1
-5 = -5/1 = 5 / -1 = - (5/1)
På denne måten er Q et numerisk sett som inkluderer et større antall tall, noe som er veldig nødvendig, siden de "runde" tallene ikke er nok til å beskrive alle mulige operasjoner å gjøre..
-Rasjonelle tall kan legges til, trekkes fra, multipliseres og deles, resultatet av operasjonen er et rasjonelt tall: 1/2 + 1/5 = 7/10; 1/2 - 1/5 = 3/10; (1/2) x (1/5) = 1/10; (1/2) ÷ (1/5) = 5/2.
-Mellom hvert par rasjonelle tall kan alltid et annet rasjonelt tall bli funnet. Faktisk er det uendelige rasjonelle tall mellom to rasjonelle tall.
Mellom rasjonellene 1/4 og 1/2 er for eksempel rasjonellene 3/10, 7/20, 2/5 (og mange flere), som kan bekreftes ved å uttrykke dem som desimaler.
-Ethvert rasjonelt tall kan uttrykkes som: i) et heltall eller ii) en begrenset (streng) eller periodisk desimal: 4/2 = 2; 1/4 = 0,25; 1/6 = 0,166666666…
-Det samme tallet kan representeres av uendelige ekvivalente brøker, og alle tilhører Q. La oss se denne gruppen:
De representerer alle desimalet 0,428571 ...
-Av alle de tilsvarende brøkene som representerer det samme tallet, er den irredusible brøkdelen, den enkleste av alle, den kanonisk representant av det nummeret. Den kanoniske representanten for eksemplet ovenfor er 3/7.
-Riktige brøker, de der telleren er mindre enn nevneren:
-Feil brøker, hvis teller er større enn nevneren:
-Naturlige tall og hele tall:
-Tilsvarende brøker:
Når telleren deles med nevneren, blir desimalformen til det rasjonelle tallet funnet. For eksempel:
2/5 = 0,4
3/8 = 0,375
1/9 = 0.11111 ...
6/11 = 0.545454 ...
I de to første eksemplene er antall desimaler begrenset. Dette betyr at når divisjonen er ferdig, får vi endelig en rest på 0.
På den annen side, i de neste to, er antallet desimaler uendelig, og det er derfor ellipsen plasseres. I sistnevnte tilfelle er det et mønster i desimalene. Når det gjelder brøkdelen 1/9, gjentas tallet 1 på ubestemt tid, mens det i 6/11 er 54.
Når dette skjer, sies desimalt å være periodisk og betegnes av en innskudd som dette:
Hvis det er en begrenset desimal, elimineres kommaet ganske enkelt, og nevneren blir enheten etterfulgt av så mange nuller som det er tall i desimalen. For eksempel, for å transformere desimal 1,26 til en brøkdel, skriv den slik:
1,26 = 126/100
Da blir den resulterende brøkdelen forenklet maksimalt:
126/100 = 63/50
Hvis desimalen er ubegrenset, blir perioden først identifisert. Deretter følges disse trinnene for å finne den resulterende brøkdelen:
-Telleren er subtraksjonen mellom tallet (uten komma eller tegneserie) og delen som bærer ikke den circumflex aksenten.
-Nevneren er et heltall med så mange 9 som det er figurer under omkretsen, og så mange 0 som det er figurer i desimaldelen det er som ikke er under omkrets.
La oss følge denne prosedyren for å transformere desimaltallet 0.428428428 ... til en brøkdel.
-Først identifiseres perioden, som er sekvensen som gjentas: 428.
-Deretter gjøres operasjonen med å trekke tallet uten komma eller aksent: 0428 fra den delen som ikke har en omkrets, som er 0. Det er altså 428 - 0 = 428.
-Nevneren er konstruert, vel vitende om at under circumflex er det 3 figurer og alle er under circumflex. Derfor er nevneren 999.
-Til slutt dannes fraksjonen og forenkles om mulig:
0,428 = 428/999
Det er ikke mulig å forenkle mer.
Når brøkene har samme nevner, er det veldig enkelt å legge til og / eller trekke dem, fordi tellerne rett og slett legges til algebraisk, og etterlater det samme som tilleggene som nevner for resultatet. Til slutt, hvis mulig, er det forenklet.
Gjør følgende algebraisk tillegg og forenkle resultatet:
Den resulterende brøkdelen er allerede ikke reduserbar.
I dette tilfellet blir tilleggene erstattet av ekvivalente brøker med samme nevner, og deretter følges prosedyren som allerede er beskrevet.
Legg til algebraisk følgende rasjonelle tall, forenkle resultatet:
Trinnene er:
-Bestem det minst vanlige multiple (LCM) av nevnerne 5, 8 og 3:
lcm (5,8,3) = 120
Dette vil være nevneren for den resulterende brøkdelen uten å forenkle.
-For hver brøk: del LCM med nevneren og multipliser med telleren. Resultatet av denne operasjonen er plassert, med dens respektive tegn, i telleren til brøkdelen. På denne måten oppnås en brøkdel som tilsvarer originalen, men med LCM som nevner..
For eksempel, for den første brøkdelen, er telleren konstruert slik: (120/5) x 4 = 96 og vi får:
Fortsett på samme måte for de resterende brøkene:
Til slutt erstattes de tilsvarende brøkene uten å glemme tegnet, og den algebraiske summen av tellerne blir utført:
(4/5) + (14/8) - (11/3) + 2 = (96/120) + (210/120) - (440/120) + (240/120) =
= (96 + 210-440 + 24) / 120 = -110 / 120 = -11/12
Multiplikasjon og deling gjøres etter reglene vist nedenfor:
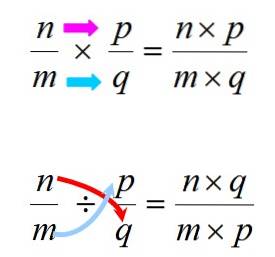
I alle fall er det viktig å huske at multiplikasjon er kommutativ, noe som betyr at rekkefølgen på faktorene ikke endrer produktet. Dette skjer ikke med deling, så det må tas hensyn til å respektere rekkefølgen mellom utbytte og divisor.
Utfør følgende operasjoner og forenkle resultatet:
a) (5/3) x (8/15)
b) (-4/5) ÷ (2/9)
(5/3) x (8/15) = (5 x 8) / (3 x 15) = 15/120 = 1/8
(-4/5) ÷ (2/9) = (-4 x 9) / (5 x 2) = -36 / 10 = -18/5
Luisa hadde $ 45. Han brukte en tidel av det på å kjøpe en bok og 2/5 av det som var igjen på en t-skjorte. Hvor mye penger har Luisa igjen? Uttrykk resultatet som en irredusibel brøk.
Boken kostet (1/10) x $ 45 = 0,1 x $ 45 = $ 4,5
Derfor satt Luisa igjen med:
45 - 4,5 $ = 40,5 $
Med de pengene gikk Luisa til klesbutikken og kjøpte skjorten, og prisen er:
(2/5) x $ 40,5 = $ 16,2
Nå har Luisa i sin portefølje:
40,5 - 16,2 $ = 24,3 $
For å uttrykke det som en brøkdel, skrives det slik:
24,3 = 243/10
Det er ikke reduserbart.
Ingen har kommentert denne artikkelen ennå.