De reelle tall de utgjør det numeriske settet som inkluderer de naturlige tallene, heltallene, det rasjonelle og det irrasjonelle. De er betegnet med symbolet ℝ eller ganske enkelt R og omfanget de har innen vitenskap, ingeniørfag og økonomi er slik at når man snakker om "tall", blir det nesten tatt for gitt at det er et reelt tall.
Virkelige tall har blitt brukt siden antikken, selv om de ikke fikk det navnet. Allerede fra den tiden Pythagoras utviklet sin berømte setning, oppstod tall som ikke kunne oppnås som kvotienter med naturlige tall eller heltall.
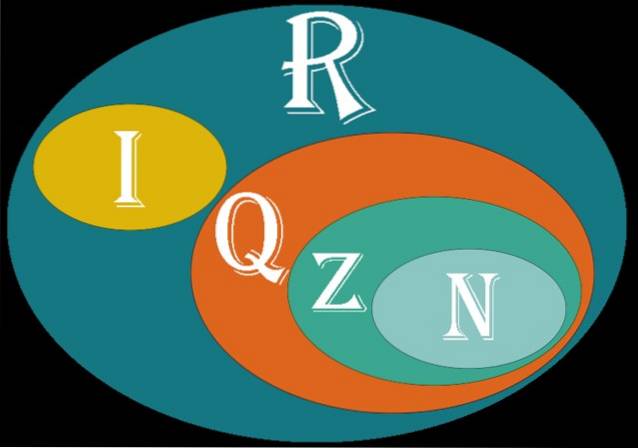
Eksempler på tall er √2, √3 og π. Disse tallene kalles irrasjonell, i motsetning til rasjonelle tall, som kommer fra heltall. Det var derfor nødvendig med et numerisk sett som omfatter begge klasser av tall..
Begrepet "reelt tall" ble opprettet av den store matematikeren René Descartes (1596-1650), for å skille mellom de to slags røtter som kan oppstå ved å løse en polynomligning.
Noen av disse røttene kan være jevne røtter med negative tall, Descartes kalte disse "imaginære tall" og de som ikke var, var reelle tall.
Benevnelsen vedvarte over tid, og ga opphav til to store numeriske sett: reelle tall og komplekse tall, et større sett som inkluderer reelle tall, imaginære tall og de som er del reelle og delvis imaginære..
Utviklingen av reelle tall fortsatte sin gang til i 1872 definerte matematikeren Richard Dedekind (1831-1936) formelt sett med reelle tall gjennom den såkalte kutt av Dedekind. Syntesen av arbeidet hans ble publisert i en artikkel som så lyset samme år.
Artikkelindeks
Tabellen nedenfor viser eksempler på reelle tall. Dette settet har som delmengder de naturlige tallene, heltallene, det rasjonelle og det irrasjonelle. Ethvert antall av disse settene er i seg selv et reelt tall.
Derfor 0, negative, positive, brøker og desimaler er reelle tall.
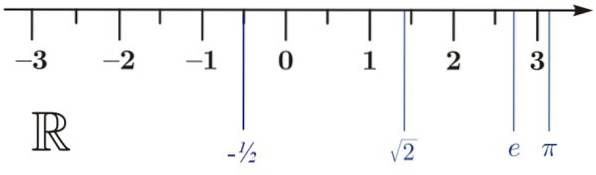
Reelle tall kan vises på den virkelige linjen R, som bildet viser. Det er ikke nødvendig at 0 alltid er til stede, men det er praktisk å vite at til venstre er de negative realene og til høyre de positive. Det er derfor det er et utmerket referansepunkt.
På den virkelige linjen blir det tatt en skala der heltallene er funnet:… 3, -2, -1, 1, 2, 3…. Pilen indikerer at linjen strekker seg til uendelig. Men det er ikke alt, uansett intervall, vil vi også alltid finne uendelige reelle tall.
De reelle tallene er representert i rekkefølge. Til å begynne med er det rekkefølgen på heltallene, der positive alltid er større enn 0, mens negativene er mindre..
Denne ordren holdes innenfor de reelle tallene. Følgende ulikheter er vist som et eksempel:
a) -1/2 < √2
b) e < π
c) π> -1/2
-Virkelige tall inkluderer naturlige tall, heltall, rasjonelle tall og irrasjonelle tall..
-Den kommutative egenskapen til tillegg er oppfylt: rekkefølgen til tilleggene endrer ikke summen. Hvis a og b er to reelle tall, er det alltid sant at:
a + b = b + a
-0 er det nøytrale elementet i summen: a + 0 = a
-For summen er den tilknyttede eiendommen tilfredsstilt. Hvis a, b og c er reelle tall: (a + b) + c = a + (b + c).
-Det motsatte av et reelt tall til er -a.
-Subtraksjon er definert som summen av det motsatte: a - b = a + (-b).
-Produktets kommutative egenskap er tilfredsstilt: rekkefølgen på faktorene endrer ikke produktet: a.b = b.a
-I produktet brukes den assosiative egenskapen også: (a.b) .c = a. (B.c)
-1 er det nøytrale elementet i multiplikasjonen: a.1 = a
-Den fordelende egenskapen til multiplikasjon med hensyn til tillegg er gyldig: a. (b + c) = a.b + a.c
-Divisjon med 0 er udefinert.
-Ethvert reelt tall a, unntatt 0, har multiplikativ invers av-1 slik at a.a-1 = 1.
-Hvis a er et reelt tall: a0 = 1 og a1 = a.
-Den absolutte verdien eller modulen til et reelt tall er avstanden mellom tallet og 0.
Med de reelle tallene kan du utføre operasjonene som gjøres med de andre numeriske settene, inkludert addisjon, subtraksjon, multiplikasjon, divisjon, empowerment, radication, logaritmer og mer.
Deling av 0 er som alltid ikke definert, verken negative logaritmer av tall eller 0, selv om det er sant at log 1 = 0 og at logaritmer av tall mellom 0 og 1 er negative.
Anvendelsen av reelle tall på alle slags situasjoner er ekstremt variert. Reelle tall fremstår som svar på mange problemer innen eksakt vitenskap, informatikk, ingeniørfag, økonomi og samfunnsvitenskap..
Alle slags størrelser og størrelser som avstander, tider, krefter, lydintensitet, penger og mange flere, har sitt uttrykk i reelle tall.
Overføring av telefonsignaler, bildet og lyden av en video, temperaturen på et klimaanlegg, et varmeapparat eller et kjøleskap kan styres digitalt, noe som betyr å transformere fysiske størrelser til numeriske sekvenser.
Det samme skjer når du foretar en banktransaksjon over Internett eller konsulterer direktemeldinger. De virkelige tallene er overalt.
Vi kommer til å se med øvelser hvordan disse tallene fungerer i vanlige situasjoner som vi møter på daglig basis..
Postkontoret godtar kun pakker der lengden, pluss omkretsmålingen, ikke overstiger 108 tommer. For at den viste pakken skal aksepteres, må det derfor oppfylles at:
L + 2 (x + y) ≤ 108
a) Kommer en pakke som måler 6 tommer bred, 8 tommer høy og 5 fot lang gjennom??
b) Hva med en som måler 2 x 2 x 4 fot3?
c) Hva er den høyeste akseptable høyden for en pakke hvis base er firkantet og måler 9 x 9 inchesto?
L = 5 fot = 60 tommer
x = 6 tommer
y = 8 tommer
Operasjonen å løse er:
L + 2 (x + y) = 60 + 2 (6 + 8) tommer = 60 + 2 x 14 tommer = 60 + 28 tommer = 88 tommer
Pakken aksepteres.
Dimensjonene på denne pakken er mindre enn pakke a), så de klarer begge å passere.
I denne pakken:
x = L = 9 tommer
Det må oppfylles at:
9+ 2 (9 + y) ≤ 108
27 + 2y ≤ 108
2 år ≤ 81
og ≤ 40,5 tommer
Ingen har kommentert denne artikkelen ennå.