
Utviklet notasjon hva det er, eksempler og øvelser
De utvidet notasjon er en der en numerisk figur uttrykkes som en sum der posisjonsverdien til hvert siffer som utgjør tallet blir tatt i betraktning.
For eksempel, når du skriver et tall som 2345, har hvert siffer i det et posisjonelt hierarki. Når du leser fra det ytterste høyre sifferet til venstre, vokser hierarkiet eller verdien.
I tallet 2345 representerer sifferet 5 enheter, sifferet 4 representerer fire tiere, 3 tilsvarer den tredje posisjonen fra venstre til høyre og derfor representerer 3 tre hundre, til slutt representerer 2 to tusen. Med andre ord, i utviklet eller utvidet notasjon, er figuren 2345 skrevet slik:
2345 = 2 tusen + 3 hundre + 4 tiere + 5 en
Men det kan også uttrykkes som følger:
2345 = 2 x 1000 + 3 x 100 + 4 x 10 + 5 x 1.
Også figur 2345 kan skrives som summen av krefter på 10:
2345 = 2 x 10 ^ 3 + 3 x 10 ^ 2 + 4 x 10 ^ 1 + 5 x 10 ^ 0
Hvor circumflex ^ betyr å heve til den angitte eksponenten. For eksempel 10 ^ 3 = 10 x 10 x 10 = 1000. En annen måte å skrive eksponentene på er ved å bruke et overskrift:
2345 = 2 x 103 + 3 x 10to + 4 x 101 + 5x100
Artikkelindeks
- 1 Posisjonsnummereringssystem
- 1.1 Brøk- eller desimaltall
- 2 Eksempler på utvidet notasjon
- 2.1 Eksempel 1
- 2.2 Eksempel 2
- 3 Øvelser med utvidet notasjon
- 3.1 Øvelse 1
- 3.2 Øvelse 2
- 3.3 Øvelse 3
- 3.4 Øvelse 6
- 4 Referanser
Posisjonsnummereringssystem
Det arabiske tallsystemet er tallene som brukes daglig i de aller fleste verdensdeler og land. Arabiske tall er et basissystem 10 fordi ti symboler eller grafemer brukes til å skrive et hvilket som helst tall. Disse ti symbolene er:
0 1 2 3 4 5 6 7 8 9
Med bare ett av disse symbolene kan tall fra null til ni uttrykkes. For å uttrykke tall som er større enn ni, brukes posisjonssystemet i base ti. Tallet 10 er ti og null enheter. Tallet 11 er en ti og en enhet. Tallet 123 (hundre og tjuetre) er hundre, to tiere og tre. Skrevet i form av krefter på ti vil tallet 123 være:
1 × 10 ^ 2 + 2 × 10 ^ 1 + 3 × 10 ^ 0
Hvor:
10 ^ 2 = 10 x 10 = 100
10 ^ 1 = 10
10 ^ 0 = 1.
Med dette eksemplet er det tydelig at posisjonen til sifferet helt til høyre er posisjon 0 og representerer antall enheter, at det andre sifferet fra høyre til venstre er posisjon 1 og representerer antall tiere, det tredje sifferet (fra høyre venstre) har posisjon 2 og representerer hundrevis.
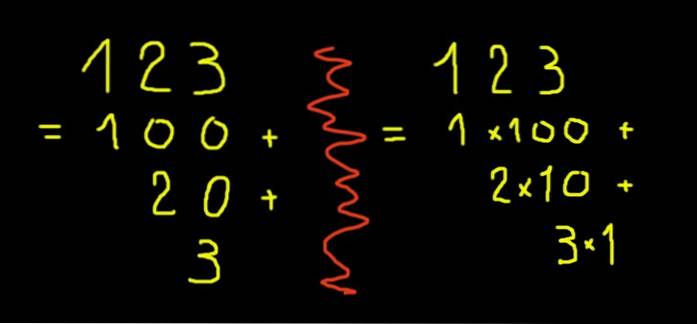
Brøk- eller desimaltall
Med desimalposisjonssystemet er det også mulig å representere tall eller figurer som er mindre enn enheten eller som er større enn enheten, men ikke heltall, det vil si at de har brøkdeler av enheten.
For å representere i det arabiske desimalsystemet er brøkdelen ½, det vil si halvparten av enheten, skrevet:
½ = 0,5
For å komme til dette uttrykket i vårt base 10-system, er følgende operasjoner implisitt utført:
1- Telleren og nevneren multipliseres med 5 for å ha den tilsvarende brøkdelen 5/10 = 1/2.
2- Deling av 10 tilsvarer å multiplisere med kraften i base ti med eksponent minus en (10 ^ -1), det vil si 5/10 = 5 × 10 ^ -1.
3- Den negative eksponenten indikerer hvor mange ganger det angitte tallet flyttes eller plasseres til høyre fra enhetens posisjon, i vårt tilfelle ville det være 0,5.
4- ½ = 0,5 i utvidet notasjon er skrevet slik:
0,5 = 0x10 ^ 0 + 5 × 10 ^ -1
Hvor 10 ^ -1 = 0,1 er en tidel (brøkdelen som tilsvarer enheten delt i 10 like deler).
På denne måten tilsvarer tallet 0,5 fem tideler, men tallet 0,05 tilsvarer 5 hundredeler og 0,005 til 5 tusendeler.
Eksempler på utvidet notasjon
Eksempel 1
Gitt tallet 40201 i standardnotasjon, konverter det til utvidet notasjon.
Løsning:
4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1 = 40201
Eksempel 2
Skriv brøken ¾ i utvidet notasjon.
Løsning:
I dette tilfellet har du tre fjerdedeler av enheten.
3/4 = 15/20 = 75/100 = 0,75 = 7/10 + 5/100 =
7 × 10 ^ -1 + 5 × 10 ^ -2.
Sagt med ord vil det se slik ut:
Brøken ¾ tilsvarer syv tideler pluss fem hundredeler.
Øvelser med utvidet notasjon
Øvelse 1
Si med ord det utvidede uttrykket til figuren 40201 fra eksempel 1.
Løsning:
Den utviklede notasjonen ser slik ut:
40201 = 4 × 10000 + 0x1000 + 2 × 100 + 0x10 + 1 × 1
At det på ordspråket blir sagt:
Fire titusener, pluss null tusen, pluss to hundre, pluss null titalls, pluss en enhet.
Øvelse 2
Uttrykk forrige figur med ord og del ned den tilsvarende setningen i utvidet form.
Løsning:
Figuren 40201 i ord uttrykkes slik:
Førti tusen to hundre en
Forrige setning kan utvikles som:
40 × 1000 + 2 × 100 + 1
Det kan sies at måten å uttale figurene på er en halvutviklet måte å uttrykke dem på.
Øvelse 3
Skriv i utvidet form tallet 7/3.
Løsning:
Det er en figur uttrykt som en upassende brøkdel, siden telleren er større enn nevneren, er tallet større enn enheten.
Denne feilaktige brøkdel kan dekomponeres som summen av brøkene 6/3 + 1/3. Den første av brøkene resulterer i et heltall 2, mens 1/3 = 0,3333333, der siffer 3 gjentas på ubestemt tid. Så det utvidede desimaluttrykket til figur 7/3 vil alltid være et omtrentlig uttrykk:
7/3 = 2 + 1/3 ≃ 2 + 0,333 = 2 + 3 × 10 ^ -1 + 3 × 10 ^ -2 + 3 × 10 ^ -3.
Øvelse 6
Skriv i standardnotasjon og deretter i utvidet form nummeret: Tjuetre milliarder to hundre og femti millioner fem hundre tjuetusen tre hundre tjuefem og tre tjuetre tusendeler.
Løsning:
Det skal huskes at en milliarder tilsvarer en milliard. Ordet milliarder det ble akseptert av det kongelige spanske akademiet i 1995 på forespørsel fra den avdøde Venezuelas president Rafael Caldera, et medlem av det venezuelanske språkakademiet. I så fall er figuren for øvelsen i standardnotasjon skrevet slik:
23,2501526,325,023
23 milliarder + 250 millioner + 526 tusen + 325 enheter + 23 tusendeler.
23 × 10 ^ 9 + 250 × 10 ^ 6 + 526 × 10 ^ 3 + 325 × 10 ^ 0 + 23 × 10 ^ -3
Til slutt er figuren skrevet i utvidet notasjon:
2 × 10 ^ 10 + 3 × 10 ^ 9 + 2 × 10 ^ 8 + 5 × 10 ^ 7 + 0x10 ^ 6 + 5 × 10 ^ 5 + 2 × 10 ^ 4 + 6 × 10 ^ 3 + 3 × 10 ^ 2 + 2 × 10 ^ 1 + 5 × 10 ^ 0 + 0x10 ^ -1 + 2 × 10 ^ -2 + 3 × 10 ^ -3.
Referanser
- Khan Academy. Plasser verdidiagrammer. Gjenopprettet fra: es.khanacademy.org
- Khan Academy. Skriv et nummer i utvidet form (video). Gjenopprettet fra: es.khanacademy.org
- Ifrah, Geoges (1998): Universell historie om figurer. Espasa Calpe S.A.
- Wikipedia. Posisjonsnotasjon. Gjenopprettet fra: es.wikipedia.com
- Wikipedia. Milliarder. Gjenopprettet fra: es.wikipedia.com


Ingen har kommentert denne artikkelen ennå.